Bijlage 2. Afleiding parameter K
De onderstaande afleiding is gebaseerd op een soortgelijke afleiding uit het rapport “Herziening gewichtenregeling primair onderwijs – Fase 3: bijschatting voor niet-ingeschreven leerlingen”.
Noteer de onderwijsscore van leerling i als yi. Een algemene formule voor de achterstandsscore zonder drempel van school j met een populatie van bekostigde leerlingen Uj is gegeven door:
$$S_{j}(q) = \sum_{i \in U_{j}}^{}{I\left\{ y_{i} \leq y_{L}(q) \right\}\left( y_{ref} - y_{i} \right)}. \tag{1}$$
Hierbij is yref een referentiescore en yL (q) de score die hoort bij het q × 100%-percentiel van de verdeling van onderwijsscores. Verder is I{.} een indicatorfunctie die gelijk is aan 1 als het argument waar is en anders gelijk aan 0. De achterstandsscore (zonder drempel) waarmee in de praktijk wordt gewerkt is een speciaal geval van (1) met q = 0,15 en \(y_{ref} = \overline{y}\) (het landelijke gemiddelde).
In het vervolg nemen we ter vereenvoudiging aan dat de populatie leerlingen bestaat uit M strata, waarbij de bijdrage van een leerling aan de variantie van de achterstandsscore constant is per stratum. We stellen voor om in de praktijk de volgende M = 7 strata te onderscheiden:
| Stratum | Omschrijving |
|---|---|
| 1 | opleidingsniveau van beide ouders onbekend, onderwijsscore direct bepaald |
| 2 | opleidingsniveau van beide ouders onbekend, onderwijsscore geïmputeerd |
| 3 | opleidingsniveau alleen van moeder bekend, onderwijsscore direct bepaald |
| 4 | opleidingsniveau alleen van moeder bekend, onderwijsscore geïmputeerd |
| 5 | opleidingsniveau alleen van vader bekend, onderwijsscore direct bepaald |
| 6 | opleidingsniveau alleen van vader bekend, onderwijsscore geïmputeerd |
| 7 | opleidingsniveau van beide ouders bekend, onderwijsscore direct bepaald óf leerling komt voor in een bestand van COA of IND |
De reden om voor deze indeling in strata te kiezen is dat de hoeveelheid beschikbare informatie per stratum verschilt, wat mogelijk leidt tot verschillende bijdragen per stratum aan de variantie van de achterstandsscore op schoolniveau. Voor leerlingen die voorkomen in de registraties van het COA en de IND wordt een vaste score geïmputeerd: hun variantiebijdrage is daarom praktisch nul. Dit laatste hebben zij gemeenschappelijk met alle kinderen voor wie van beide ouders het opleidingsniveau bekend is; vandaar dat deze twee deelpopulaties zijn samengenomen tot één stratum. De overige strata komen overeen met een indeling die is gebruikt in de Jaarlijkse monitor Risico-indicator onderwijsachterstanden Primair Onderwijs.
We noteren de fractie leerlingen
op school j die behoren tot stratum g als pjg, met 0 ≤ pjg ≤ 1 (g = 1,…,7). Per definitie geldt: pj1 + pj2 + pj3 + pj4 + pj5 + pj6 + pj7 = 1 voor elke school.
Stel dat de achterstandsscore zonder drempel Sj = Sj (q) voor school j met nj bekostigde leerlingen (of algemener: een groep van nj kinderen) twee keer onafhankelijk zou worden berekend op basis van dezelfde brongegevens, met als resultaat de scores Sj1 en Sj2. Omdat de twee scores onafhankelijk van elkaar zijn7), geldt voor de variantie van het verschil Sj2 -Sj1:
$${var}\left( S_{j2} - S_{j1} \right) = {var}\left( S_{j1} \right) + {var}\left( S_{j2} \right) = 2{var}\left( S_{j} \right).$$
Dat wil zeggen:
$${var}\left( S_{j} \right) = \frac{{var}\left( S_{j2} - S_{j1} \right)}{2}. \tag{2}$$
Een formule voor var(Sj) kan daarom worden afgeleid uit een formule voor var(Sj2 - Sj1).
Bij de twee onafhankelijke berekeningen horen strikt genomen ook aparte waarden voor de grootheden yref, yL (q) en (bij scores met drempel) yref,L (q). Zeg: yref,1, yL,1 (q) bij de eerste berekening en yref,2, yL,2 (q) bij de tweede berekening. De variatie in deze grootheden is echter veel kleiner dan die in de achterstandsscores per school, omdat ze worden geschat uit de volledige populatie (meer dan een miljoen leerlingen). We kunnen de stochastiek in deze grootheden daarom verwaarlozen en we zullen ze hieronder behandelen als constanten.
De twee achterstandsscores Sj1 en Sj2 zijn gebaseerd op onafhankelijk van elkaar berekende individuele onderwijsscores. Noteer deze onderwijsscores voor leerling i als yi1 en yi2. Volgens formule (1) is Sj2 - Sj1 voor een school met leerlingenpopulatie Uj te schrijven als:
$$S_{j2} - S_{j1} = \sum_{i \in U_{j}}^{}\left\lbrack I\left\{ y_{i2} \leq y_{L,2}(q) \right\}\left( y_{ref,2} - y_{i2} \right) - I\left\{ y_{i1} \leq y_{L,1}(q) \right\}\left( y_{ref,1} - y_{i1} \right) \right\rbrack \equiv \sum_{i \in U_{j}}^{}z_{i}$$
Beschouw eerst de situatie dat een school uitsluitend leerlingen heeft die zijn ingeschreven in één bepaald stratum. Op basis van hun onderwijsscores yi1 en yi2 kunnen deze leerlingen worden verdeeld in vier groepen, elk met een eigen bijdrage zi aan het verschil Sj2 - Sj1:
yi2 ≥ yL,2 (q) yi2 < yL,2 (q)
yi1 ≥ yL,1 (q) groep W groep X
bijdrage: zi = 0 bijdrage: zi = yref,2 - yi2
yi1 < yL,1 (q) groep Y groep Z
bijdrage: zi = yi1 - yref,1 bijdrage: zi = yi1 - yi2
Voor leerlingen in groep W vallen beide realisaties van de onderwijsscore boven de ondergrens yL (q). De bijdragen van deze leerlingen aan Sj1 en Sj2 zijn beide gelijk aan nul. Voor leerlingen in groep X en Y valt een van beide onderwijsscores onder yL (q) en de andere erboven. De bijdrage aan Sj2 - Sj1 is daarom zi=yref,2 - yi2 (groep X) of zi=yi1 - yref,1 (groep Y). In de onderstaande afleiding is voor deze leerlingen relevant wat de gemiddelde waarde van deze bijdrage is en wat de variantie daaromheen is. Definieer:
$$\begin{align} \mu_{XY} &= E\left( y_{ref,2} - y_{i2} \middle| i \in X \right) = - E\left( y_{i1} - y_{ref,1} \middle| i \in Y \right)\\ \omega_{XY}^{2} &= {var}\left( y_{ref,2} - y_{i2} \middle| i \in X \right) = {var}\left( y_{i1} - y_{ref,1} \middle| i \in Y \right). \end{align}$$
Ter vereenvoudiging is hierbij aangenomen dat (per stratum) alle leerlingen in groep X (en Y) dezelfde verwachting en dezelfde variantie hebben. De gelijkheden E(yref,2 - yi2│i ∈ X) = - E(yi1 - yref,1)│i ∈ Y) en var(yref,2 - yi2│i ∈ X)=var(yi1 - yref,1│i ∈ Y) volgen uit symmetrie-overwegingen, aangezien beide scores yi1 en yi2 afkomstig zijn uit dezelfde verdeling.
Voor leerlingen in groep Z vallen beide onderwijsscores onder yL (q). De bijdrage aan het verschil Sj2 - Sj1 is zi = yi1 - yi2. In verwachting is dit verschil gelijk aan nul. Voor de variantie van het verschil wordt de volgende parameter ingevoerd:
$$\sigma_{Z}^{2} = {var}\left( y_{i1} - y_{i2} \middle| i \in Z \right)$$
Ook hier is de vereenvoudigende aanname gemaakt dat deze variantie (per stratum) voor alle leerlingen in groep Z gelijk is. Definieer ten slotte de kans dat een willekeurig gekozen leerling in groep V valt als πV (met V ∈ {W,X,Y,Z}).
De onderwijsscores zijn bij benadering onafhankelijk tussen verschillende leerlingen. (De gebruikte imputatiemethoden introduceren enige afhankelijkheid tussen de scores, maar deze kan worden verwaarloosd.) Onder de aanname dat de onderwijsscores onafhankelijk zijn tussen leerlingen volgt:
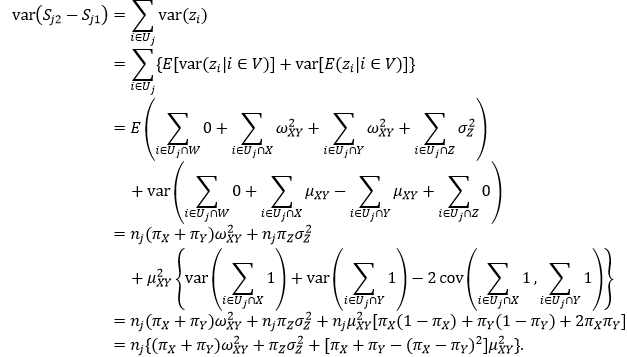
In de tweede regel is een standaard-variantiedecompositie gebruikt, waarbij in de binnenste variantie en verwachting is geconditioneerd op de groep (W, X, Y of Z) waarin leerling i valt. In de een-na-laatste regel is gebruikgemaakt van eigenschappen van een multinomiale verdeling.
Stel nu dat de school leerlingen kan bevatten uit alle strata van de populatie die hierboven zijn gedefinieerd, waarbij pjg de fractie leerlingen uit stratum g aanduidt. Per stratum hebben de geïmputeerde scores mogelijk andere eigenschappen. Daarom moeten aparte parameters worden ingevoerd per stratum. De kans dat een willekeurig gekozen leerling uit stratum g in groep V valt wordt genoteerd als πVg (V ∈ {W,X,Y,Z}). Definieer verder:
$$\begin{align}
\mu_{XYg} &= E\left( y_{ref,2} - y_{i2} \middle| i \in X,g \right) = - E\left( y_{i1} - y_{ref,1} \middle| i \in Y,g \right),\\
\omega_{XYg}^{2} &= {var}\left( y_{ref,2} - y_{i2} \middle| i \in X,g \right) = {var}\left( y_{i1} - y_{ref,1} \middle| i \in Y,g \right),\\
\sigma_{Zg}^{2} &= {var}\left( y_{i1} - y_{i2} \middle| i \in Z,g \right).
\end{align}$$
Analoog aan het voorafgaande kan voor de variantie van Sj2 - Sj1 bij een school met pjg nj leerlingen uit stratum g worden afgeleid dat:
$${var}\left( S_{j2} - S_{j1} \right) = n_{j}\sum_{g = 1}^{M}{p_{jg}\left\{ \left( \pi_{Xg} + \pi_{Yg} \right)\omega_{XYg}^{2} + \pi_{Zg}\sigma_{Zg}^{2} + \left\lbrack \pi_{Xg} + \pi_{Yg} - {(\pi_{Xg} - \pi_{Yg})}^{2} \right\rbrack\mu_{XYg}^{2} \right\}}.$$
Definieer:
$$K_{g} = \left( \pi_{Xg} + \pi_{Yg} \right)\omega_{XYg}^{2} + \pi_{Zg}\sigma_{Zg}^{2} + \left\lbrack \pi_{Xg} + \pi_{Yg} - {(\pi_{Xg} - \pi_{Yg})}^{2} \right\rbrack\mu_{XYg}^{2} \tag{3}$$
Uit (2) volgt nu dat
$${var}\left( S_{j} \right) = \frac{n_{j}}{2}\sum_{g = 1}^{M}{p_{jg}K_{g}}.$$
De grootheden Kg en de onderliggende parameters uit formule (3) hebben we in dit onderzoek geschat door voor de populatie van 2021 het volledige bijschattingsproces drie keer onafhankelijk uit te voeren. Dit geeft drie mogelijke paarsgewijze vergelijkingen tussen onderwijsscores: (yi1,yi2 ), (yi1,yi3 ) en (yi2,yi3 ).
8) Gelijk is de bijdrage in deze groep zi = yi1 - yi2 + yref,2 - yref,1. Zoals opgemerkt is het verschil yref,2 - yref,1 in de praktijk verwaarloosbaar klein. Het wordt hier daarom gemakshalve weggelaten.