Onderzoek herijking risico-indicator onderwijsachterstanden – fase 1
Over deze publicatie
Om onderwijsachterstanden in het primair onderwijs (po) te verminderen kent het ministerie van Onderwijs, Cultuur en Wetenschap (OCW) extra middelen toe aan scholen en gemeenten. Het ministerie verdeelt deze middelen aan de hand van de door het Centraal Bureau voor de Statistiek (CBS) ontwikkelde risico-indicator onderwijsachterstanden. Op verzoek van het ministerie doet het CBS onderzoek naar het actualiseren van het model dat voor deze indicator wordt gebruikt.
In het huidige rapport staan een vijftal vooronderzoeken centraal: het effect van het uitstellen van middeling bij het berekenen van de onderwijsscores, verbetering van de imputatiemethode van ontbrekende opleidingsniveaus, verbetering van de imputatiemethode van onderwijsscores, uniformering van eindtoetsscores en een expertraadpleging met betrekking tot relevante achtergrondkenmerken voor het ontstaan van onderwijsachterstanden.
1. Inleiding
In het huidige onderwijsachterstandenbeleid voor het primair onderwijs en het gemeentelijke onderwijsachterstandenbeleid maakt het ministerie van Onderwijs, Cultuur en Wetenschap (OCW) gebruik van de risico-indicator onderwijsachterstanden die het Centraal Bureau voor de Statistiek (CBS) eerder in opdracht van het ministerie heeft ontwikkeld1). Namelijk door het CBS met deze indicator voor alle peuters van 2,5 tot 4 jaar en alle basisschoolleerlingen een onderwijsscore te laten berekenen en die scores te laten optellen conform de Besluiten2) tot achterstandsscores per school en per gemeente. Deze drukken dan de verwachte onderwijsachterstandsproblematiek op scholen en in gemeenten uit, op basis waarvan OCW het onderwijsachterstandenbudget over de scholen en gemeenten zal verdelen. In 2019 was dit beleid voor het eerst van kracht.
Om de risico-indicator onderwijsachterstanden actueel te houden, heeft OCW te kennen gegeven de indicator regelmatig te willen evalueren. Hierdoor kunnen nieuwe ontwikkelingen mee worden genomen in de indicator. De eerste evaluatie is uitgevoerd in 2021 en betrof een beperkte herziening waarbij vooral is gekeken naar de actualisatie van de coëfficiënten en schaalwaarden van het model3). De resultaten van deze herziening zijn in 2022 voor het eerst toegepast bij het berekenen van de achterstandsscores voor scholen en in 2023 voor gemeenten. In de periode 2023 tot 2025 heeft OCW een grote evaluatie voorzien waarbij de gehele indicator tegen het licht zal worden gehouden.
Ten behoeve van de evaluatie in de periode 2023 – 2025 heeft OCW via het Nationaal Regieorgaan Onderwijsonderzoek een intelligentiemeting uit laten voeren onder een representatieve steekproef van de basisschoolleerlingen in groep 6 van het schooljaar 2020/’21. Aangevuld met de eindtoetsscores van schooljaar 2022/’23 en relevante achtergrondkenmerken van de betreffende leerlingen, kan deze intelligentiemeting vervolgens worden gebruikt om een nieuw model te ontwikkelen waarbij onderwijsachterstanden wordt geschat.
Deze evaluatie zal uit een drietal fasen bestaan. In de eerste fase staan een aantal voorbereidende onderzoeken voor het nieuw te schatten model voor onderwijsachterstanden centraal. De tweede fase zal vervolgens in het teken staan van dit nieuw te schatten model voor onderwijsachterstanden. Hierbij worden de bevindingen uit de eerste fase verwerkt in het nieuw te schatten model. In de derde fase zullen de uitkomsten van de eerste en tweede fase verwerkt worden in een gestandaardiseerde productiestatistiek. Dit rapport heeft betrekking op de eerste fase en bestaat uit vijf onderdelen.
Naast de methodologische onderzoeken over de ontwikkeling van de indicator1), heeft het CBS na de ingebruikname van de indicator in 2018 diverse plausibiliteits- en monitoringonderzoeken gepubliceerd4). In deze onderzoeken is gekeken naar de werking van de indicator over de jaren heen. Op basis van deze onderzoeken zijn een drietal verbetermogelijkheden geïdentificeerd: het uitstellen van het middelen van de onderwijsscores tot na het berekenen van de achterstandsscores, het verbeteren van het imputatiemodel voor het opleidingsniveau van de ouders en het verbeteren van het imputatiemodel voor de onderwijsscores voor kinderen in de populatie waarvoor geen onderwijsscore kan worden berekend. Deze drie verbetertrajecten zullen in de hoofstukken 2 tot en met 4 aan de orde komen. In hoofdstuk 5 onderzoeken we op welke wijze voor de diverse eindtoetsen een uniforme prestatiemaatstaf kan worden ontwikkeld. Als laatste presenteren we in hoofdstuk 6 de resultaten van een expertraadpleging naar factoren die van invloed zijn op het risico op onderwijsachterstanden.
2) Besluit van 27 augustus 2018 tot wijziging van het Besluit bekostiging WPO in verband met het aanpassen van de groeiregeling en van het onderwijsachterstandenbeleid in het primair onderwijs (Staatsblad 2018, 334), en Besluit van 27 augustus 2018, houdende regels met betrekking tot specifieke uitkeringen ten behoeve van het gemeentelijk onderwijsachterstandenbeleid (Besluit specifieke uitkeringen gemeentelijk onderwijsachterstandenbeleid) (Staatsblad 2018, 315).
3) De resultaten van dit onderzoek zijn vastgelegd in een rapport: Herziening onderwijsachterstandenindicator primair onderwijs 2021.
4) Om zicht te houden op de werking van de onderwijsachterstandenindicator publiceert het CBS jaarlijks plausibiliteitsanalyses en een monitoronderzoek. De meest recente plausibiliteitsanalyse heeft betrekking op de achterstandsscores voor gemeenten. Het laatste monitoringonderzoek heeft betrekking op de periode 2017 - 2022.
2. Uitstellen middeling onderwijsscores
2.1 Inleiding
In de huidige methodiek van de risico-indicator onderwijsachterstanden wordt het opleidingsniveau van ouders waar dit niet bekend is tien keer geïmputeerd. Vervolgens wordt voor iedere imputatieronde een onderwijsscore berekend voor alle peuters en basisschoolleerlingen van wie beide ouders bekend zijn in de Basis Registratie Personen (BRP). Direct hierna wordt er een gemiddelde onderwijsscore berekend van deze tien losse berekeningen. Dit gemiddelde wordt vervolgens in het vervolg gebruikt. Voor kinderen van wie van één of beide ouders het opleidingsniveau ontbreekt zal de gemiddelde score over tien imputatieronden vaak boven de doelgroepgrens van 15% uitkomen, ook als enkele van de tien afzonderlijke scores daar wél onder liggen. Deze kinderen wegen door deze middeling dan helemaal niet mee in de achterstandsscore op schoolniveau, terwijl de spreiding in de imputaties in feite laat zien dat ze met een bepaalde kans wel behoren bij de groep kinderen met een verwachte achterstand. Dit verschijnsel werkt ook door als deze kinderen vervolgens als donor worden gebruikt voor het imputeren van scores voor kinderen met onbekende ouders. Dit kan worden voorkomen door de scores uit de tien imputatieronden zo lang mogelijk afzonderlijk te behandelen en pas te middelen nadat de scores zijn geaggregeerd naar school- of gemeenteniveau. In dit deelonderzoek zullen de effecten van deze aanpassing op de achterstandsscores van scholen en gemeenten daarom geïsoleerd worden bekeken.
2.2 Data en methoden
Voor dit onderzoek hebben we gebruik gemaakt van de microdatabestanden van de risico-indicator onderwijsachterstanden voor de jaren 2019, 2020 en 2021. Met behulp van deze data vergelijken we de huidige methode met een methode waarbij de middeling pas aan het einde van het proces wordt toegepast. Vanaf het berekenen van de onderwijsscores verloopt het huidige proces globaal als volgt:
- Voor elk kind worden 10 onderwijsscores berekend.
- Vervolgens wordt het gemiddelde over deze 10 scores berekend.
- Daarna worden ontbrekende waardes voor dit gemiddelde geïmputeerd.
- Tenslotte wordt er per school of gemeente één achterstandsscore berekend over deze gemiddelde score.
Door de middeling zo laat mogelijk toe te passen verandert het proces als volgt:
- Voor elk kind worden 10 onderwijsscores berekend.
- Vervolgens worden voor elk van deze 10 scores ontbrekende waardes geïmputeerd.
- Daarna worden er 10 achterstandsscores berekend op basis van de 10 onderwijsscores.
- Tenslotte worden deze achterstandsscores gemiddeld per school of gemeente.
Zoals te lezen in het vierde methoderapport, was de verwachting dat het uitstellen van de middeling zou leiden tot een verbetering van de scores doordat bij het imputeren per kind en per ronde een andere imputatiedonor gekozen kan worden. Dit zou moeten leiden tot een robuustere schatting van de onderwijsscore, en als resultaat ook de achterstandsscore, met name voor kinderen van wie het opleidingsniveau van beide ouders onbekend is. Dit is ook de verwachting omdat de spreiding van achterstandsscores bij deze groep relatief groot is, waardoor het relatief vaak voor kan komen dat het gemiddelde van 10 imputatierondes boven de grenswaarde van 15% ligt terwijl deze voor een deel van de individuele scores eronder ligt. Dit betekent in feite dat er een kans is dat ze bij de groep met een verwachte achterstand horen. Bij de oude methode wegen deze kinderen helemaal niet mee in het berekenen van achterstandsscores op schoolniveaus. Wanneer middeling wordt uitgesteld, wegen deze leerlingen wel mee in rondes waarin hun scores onder de grenswaarde liggen. Zo wordt de kans dat ze onder de grenswaarde liggen toch meegenomen in de uiteindelijke berekening van de achterstandsscores. De methodes werden met elkaar vergeleken voor drie jaren: 2019, 2020 en 2021. Ze zijn vergeleken op verschillende aspecten.
Stabiliteit. Als verschillen in onderwijsscores jaar op jaar kleiner zijn, dan is dat een indicatie dat er minder ruis in de berekening zit. Immers is de aanname dat “ware” onderwijsscores relatief stabiel zouden moeten zijn over de tijd heen. Een deel van de verschillen tussen jaren komt door de methode die gebruikt wordt. Bijvoorbeeld door verschillen in geïmputeerde onderwijsscores. In principe is het wenselijk om dat effect te minimaliseren. Om de methodes te vergelijken op hun stabiliteit is een analyse uitgevoerd die ook bij plausibiliteitscontroles van de risico-indicator onderwijsachterstanden wordt uitgevoerd. Hierbij zijn de verschillen in onderwijsscores tussen de jaren 2020 en 2021 op persoonsniveau uitgerekend per imputatiegroep. Dit is gedaan voor zowel de huidige als de nieuwe methode.
Versnippering en herverdeeleffecten. Door de verandering van de methode kan het voorkomen dat scholen die bij de huidige methode niet in aanmerking komen voor aanvullende financiering uit het onderwijsachterstandenbudget bij de nieuwe methode – uitstellen van middeling – wel in aanmerking komen voor extra middelen. Andersom – eerst wel extra middelen, daarna niet – kan ook voorkomen. Tevens kijken we of het aantal scholen dat in aanmerking komt voor extra middelen wijzigt. Dit is gedaan om in kaart te brengen in welke mate het aanpassen van de methode zou leiden tot “versnippering” van het budget. Dat wil zeggen dat veel scholen slechts een klein aandeel van het budget zouden krijgen.
Betrouwbaarheid. Voor het jaar 2021 zijn de varianties en betrouwbaarheidsmarges van de twee methodes met elkaar vergeleken. Bij deze vergelijking werd drie keer de achterstandsscore uitgerekend, waarna de variantie van de score werd bepaald. Deze vergelijking wordt gedaan aan de hand van de parameter K. Kg is een parameter die de bijdrage van een achterstandsleerling in stratum g aan de variantie van de achterstandsscore van de school waarop zij zitten uitdrukt bij twee verschillende (onafhankelijke) berekeningen van achterstandsscores. Kg is een aggregaat van de gemiddelde waarde van de bijdrage en de variantie daaromheen, gewogen naar de kans dat een willekeurige leerling uit stratum g een onderwijsscore heeft die bij minimaal één van de berekeningen onder de grenswaarde van 15% valt. Meer informatie over de berekening en afleiding van Kg is te vinden in Bijlage 2.
Kg is in dit rapport geschat door voor de populatie van 2021 het volledige bijschattingsproces drie keer onafhankelijk uit te voeren. Dit geeft drie mogelijke paarsgewijze vergelijkingen tussen onderwijsscores: (yi1,yi2), (yi1,yi3) en (yi2,yi3) met elk een schatting van Kg. Deze zijn vervolgens gemiddeld. Ook rapporteren we de standaarddeviaties gebaseerd op de spreiding in uitkomsten over deze drie paarsgewijze vergelijkingen. K is vergeleken voor uitgestelde en niet-uitgestelde middeling. Verder zijn in dit onderzoek drie strata onderzocht: drie verschillende subgroepen waarvoor de onderwijsscore wordt geïmputeerd.
2.3 Resultaten
2.3.1 Verschillen in onderwijsscores
De verschillen in individuele onderwijsscores tussen de jaren 2020 en 2021 zijn te zien in figuur 2.3.1 tot 2.3.4. De verwachting was dat het uitstellen van de middeling van onderwijsscores de verschillen tussen onderwijsscores uit opeenvolgende jaren kleiner zou maken. Dit bleek ook het geval: met name voor groepen van wie één of beide ouders onbekend zijn kwamen extreme verschillen (lager dan -2.5 of 2.5 of meer) tussen de jaren minder vaak voor, en minder extreme verschillen juist vaker. Over het geheel genomen namen de verschillen in onderwijsscores van personen tussen opeenvolgende jaren dus af. Dit verschil was het grootste bij kinderen van wie de score was geïmputeerd omdat de vader onbekend is. Bij kinderen die niet staan ingeschreven in de BRP (figuur 2.3.4) zijn wel wat verschuivingen te zien, maar er kan geen duidelijke conclusie getrokken worden dat uitstellen van de middeling een verbetering is.
| Verschil | Huidige methode (Aantal (x1000)) | Nieuwe methode (Aantal (x1000)) |
|---|---|---|
| lager dan -2.5 | 10,248 | 7,691 |
| -2.5 tot -1 | 5,532 | 6,282 |
| -1 tot -0.5 | 2,027 | 2,808 |
| -0.5 tot -0.1 | 1,798 | 2,501 |
| -0.1 tot 0 | 1,49 | 1,448 |
| 0 tot 0.1 | 1,962 | 1,975 |
| 0.1 tot 0.5 | 1,701 | 2,687 |
| 0.5 tot 1 | 2,081 | 3,107 |
| 1 tot 2.5 | 6,044 | 7,095 |
| 2.5 of meer | 11,394 | 8,683 |
| Verschil | Huidige methode (Aantal (x1000)) | Nieuwe methode (Aantal (x1000)) |
|---|---|---|
| lager dan -2.5 | 0,492 | 0,34 |
| -2.5 tot -1 | 0,221 | 0,281 |
| -1 tot -0.5 | 0,084 | 0,125 |
| -0.5 tot -0.1 | 0,066 | 0,118 |
| -0.1 tot 0 | 0,048 | 0,064 |
| 0 tot 0.1 | 0,08 | 0,071 |
| 0.1 tot 0.5 | 0,074 | 0,103 |
| 0.5 tot 1 | 0,108 | 0,135 |
| 1 tot 2.5 | 0,267 | 0,331 |
| 2.5 of meer | 0,547 | 0,419 |
| Verschil | Huidige methode (Aantal (x1000)) | Nieuwe methode (Aantal (x1000)) |
|---|---|---|
| lager dan -2.5 | 10,248 | 7,691 |
| -2.5 tot -1 | 5,532 | 6,282 |
| -1 tot -0.5 | 2,027 | 2,808 |
| -0.5 tot -0.1 | 1,798 | 2,501 |
| -0.1 tot 0 | 1,49 | 1,448 |
| 0 tot 0.1 | 1,962 | 1,975 |
| 0.1 tot 0.5 | 1,701 | 2,687 |
| 0.5 tot 1 | 2,081 | 3,107 |
| 1 tot 2.5 | 6,044 | 7,095 |
| 2.5 of meer | 11,394 | 8,683 |
| Verschil | Huidige methode (Aantal (x1000)) | Nieuwe methode (Aantal (x1000)) |
|---|---|---|
| lager dan -2.5 | 0,327 | 0,336 |
| -2.5 tot -1 | 0,168 | 0,187 |
| -1 tot -0.5 | 0,054 | 0,061 |
| -0.5 tot -0.1 | 0,057 | 0,05 |
| -0.1 tot 0 | 0,036 | 0,026 |
| 0 tot 0.1 | 0,035 | 0,034 |
| 0.1 tot 0.5 | 0,049 | 0,047 |
| 0.5 tot 1 | 0,049 | 0,054 |
| 1 tot 2.5 | 0,182 | 0,17 |
| 2.5 of meer | 0,386 | 0,378 |
2.3.2 Kenmerken van verschillen in achterstandsscores van scholen
In de volgende analyses worden voor verschillende (sub)groepen scholen beschrijvende kenmerken van de jaar-op-jaar verschillen in achterstandsscores getoond. Hierbij is met name de standaarddeviatie een belangrijk kenmerk, omdat deze de mate van spreiding van de jaar-op-jaar verschillen voor de gehele verdeling van een gegeven groep beschrijft. Minima en maxima worden ook getoond, maar deze zijn minder informatief omdat dit slechts de hoogste positieve of negatieve jaar-op-jaar verandering betreft, zonder informatie over de hoeveelheid scholen die in de buurt van die waarde zitten. De minima en maxima betreffen dus vrijwel altijd uitbijters. Wel zouden ze eventueel informatie kunnen verschaffen over of een methode voor een selecte groep scholen beter of slechter werkt. Tenslotte wordt het gemiddelde verschil getoond. Deze gemiddelden moeten rond de 0 zitten en niet teveel verschillen tussen de gebruikte methodes.
In tabel 2.3.5 staan de kenmerken van verschillen in bruto achterstandsscore, dat wil zeggen zonder het toepassen van de drempel, van alle scholen beschreven. In deze tabel staat dus in principe de verdeling van jaar-op-jaar verschillen van achterstandsscores van alle scholen. Wanneer middeling wordt uitgesteld, verandert de verdeling van de jaar-op-jaar verschillen iets ten opzichte van de huidige methode. De grootste verschillen nemen iets toe, te zien in de toename van de onder- en bovengrens, terwijl de algehele spreiding, te zien in de standaarddeviatie, juist afneemt (-2%). Met name dat laatste ligt in de lijn der verwachting: doordat de middeling later in het proces plaatsvindt, wordt het uitrekenen van de achterstandsscore tien keer herhaald, wat in theorie zou moeten leiden tot robuustere uitkomsten en dus minder spreiding (kleinere verschillen) tussen jaren. Het gemiddelde verschil is nagenoeg hetzelfde voor beide methodes.
| Methode | Aantal scholen | Ondergrens | Gemiddelde | Bovengrens | Standaardeviatie |
|---|---|---|---|---|---|
| Huidig | 6 215 | -424,20 | -1,09 | 321,31 | 39,56 |
| Nieuw | 6 215 | -424,78 | -1,21 | 374,93 | 38,79 |
Tabel 2.3.6 beschrijft de kenmerken van verschillen in netto achterstandsscores van scholen, dat wil zeggen met het toepassen van de drempel, die in zowel 2020 als 2021 middelen kregen toebedeeld uit het onderwijsachterstandenbudget. Wanneer middeling wordt uitgesteld, nemen de grootste verschillen wederom toe vergeleken met de huidige methode. Echter neemt zowel het gemiddelde verschil als de standaarddeviatie van het verschil af. Dit betekent dat, hoewel voor enkele scholen de verschillen groter worden wanneer middeling wordt uitgesteld, de algehele spreiding van verschillen in achterstandsscores van scholen die middelen uit het achterstandenbudget krijgen kleiner wordt. De afname van de standaarddeviatie is ook sterker (-5%) dan bij de verschillen in bruto achterstandsscores van alle scholen. Dit kan suggereren dat het uitstellen van de middeling van achterstandsscores een positiever effect heeft voor scholen die in beide jaren middelen krijgen uit het onderwijsachterstandenbudget. Eén van de mogelijke oorzaken hiervan is dat het uitstellen van middeling de imputatie van onderwijsscores robuuster maakt, zoals te lezen in paragraaf 2.3.1. Dat zou betekenen dat scholen waarvan bij relatief veel leerlingen de onderwijsscore is geïmputeerd, meer baat hebben bij het uitstellen van middeling. Om dit te onderzoeken is ook specifiek gekeken naar scholen waarvan een relatief groot deel van de leerlingen geïmputeerd is. Er is voor gekozen om naar scholen te kijken waarvan bij 10% of meer van de leerlingen de onderwijsscore is geïmputeerd, en scholen waarvan bij 25% of meer van de leerlingen de onderwijsscore is geïmputeerd.
| Methode | Aantal scholen | Ondergrens | Gemiddelde | Bovengrens | Standaardeviatie |
|---|---|---|---|---|---|
| Huidig | 2 313 | -330,92 | -2,04 | 284,48 | 49,38 |
| Nieuw | 2 438 | -316,93 | -0,60 | 320,42 | 46,88 |
| Methode | Aantal scholen | Ondergrens | Gemiddelde | Bovengrens | Standaardeviatie |
|---|---|---|---|---|---|
| Huidig | 1 204 | -330,92 | -2,96 | 284,48 | 58,31 |
| Nieuw | 1 204 | -316,93 | 0,22 | 320,42 | 56,84 |
Bij scholen waarvan bij 10% van de leerlingen de onderwijsscore is geïmputeerd, neemt de standaarddeviatie, net als bij de gehele populatie scholen, af (-2,5%) wanneer middeling wordt uitgesteld ten opzichte van de huidige methode. Deze afname is wel minder sterk dan bij alle scholen die in beide jaren middelen krijgen uit het onderwijsachterstandenbudget. Het gemiddelde verschil neemt ook een beetje af, net als het maximale negatieve verschil. Het maximale positieve verschil wordt juist groter. Om te onderzoeken in welke mate deze verschillen te maken hebben met jaar-op-jaar verschillen in het aantal imputaties op een school, is ook gekeken naar scholen met 10% of meer leerlingen met geïmputeerde onderwijsscores, waarvan het jaar-op-jaar verschil in percentage leerlingen met geïmputeerde onderwijsscores niet hoger was dan ± 5% (tabel 2.3.8).
| Methode | Aantal scholen | Ondergrens | Gemiddelde | Bovengrens | Standaardeviatie |
|---|---|---|---|---|---|
| Huidig | 1 107 | -216,07 | -5,28 | 216,16 | 53,27 |
| Nieuw | 1 107 | -291,58 | -2,72 | 214,24 | 50,76 |
Bij scholen waarvan bij minimaal 10% van de leerlingen de onderwijsscore is geïmputeerd was en waarbij er geen grote jaar-op-jaar verschillen waren in het percentage imputaties, nemen zowel het gemiddelde verschil als de standaard deviatie (-5%) af wanneer middeling wordt uitgesteld ten opzichte van de huidige methode. Het maximale negatieve verschil neemt juist toe. Ook hier kan geconcludeerd worden dat individuele scholen misschien grotere verschillen vertonen jaar op jaar, maar de algehele spreiding van verschillen voor alle scholen in deze subset verkleint.
| Methode | Aantal scholen | Ondergrens | Gemiddelde | Bovengrens | Standaardeviatie |
|---|---|---|---|---|---|
| Huidig | 239 | -216,07 | -0,28 | 284,48 | 80,02 |
| Nieuw | 239 | -212,53 | 5,48 | 320,42 | 79,30 |
Bij scholen waarvan bij minimaal 25% van de leerlingen de onderwijsscore is geïmputeerd, neemt de standaarddeviatie wederom af; zie tabel 2.3.9. Deze afname is wel relatief klein. Net als in voorgaande vergelijkingen neemt het maximale positieve verschil toe. Anders dan bij andere vergelijkingen neemt het gemiddelde verschil iets toe wanneer middeling wordt uitgesteld. Dat verschil is echter niet groot. Ook voor deze subgroep is verder gekeken naar scholen die kleine jaar-op-jaar verschillen hadden in het aantal imputaties, te zien in tabel 2.3.10.
| Methode | Aantal scholen | Ondergrens | Gemiddelde | Bovengrens | Standaardeviatie |
|---|---|---|---|---|---|
| Huidig | 196 | -216,07 | -10,11 | 216,16 | 70,13 |
| Nieuw | 196 | -212,53 | -6,83 | 208,34 | 67,37 |
Bij deze scholen neemt de standaarddeviatie af wanneer middeling wordt uitgesteld. Dit effect is iets sterker dan in de gehele groep scholen met meer dan 25% imputaties. Anders dan in tabel 2.3.8 is te zien, nemen ook het gemiddelde verschil en het maximale positieve verschil iets af ten opzichte van de huidige methode.
2.3.3 Kenmerken van jaar-op-jaar verschillen in bruto en netto achterstandsscores op gemeenteniveau
Tabel 2.3.11 toont jaar-op-jaar verschillen in bruto achterstandsscores voor gemeentes, uitgesplitst naar methode. Hieruit is op te maken dat wanneer middeling wordt uitgesteld, alle kenmerken lager uitvallen ten opzichte van de huidige methode. In het bijzonder neemt de standaarddeviatie af met 27%. Dat is een aanzienlijk verschil, en veel groter dan de verschillen die te zien waren op schoolniveau.
| Methode | Aantal gemeenten | Ondergrens | Gemiddelde | Bovengrens | Standaardeviatie |
|---|---|---|---|---|---|
| Huidig | 352 | -4204,36 | -33,46 | 653,53 | 318,6 |
| Nieuw | 352 | -3291,34 | -31,25 | 326,86 | 232,17 |
Tabel 2.3.12 toont jaar-op-jaar verschillen in netto achterstandsscores voor alle gemeentes, uitgesplitst naar methode. Net als bij de bruto achterstandsscores nemen alle kenmerken af wanneer middeling wordt uitgesteld ten opzichte van de huidige methode. In het bijzonder neemt de standaarddeviatie af met 31%.
| Methode | Aantal gemeenten | Ondergrens | Gemiddelde | Bovengrens | Standaardeviatie |
|---|---|---|---|---|---|
| Huidig | 352 | -3 702,31 | -23,06 | 662,43 | 286,73 |
| Nieuw | 352 | -2772,3 | -20,70 | 317,46 | 198,44 |
2.3.4 Verschillen in verdeling van het onderwijsachterstandenbudget wanneer middeling zou worden uitgesteld.
In tabel 2.3.13 wordt per jaar getoond hoeveel extra scholen middelen zouden krijgen wanneer middeling zou worden uitgesteld ten opzichte van de huidige methode. Dat aantal varieert van 159 (2021) tot 281 (2019). Daarnaast is te zien hoeveel procent van het onderwijsachterstandenbudget naar deze scholen zou gaan per jaar. Dit varieert van 0,410% (2021) tot 0,728% (2019). Dit zijn relatief lage percentages, waardoor geconcludeerd kan worden dat het uitstellen van middeling van achterstandsscores niet leidt tot versnippering van het budget.
| 2019 | 2020 | 2021 | |
|---|---|---|---|
| Aantal | 281 | 200 | 159 |
| % budget | 0,728% | 0,465% | 0,410% |
Tenslotte is ook onderzocht hoeveel scholen volgens de huidige methode wel middelen krijgen uit het onderwijsachterstandenbudget, maar wanneer middeling wordt uitgesteld niet meer. In 2019 zouden dit 49 scholen zijn; in 2020 62 scholen, en in 2021 67 scholen. Er zijn dus maar weinig scholen die volgens de huidige methode wel middelen toebedeeld krijgen en dat niet meer zouden krijgen wanneer middeling wordt uitgesteld.
2.3.5 Vergelijking van parameter K met en zonder uitstellen van middeling
Zoals genoemd in de methodesectie is de parameter K uitgerekend voor achterstandsscores waarbij middeling is uitgesteld en scores waarbij dat niet het geval was. In tabel 2.3.14 zijn de parameterwaarden te zien voor de verschillende strata. Zoals genoemd zijn hier alleen de strata geanalyseerd waarin de opleidingsniveaus van de moeder, de vader of beide ouders onbekend zijn, omdat het uitstellen van de middeling in principe alleen op deze leerlingen effect heeft. Daarnaast zijn dit ook de strata die het meeste invloed hebben op de variantie van de achterstandsscores (en de hoogste K waarde hebben). In principe is een lage waarde voor K wenselijk, omdat dit een lagere variantie in achterstandsscores tot gevolg heeft.
| Stratum | K (uitgestelde middeling) | K (zonder uitgestelde middeling) |
|---|---|---|
| Beide onbekend | 0,882 | 7,866 |
| Vader onbekend | 0,552 | 4,399 |
| Moeder onbekend | 0,563 | 4,549 |
| Beide onbekend (sd) | 0,035 | 0,048 |
| Vader onbekend (sd) | 0,007 | 0,060 |
| Moeder onbekend (sd) | 0,033 | 0,235 |
Zowel de waarde van K als de standaarddeviatie van K zijn aanzienlijk lager voor alle strata wanneer middeling wordt uitgesteld dan wanneer dit niet wordt gedaan. Dit betekent dat wanneer de middeling van achterstandsscores wordt uitgesteld, leerlingen van wie het opleidingsniveau van minimaal één ouder wordt geïmputeerd aanzienlijk minder bijdragen aan de variantie in achterstandsscore van de school waarop zij zitten. Dit leidt vervolgens tot significant minder variantie in achterstandsscores van scholen of gemeentes in het algemeen, maar in het bijzonder van die scholen of gemeentes waarin veel leerlingen aanwezig zijn van wie één of beide ouders onbekend zijn.
2.4 Conclusies
In dit onderzoek werd onderzocht welke effecten het uitstellen van middeling bij het berekenen van achterstandsscores heeft. Hier is gekeken naar de verdeling van jaar-op-jaar verschillen van individuele onderwijsscores, de verdeling van financiering op basis van achterstandsscores, de verdeling van jaar-op-jaar verschillen in achterstandsscores op school- en gemeenteniveau, en de variantiebijdrage aan achterstandsscores van leerlingen van wie het opleidingsniveau van één of beide ouders geïmputeerd is.
Uit de resultaten van het onderzoek blijkt dat het uitstellen van middeling van achterstandsscores leidt tot kleinere verschillen in individuele onderwijsscores tussen verschillende jaren, met name voor leerlingen van wie het opleidingsniveau van één of beide ouders onbekend is. Bij kinderen die niet bekend zijn in de BRP is dit nauwelijks het geval. Ook is de spreiding van jaar-op-jaar verschillen in zowel bruto (zonder drempel) als netto (met drempel) achterstandsscores lager wanneer middeling wordt uitgesteld. Deze vermindering is bescheiden, maar is wel groter wanneer wordt gekeken naar scholen die in beide jaren relatief veel geïmputeerde leerlingen hadden. Daarentegen neemt de spreiding van jaar-op-jaar verschillen in achterstandsscores op gemeenteniveau wel fors af wanneer middeling wordt uitgesteld.
Daarnaast leidt uitstelling van middeling tot een lagere variantiebijdrage van leerlingen van wie het opleidingsniveau van één of beide ouders geïmputeerd was doordat voor deze groepen zowel de waarde als de standaarddeviatie van parameter K lager is wanneer middeling wordt uitgesteld. Het effect hiervan is groot: het uitstellen van middeling verlaagde de grootte van K met 85-90%. Het gevolg hiervan is dat de standaardfout van achterstandsscores kleiner wordt, wat leidt tot minder variantie in achterstandsscores voor scholen met veel leerlingen die behoren tot de genoemde groepen. Dat is een positief resultaat omdat de ervaring leert dat juist scholen met relatief veel geïmputeerde leerlingen veel fluctueren in hun achterstandsscores over verschillende jaren ten gevolge van fluctuaties in geïmputeerde scores. Dat betekent dat deze scholen deels verschillen in achterstandsscores door de gebruikte methode en niet door veranderingen in variabelen onderliggend aan achterstandsscores. Het verminderen van deze variantie leidt dus tot consistentere achterstandsscores over meerdere jaren, wat ook beter aansluit bij de “echte” situatie. Dat wil zeggen, veranderingen komen in mindere mate door onzekerheid bij het imputeren van ontbrekende informatie en dus relatief in meerdere mate door veranderingen in de daadwerkelijke situatie van een school. Dit is dan ook een mogelijke verklaring voor het feit dat uitstellen van middeling leidt tot minder spreiding van jaar-op-jaar verschillen in achterstandsscores op zowel school- als gemeenteniveau.
Tenslotte is onderzocht welke effecten het uitstellen van middeling zou hebben op de daadwerkelijke verdeling van het onderwijsachterstandenbudget. Met name of dit zou leiden tot “versnippering” van het budget, waarbij veel scholen relatief weinig budget zouden ontvangen met als gevolg dat deze scholen slechts beperkt effectieve maatregelen zouden kunnen nemen om onderwijsachterstanden te bestrijden. Een ander mogelijk gevolg dat werd onderzocht was of verandering in methodiek zou leiden tot een grote verschuiving in welke scholen middelen uit het onderwijsachterstandenbudget toebedeeld zouden krijgen. In dit onderzoek is geen indicatie gevonden dat deze zaken in belangrijke mate zouden plaatsvinden wanneer besloten wordt om middeling van achterstandsscores uit te stellen.
Kortom, Het uitstellen van het middelen van achterstandsscores lijkt positieve gevolgen te hebben voor de robuustheid van individuele onderwijsscores, en achterstandsscores op school- en gemeenteniveau. Daarnaast lijken geanticipeerde nadelen niet, of in zeer beperkte mate, aanwezig.
3. Imputatie ontbrekende opleidingsniveaus
3.1 Inleiding
Het opleidingsniveau van de ouders is een belangrijke voorspeller met betrekking tot het risico op onderwijsachterstand van een kind (CBS, 2019). Voor ouders die zijn ingeschreven in de Basisregistratie Persoonsgegevens is dit kenmerk beschikbaar uit het Opleidingsniveaubestand van het CBS. De opleidingsniveaus in dit bestand zijn deels afgeleid uit centrale opleidingsregisters en deels uit steekproefdata van de Enquête Beroepsbevolking (EBB).
Voor een aanzienlijk deel van de ouders in de BRP is geen opleidingsniveau bekend in het Opleidingsniveaubestand (Linder et al., 2011). Deels komt dit doordat centrale opleidingsregisters nog niet lang worden bijgehouden: voor het hoger onderwijs sinds het midden van de jaren 1980, voor het voortgezet onderwijs en mbo rond de eeuwwisseling en voor het primair onderwijs vanaf 2010. Mensen die hun opleiding al hadden afgerond voordat de relevante registers beschikbaar kwamen zijn daarom alleen op steekproefbasis waargenomen in de EBB. Verder ontbreekt in de registers alle informatie over opleidingen die mensen in het buitenland hebben gevolgd. Van oudere mensen en mensen die op latere leeftijd naar Nederland zijn gekomen is daarom relatief vaak geen opleidingsniveau bekend. Omdat de EBB-data elk jaar worden aangevuld met een nieuwe steekproef, neemt het percentage ontbrekende opleidingsniveaus in het bestand in de loop van de tijd af.
In het Opleidingsniveaubestand heeft elke persoon met een bekend opleidingsniveau een ophooggewicht. Dit gewicht is gelijk aan 1 als de informatie uit een register komt en ongelijk aan 1 als de informatie (alleen) uit de EBB komt. Met deze ophooggewichten kan een goede schatting worden gemaakt van de verdeling van opleidingsniveau voor de hele Nederlandse bevolking.
Binnen de groep kinderen van wie beide ouders voorkomen in de BRP onderscheiden we vier deelpopulaties:
- het opleidingsniveau van zowel de moeder als de vader is onbekend;
- het opleidingsniveau van de moeder is bekend, het opleidingsniveau van de vader niet;
- het opleidingsniveau van de vader is bekend, het opleidingsniveau van de moeder niet;
- het opleidingsniveau van zowel de moeder als de vader is bekend.
| deelpopulatie | kinderen t/m 27 jaar | kinderen t/m 12 jaar |
|---|---|---|
| A | 15,50% | 7,90% |
| B | 17,20% | 13,20% |
| C | 11,70% | 7,80% |
| D | 55,60% | 71,10% |
Tabel 3.1.1 geeft een indruk van de omvang van het probleem met ontbrekende waarden: hoe ouder de kinderen, hoe meer ouders er voorkomen met een onbekend opleidingsniveau. Van alle kinderen in de BRP tot en met 27 jaar heeft ongeveer 44% ten minste één ouder met een onbekend opleidingsniveau. In ruim 15% van de gevallen zijn beide opleidingsniveaus onbekend. Bij kinderen tot en met 12 jaar (primair onderwijs en jonger) komen minder ontbrekende waarden voor, doordat de ouders gemiddeld jonger zijn. Binnen deze groep heeft ongeveer 29% ten minste één ouder met een onbekend opleidingsniveau, terwijl voor slechts 8% het opleidingsniveau van beide ouders tegelijk onbekend is. Verder is te zien dat het opleidingsniveau van de vader relatief vaker ontbreekt dan het opleidingsniveau van de moeder.
Om toch het risico op onderwijsachterstand in te kunnen schatten, worden de onbekende opleidingsniveaus alsnog geschat en geïmputeerd met specifieke statistische methoden. Bij het imputeren wordt gebruikgemaakt van andere kenmerken die wel bekend zijn uit registraties en die samenhangen met het opleidingsniveau van een persoon, zoals het inkomen en (indien bekend) het opleidingsniveau van de partner. Op basis van dergelijke kenmerken wordt een schatting gemaakt van de onbekende opleidingsniveaus. Omdat deze schattingsmodellen een bepaalde mate aan variatie kennen, kunnen meerdere schattingen voor één persoon tot verschillende uitkomsten leiden. Op individueel niveau zal deze schatting daardoor niet altijd kloppen, maar gemiddeld over grotere groepen mensen geven de uitkomsten een betrouwbare schatting van de werkelijke verdeling van het opleidingsniveau. Het verbeteren van de schattingsmethode kan leiden tot een kleinere variatie in uitkomsten en dientengevolge een stabielere schatting over de tijd.
De plausibiliteitsanalyses die het CBS jaarlijks met betrekking tot de achterstandsscores publiceert, laten een aantal zaken hieromtrent zien. Op populatieniveau laten de jaar-op-jaar vergelijkingen zien dat de uitkomsten vergelijkbaar zijn met voorgaande jaren met een licht opwaartse trend van het opleidingsniveau. Tevens laten deze jaar-op-jaar vergelijkingen zien dat de onderwijsscores van jaar op jaar aanzienlijk sterker fluctueren bij kinderen van wie bij één of beide ouders het opleidingsniveaus is geïmputeerd in vergelijking tot kinderen van wie van beide ouders het opleidingsniveau bekend is5).
Hoewel deze fluctuaties zich op populatieniveau uitmiddelen, hoeft dit niet het geval te zijn bij kleinere subpopulaties. De leerlingenpopulatie van een school is zo’n kleinere subpopulatie. Het gevolg is dat de achterstandsscore van een school waar relatief veel opleidingsniveaus worden geïmputeerd instabieler is. Verbetering van de methoden voor het imputeren van ontbrekende opleidingsniveaus van de ouders van kinderen kan leiden tot een stabielere achterstandsscore en dus een betere voorspelbaarheid van het toegekende budget door OCW. Verbetering van de imputatiemethodiek kan worden gezocht in het verbeteren van de variabelen die nu al worden gebruikt (inkomen, opleidingsniveau partner, herkomst, burgerlijke staat, inkomstenbron en mate van stedelijkheid), in het toevoegen van nieuwe variabelen en het gebruik van een andere statistische methode voor het schatten en imputeren van ontbrekende opleidingsniveaus. De huidige methodiek voor de risico-indicator maakt gebruik van ‘continuation-ratio logistische regressie’. Multinomiale logistische regressie is daarbij een logisch alternatief om te onderzoeken.
Ook de kenmerken die gebruikt worden bij het schatten van ontbrekende opleidingsniveaus bevatten soms voor een klein deel ontbrekende waarden. Deze kenmerken worden nu compleet gemaakt middels een mice-methodiek (multiple imputations with chained equations). Afhankelijk van het type variabele wordt voor een bepaalde standaardmethode gekozen. Voor numerieke data is dat predictive mean matching, logistische regressie voor binaire data en multinomiale regressie en proportional odds regressie voor respectievelijk ongeordende en geordende categorische data met meer dan twee categorieën. Door de omvang van de populatie is deze manier van imputeren zeer rekenintensief.
Dit deelonderzoek bestaat daarom zelf ook weer uit een drietal onderdelen: verbetering van de imputatie van ontbrekende waarden bij hulpvariabelen; een vergelijking van alternatieve regressiemethodieken voor de imputatie van ontbrekende opleidingsniveaus en een onderzoek naar de verbetering van de imputatie van ontbrekende opleidingsniveaus met behulp van meer en/of betere achtergrondkenmerken.
3.2 Data en methoden
3.2.1 Imputatie hulpvariabelen
Voor de imputatie van hulpvariabelen wordt er geïmputeerd met het mice-package (van Buuren en Groothuis-Oudshoorn, 2011) in R, waarbij gebruikt wordt gemaakt van multipele imputatie. In de huidige toepassing voor de risico-indicator onderwijsachterstanden worden met mice de standaard methoden gebruikt, die afhankelijk zijn van het type kenmerk dat wordt geïmputeerd. Bij een numeriek kenmerk, zoals het inkomen, wordt er gebruik gemaakt van predictive mean matching. Bij de andere categorische kenmerken wordt er gebruik gemaakt van polytome (multinomiale) regressie. Bij de methode predictive mean matching voor numerieke kenmerken wordt er voor elke persoon met ontbrekende waarden, een ‘donor’ gezocht die geen ontbrekende waarden heeft. Deze donor wordt gevonden door een regressiemodel toe te passen op de groep zonder ontbrekende waarden, met behulp van een set achtergrondkenmerken. Het regressiemodel berekent een voorspelde waarde per persoon, door de samenhang te bekijken tussen de achtergrondkenmerken en het te imputeren kenmerk. Vervolgens wordt er een donor gevonden door de persoon te koppelen aan iemand met een vergelijkbare voorspelde waarde door het regressiemodel. De methode voor categorische variabelen, polytome (multinomiale) regressie, is een verlenging van een logistisch regressiemodel, waarbij de kans op een categorie voor meer dan twee uitkomsten geschat wordt. Per categorie wordt er een logistisch regressiemodel geschat, voor de categorie in vergelijking met een referentiegroep.
Het gebruik van de verschillende standaardmethoden in mice kost veel rekentijd. Doordat er tien iteraties worden uitgevoerd én we dit toepassen op een grote dataset is de rekenintensiteit erg hoog. Bij predictive mean matching kan de rekentijd oplopen doordat het tijd kost een donor te vinden voor elke persoon met ontbrekende waarden. Daarnaast kost polytome regressie veel tijd omdat voor iedere categorie een apart logistisch regressiemodel geschat moet worden.
Daarom onderzoeken we of we de imputatie sneller kunnen maken zonder in te boeten op de kwaliteit van de imputatie. Daarnaast onderzoeken we welke imputatietechniek beter aansluit bij het gebruik van zowel continue als categorische achtergrondkenmerken. Om de imputatie van het opleidingsniveau te verbeteren, is het ook van belang om de imputatie van de andere ontbrekende registerkenmerken te verbeteren. We onderzoeken daarom ook of het imputatiemodel verbeterd kan worden door aanvullende achtergrondkenmerken te gebruiken.
Omdat de methode predictive mean matching vooral geschikt is voor continue variabelen, testen we methoden die kunnen omgaan met zowel categorische als continue variabelen. We testen hiervoor andere technieken voor donorimputatie en technieken gebaseerd op beslisbomen.
Voor de donorimputatie testen we twee technieken: 1) K-Nearest Neighbours (KNN) en 2) Hotdeck imputatie. Bij KNN wordt er een afstand berekend op basis van een set achtergrondkenmerken, met een gekozen afstandsfunctie. Vervolgens wordt de afstand berekend tussen de donoren en ontvangers, waarna een donor wordt geselecteerd uit de K dichtstbijzijnde donoren. Bij de hotdeck imputatie worden er homogene groepjes gevormd op basis van de achtergrondkenmerken, waarna een willekeurige donor wordt geselecteerd binnen het groepje. Deze technieken kunnen goed toegepast worden als er meerdere kenmerken tegelijk ontbreken. Daarnaast kunnen ze omgaan met categorische variabelen.
Daarnaast is er gekeken naar technieken die gebruikmaken van beslisbomen: 1) Classification and Regression Trees (CART) en 2) Random forest. Beide technieken zijn machine learning algoritmen voor het maken van beslisbomen. In een beslisboom wordt de data opgedeeld in subgroepen op basis van de achtergrondkenmerken die het meest onderscheidend zijn. CART kan gebruikt worden voor continue en categoriale variabelen. Een random forest gaat hierin nog verder door niet één, maar meerdere beslisbomen te schatten. Bij imputatie zal de beslisboom eerst op de groep geschat worden zonder ontbrekende waarden, waarna voor de groep met ontbrekende waarden een voorspelde waarde of categorie berekend kan worden voor de ontbrekende waarde. De imputatietechnieken zijn beoordeeld op een tweetal aspecten: stabiliteit en snelheid.
3.2.2 Regressiemethodiek opleidingsniveau
Binnen de risico-indicator onderwijsachterstanden wordt gewerkt met een indeling van opleidingsniveau in acht categorieën. Het idee achter de imputatiemethode is dat voor elke ouder in het bestand eerst een kansverdeling over de acht categorieën wordt geschat: (p1i,…,p8i), waarbij pci de kans is dat persoon i opleidingsniveau c heeft (c∈{1,…,8}). Vervolgens wordt met deze kansen een trekking gedaan om één van de categorieën te imputeren bij persoon i. Om stabielere resultaten te vinden wordt deze procedure J=10 keer herhaald, zodat uiteindelijk bij elke persoon met een onbekend opleidingsniveau tien waarden worden geïmputeerd.
In de imputatiemethode worden de kansen pci gemodelleerd via een variant op logistische regressie. Het bekende binaire logistische regressiemodel is bedoeld voor kenmerken met twee categorieën en kan daarom hier niet direct worden toegepast. De meest eenvoudige uitbreiding naar meer dan twee categorieën is multinomiale logistische regressie. Hierbij wordt een model van de volgende vorm gebruikt (Agresti, 2013):
$$\log\left( \frac{p_{ci}}{p_{8i}} \right) = \beta_{c0} + \beta_{c1}x_{1i} + \ldots + \beta_{cL}x_{Li},\ \ \ \ \ (c = 1,\ldots,7).$$
De laatste (achtste) categorie van opleidingsniveau is hierbij de referentiecategorie. De variabelen x1i,…,xLi zijn achtergrondkenmerken in het imputatiemodel.
Voor het imputeren van opleidingsniveau binnen de huidige indicator wordt een andere variant op logistische regressie gebruikt: continuation-ratio logistische regressie. Zie Agresti (2013) of CBS (2016) voor een beschrijving van dit model. Het belangrijkste verschil met multinomiale logistische regressie is dat continuation-ratio regressie expliciet rekening houdt met het feit dat opleidingsniveau een ordinale variabele is, met een ordening in de categorieën van laag naar hoog. In theorie zou dit tot betere imputaties kunnen leiden, al verdwijnt dit voordeel als de steekproef waarop het model geschat wordt voldoende groot is. Daar staat tegenover dat multinomiale logistische regressie twee voordelen heeft ten opzichte van continuation-ratio logistische regressie:
- De imputatiemethode is eenvoudiger te implementeren omdat standaard-software beschikbaar is voor het schatten van dit model (zoals het R-pakket nnet). Dit maakt de code eenvoudiger te onderhouden dan bij continuation-ratio logistische regressie, waarvoor een eigen implementatie moest worden geschreven.
- In een eerdere toepassing bij de Volkstelling bleek dat multinomiale logistische regressie leidde tot stabielere uitkomsten dan continuation-ratio logistische regressie (Daalmans, 2021).
We hebben daarom onderzocht of multinomiale logistische regressie een geschikt alternatief is voor het imputeren van opleidingsniveau bij de onderwijsachterstandsindicator. Voor de analyse voor dit onderdeel is de dataset gebruikt waarmee ook de risico-indicator onderwijsachterstanden voor peildatum 1 februari 2022 is berekend.
3.2.3 Imputatie opleidingsniveau
Voor de huidige indicator voor onderwijsachterstanden is een methode ontwikkeld om de ontbrekende opleidingsniveaus te imputeren (CBS, 2016). Deze methode bestaat uit drie stappen:
- Imputeer de ontbrekende opleidingsniveaus bij moeders in deelpopulatie C, gebruikmakend van de beschikbare informatie uit deelpopulatie D.
- Imputeer de ontbrekende opleidingsniveaus bij vaders in deelpopulatie B, gebruikmakend van de beschikbare informatie uit deelpopulatie C en D.
- Imputeer de ontbrekende opleidingsniveaus bij moeders en vaders in deelpopulatie A, gebruikmakend van de beschikbare informatie uit deelpopulatie B, C en D.
Er blijkt een relatief sterke samenhang te bestaan tussen de opleidingsniveaus van beide ouders van hetzelfde kind. In stap 1 en 2 wordt daarom gebruikgemaakt van het bekende opleidingsniveau van de ene ouder bij het imputeren van het onbekende opleidingsniveau van de andere ouder. In stap 3, bij de deelpopulatie waar beide opleidingsniveaus onbekend zijn, wordt eerst het opleidingsniveau van de moeder geïmputeerd. Vervolgens wordt het opleidingsniveau van de vader geïmputeerd, waarbij rekening wordt gehouden met het geïmputeerde opleidingsniveau van de moeder, zodat de samenhang tussen de twee kenmerken behouden blijft.
De bestaande imputatiemethode maakt gebruik van de volgende modellen voor de drie deelpopulaties C, B en A (een getal tussen haken geeft aan in hoeveel categorieën het betreffende kenmerk is ingedeeld.):
- Deelpopulatie C (moeders):
opleidingsniveau vader [8] × (inkomen moeder [4] + herkomstgroepering moeder [8] + leeftijd moeder [5] + stedelijkheidsgraad buurt [6] + burgerlijke staat moeder [3] + sociaaleconomische categorie moeder [2]) - Deelpopulatie B (vaders):
opleidingsniveau moeder [8] × (inkomen vader [4] + herkomstgroepering vader [8] + leeftijd vader [5] + stedelijkheidsgraad buurt [6] + burgerlijke staat vader [3] + sociaaleconomische categorie vader [2]) - Deelpopulatie A (moeders):
inkomen moeder [4] × (herkomstgroepering moeder [8] + leeftijd moeder [5] + stedelijkheidsgraad buurt [6] + burgerlijke staat moeder [3] + sociaaleconomische categorie moeder [2]) - Deelpopulatie A (vaders):
hetzelfde model als bij deelpopulatie B
Doel van dit onderzoek is om te bepalen of deze modellen kunnen worden verbeterd door andere kenmerken te kiezen en/of andere indelingen van de bestaande kenmerken te gebruiken. De volgende aanpak is gevolgd, waarbij gebruik is gemaakt van een populatiebestand over 2021:
- Op inhoudelijke gronden is een voorselectie gemaakt van kenmerken die mogelijk interessant zijn voor het imputeren van opleidingsniveau. Bij sommige kenmerken zijn verschillende mogelijke indelingen voorgesteld. Op basis van een stapsgewijze regressieanalyse is per kenmerk één indeling geselecteerd en zijn de geselecteerde kenmerken gerangschikt in aflopende volgorde van hun voorspelkracht voor opleidingsniveau.
- Verschillende modellen die gebruikmaken van de geselecteerde kenmerken uit de stapsgewijze regressieanalyse zijn vergeleken in een simulatiestudie. Hierbij zijn extra ontbrekende waarden aangebracht bij ouders met bekende opleidingsniveaus, zodat de kwaliteit van de imputaties kan worden geëvalueerd.
- Voor een extra validatie is gezocht naar ouders met een onbekend opleidingsniveau in het bestand van 2021 maar een bekend opleidingsniveau in het bestand van 2022. Voor deze ouders zijn de imputaties uit de modellen voor 2021 vergeleken met de waargenomen opleidingsniveaus uit 2022, onder de aanname dat het opleidingsniveau in de tussentijd niet is veranderd.
Kenmerken zijn interessant als hulpvariabele voor het imputeren van opleidingsniveau als ze (sterk) samenhangen met opleidingsniveau en/of een grote kans hebben om opgenomen te worden in het uiteindelijke analysemodel voor onderwijsachterstanden. Kenmerken die aan beide criteria tegelijk voldoen zijn daarbij het meest interessant.
Op basis van bovenstaande overweging en beschikbaarheid van data in het Stelsel van Sociaal-statistische Bestanden (SSB) bij het CBS is de volgende longlist gemaakt van kenmerken om te onderzoeken:
- opleidingsniveau andere ouder [8*]
- leeftijd ouder [5*, 8 of in jaren]
- burgerlijke staat ouder [3* of 4]
- herkomstgroepering ouder [8*]
- inkomen ouder [4*, 5, 6, 11, 21 of continu]
- welvaart huishouden [5, 6, 11 of 21]
- sociaaleconomische categorie ouder [2* of 13]
- type economische activiteit werkgever ouder [12]
- deeltijdfactor werk ouder [5, 6 of 11]
- stedelijkheidsgraad buurt [6*]
- leeftijd kind [in jaren]
Een getal tussen haken geeft aan in hoeveel categorieën het betreffende kenmerk is ingedeeld. Een asterisk * geeft aan dat de betreffende indeling is gebruikt in het huidige imputatiemodel.
Selectie van kenmerken
Vervolgens selecteren we met een combinatie van bivariate analyses en een stepwise-procedure de kenmerken die een bijdrage leveren aan het schatten van ontbrekende opleidingsniveaus. Voor moeder en vader apart wordt de bivariate relatie tussen opleidingsniveau en elk kenmerk apart geanalyseerd door een multinomiale logistische regressie te schatten voor opleidingsniveau met één kenmerk tegelijk als voorspeller, voor ouders met bekende opleidingsniveaus. Als evaluatiematen kijken we per model naar de AIC (Agresti, 2013) en naar de verwachte fractie imputaties die exact gelijk zijn aan de juiste categorie (κ0) of daar maximaal één categorie naast zitten (κ1):
$$\begin{align} E\left(\kappa_{0} \right) &= \sum_{l = 1}^{L}\frac{N_{l}}{N}\sum_{c = 1}^{8}p_{lc}^{2},\\ E\left( \kappa_{1} \right) &= E\left( \kappa_{0} \right) + 2\sum_{l = 1}^{L}\frac{N_{l}}{N}\sum_{c = 1}^{7}{p_{lc}}p_{l(c + 1)}. \end{align}$$
Hierbij is L het aantal categorieën van de hulpvariabele; N is het totaal aantal records in de dataset; Nl het aantal records met categorie l op de hulpvariabele; ten slotte is plc de fractie records met categorie l op de hulpvariabele en opleidingsniveau c, als fractie van Nl. Voor een afleiding van de formules voor E(κ0) en E(κ1), zie Scholtus en Pannekoek (2015). Een model past beter bij de data als de AIC lager is en leidt naar verwachting tot betere imputaties als E(κ0) en E(κ1) hoger zijn.
Simulatiestudie
Na de selectie van de kenmerken kunnen we met een simulatie een schatting maken van de mate waarin de modellen met de geselecteerde kenmerken ontbrekende opleidingsniveaus correct voorspellen. De opzet van de simulatiestudie is als volgt:
a. Binnen de groep kinderen voor wie het opleidingsniveau van beide ouders bekend is
verwijderen we steeds willekeurig voor (ongeveer) 5% van de ouders de
waargenomen opleidingsniveaus. (De manier waarop dit gebeurt luistert vrij nauw,
omdat de extra ontbrekende waarden min of meer dezelfde verdeling moeten hebben
als de waarden die in het oorspronkelijke bestand al ontbreken, anders werkt de
imputatiemethode voor deze extra ontbrekende waarden niet goed. Zie de toelichting
hieronder). We herhalen dit voor S=5 simulatieronden.
b. Per simulatieronde voeren we J=10 imputaties uit van alle ouders met onbekende
opleidingsniveaus (inclusief de zojuist verwijderde waarden) met elk van de
geselecteerde modellen. Ter vergelijking passen we daarnaast ook het imputatiemodel
uit de huidige indicator toe (maar wel gebruikmakend van multinomiale logistische
regressie).
c. Per simulatieronde en model berekenen we onderwijsscores [volgens de huidige
regeling zoals beschreven in CBS (2019)] op basis van de tien imputaties voor de
kinderen met ouders met verwijderde opleidingsniveaus en vergelijken deze met de
onderwijsscores die zouden zijn berekend als de opleidingsniveaus niet waren
verwijderd.
Toelichting bij stap (a): om bij het simuleren van nieuwe ontbrekende waarden aan te sluiten bij de werkelijke verdeling van ontbrekende waarden in het Opleidingsniveaubestand wordt de volgende aanpak gevolgd. Bij de moeders worden extra ontbrekende waarden gesimuleerd binnen de personen voor wie het opleidingsniveau (ook) in de EBB is waargenomen, waarbij de kans om te ontbreken per record evenredig is met het gewicht van de moeder uit het Opleidingsniveaubestand. Het achterliggende idee is dat een record met gewicht = w in feite w moeders in de echte populatie representeert, die allemaal hadden kunnen ontbreken. De ontbrekende waarden worden gesimuleerd door eerst een pseudopopulatie te genereren met van elk beschikbaar record w kopieën (afgerond op het dichtstbijzijnde gehele getal) en daaruit een enkelvoudig aselecte steekproef van 5% te trekken. Van alle moeders van wie minimaal één kopie is getrokken in de steekproef wordt het opleidingsniveau ontbrekend gemaakt. Bij de vaders werkt dit analoog. Gemakshalve worden de ontbrekende waarden bij moeders en vaders onafhankelijk van elkaar gesimuleerd.
NB: bij de ontwikkeling van het imputatiemodel voor de oorspronkelijke indicator is een soortgelijke aanpak gevolgd (CBS, 2016), alleen kon daar gebruik worden gemaakt van data uit het COOL-onderzoek, waarin het opleidingsniveau van beide ouders altijd was waargenomen (zij het volgens een andere indeling dan in het Opleidingsniveaubestand). Een simulatiestudie kon daarom worden gedaan door ontbrekende waarden aan te brengen in de COOL-data voor precies die ouders van wie het opleidingsniveau ontbrak in het Opleidingsniveaubestand. Dit leidde vanzelf tot een realistisch patroon van ontbrekende waarden.
We berekenen de volgende evaluatiematen:
- Per simulatieronde en model berekenen we de gemiddelde geïmputeerde verdeling van opleidingsniveau bij de ouders met verwijderde opleidingsniveaus en vergelijken deze met de werkelijke verdeling voor deze ouders. Per model berekenen we het gemiddelde en de standaarddeviatie van de afwijking tussen de twee verdelingen (over simulatieronden heen) en zetten deze uit in een plot.
- Verder berekenen we per simulatieronde en model de gerealiseerde fractie imputaties die exact gelijk zijn aan de juiste categorie of daar maximaal één categorie naast zitten (corresponderend met de maten κ0 en κ1, maar nu als gesimuleerde fracties in plaats van de theoretische verwachting). Per model berekenen we het gemiddelde en de standaardfout van deze gemiddelde fracties (over simulatieronden heen). Ook kijken we naar het verschil tussen deze fracties voor elk model ten opzichte van het huidige imputatiemodel, en naar de verschillen tussen opeenvolgende modellen qua complexiteit.
- Van de berekende onderwijsscores gebaseerd op de imputaties maken we per model een plot van de verdeling van de gevonden afwijkingen ten opzichte van de scores waarbij opleidingsniveau niet is geïmputeerd.
Bij het berekenen van deze maten maken we onderscheid tussen deelpopulaties waarbij alleen de vader, alleen de moeder, of beide ouders geïmputeerde opleidingsniveaus hebben. Verder bekijken we de maten bij onderdeel 1 ook voor deelpopulaties van kinderen van verschillende leeftijden.
Het imputatiemodel dat gemiddeld de kleinste afwijkingen geeft t.o.v. de situatie zonder verwijderde waarden heeft de voorkeur. Als de resultaten van 1, 2 en 3 niet eenduidig zijn, is een betere prestatie bij 3 in principe belangrijker dan een betere prestatie bij 1 en 2.
Validatiestudie
Voor de validatiestudie maken we gebruik van de verzameling V van ouders voor wie het opleidingsniveau ontbreekt in het bestand van 2021 maar is waargenomen in het bestand van 2022. De aanname hierbij is dat het opleidingsniveau van deze ouders uit het bestand van 2022 een goede proxywaarneming is voor hun opleidingsniveau in 2021.
Dezelfde imputatiemodellen als in de simulatiestudie zijn onderzocht. Voor deze validatiestudie zijn deze modellen toegepast op het bestand van 2021 met de ontbrekende waarden die in werkelijkheid voorkomen in dat bestand. Zoals gebruikelijk worden er J=10 imputaties per persoon gemaakt. Na afloop wordt de kwaliteit van de imputaties geëvalueerd op alleen de deelverzameling V.
Een probleem met deze validatiestudie is dat de deelverzameling V geen representatieve steekproef is uit alle ouders met onbekende opleidingsniveaus in 2021. Uit een verkennende analyse bleek dat dit een selectieve groep ouders is naar een aantal achtergrondkenmerken en dat bovendien de bestaande ophooggewichten uit het Opleidingsniveaubestand van 2021 niet volledig kunnen corrigeren voor deze selectiviteit. Er is daarom, voor de drie deelpopulaties A, B en C apart, een herweging uitgevoerd via lineair wegen (Bethlehem, 2007). Na deze herweging heeft de deelverzameling V voor zowel moeders als vaders exact dezelfde (gewogen) verdeling als de hele populatie voor de volgende kenmerken:
- opleidingsniveau andere ouder [8] (alleen bij deelpopulaties B en C)
- inkomen ouder [21]
- herkomstgroepering ouder [8]
- type economische activiteit werkgever ouder [12]
- leeftijd ouder [5]
Deze kenmerken zijn gekozen omdat ze in de stepwise-analyse naar voren kwamen als de kenmerken die het sterkst samenhangen met opleidingsniveau.
We berekenen vergelijkbare evaluatiematen als bij de simulatiestudie:
- Per model berekenen we de gemiddelde geïmputeerde verdeling van opleidingsniveau bij de ouders in deelverzameling V en vergelijken deze met de werkelijke verdeling voor deze ouders (zoals waargenomen in 2022). Hierbij wordt rekening gehouden met de gewichten na de herweging die hierboven is beschreven. Per model berekenen we het gemiddelde en de standaardfout van de afwijking tussen de twee verdelingen. Voor het bepalen van de standaardfout is er in dit geval, anders dan bij de simulatiestudie, geen herhaalde simulatie beschikbaar. In plaats daarvan berekenen we de variantieschatting \(\widehat{var}\left( {\overline{\widehat{P}}}_{imp,cJ} - {\widehat{P}}_{c} \right)\) die wordt afgeleid in Bijlage 3.
- Verder berekenen we per model de gerealiseerde fractie imputaties die exact gelijk zijn aan de juiste categorie of daar maximaal één categorie naast zitten.
- Van de berekende onderwijsscores gebaseerd op de imputaties maken we per model een plot van de verdeling van de gevonden afwijkingen ten opzichte van de scores waarbij opleidingsniveau niet is geïmputeerd.
Bij het berekenen van deze maten maken we wederom onderscheid tussen de subgroepen waarbij alleen de vader, alleen de moeder, of beide ouders een geïmputeerd opleidingsniveau hebben. Ook bekijken we de evaluatiematen bij onderdeel 1 wederom voor deelpopulaties van kinderen van verschillende leeftijden.
3.3 Resultaten
3.3.1 Imputatie hulpvariabelen
De resultaten lieten zien dat het gebruik van donorimputatie bij een grote dataset, met het gebruik van veel achtergrondkenmerken aanloopt tegen geheugenproblemen. Zo moet er bij een methode als KNN voor elke persoon met ontbrekende waarden, een afstandsscore worden berekend tot de andere donoren in het bestand. Dit aantal loopt al snel op bij een grote dataset, waardoor een grote hoeveelheid informatie moet worden opgeslagen in het geheugen. Dit zal ook net zoals bij de predictive mean matching invloed kunnen hebben op de snelheid. Voor de huidige toepassing zijn deze methoden daarom minder geschikt.
De beslisboomtechnieken kunnen sneller werken omdat het maar eenmalig toegepast hoeft te worden op de dataset voor de groep donoren. Hierbij bleek een random forest model de snelste methode. Omdat de random forest methode zowel inhoudelijk past bij ons imputatiedoel (het imputeren van categorische en continue variabelen) en de snelste is binnen mice, zijn we verder gegaan met dit model voor de imputatie van de achtergrondkenmerken.
De snelheid van de methoden zijn eerst getest op een willekeurige steekproef van 100.000 uit de populatie bij de moeders en vaders. De volgende stap was het toepassen van het random forest model met mice op de gehele populatie voor de moeders en vaders. De huidige imputatie met mice bestond uit tien iteraties. We hebben daarbij ook getest of tien iteraties noodzakelijk is voor de random forest of dat minder interaties ook volstaat.
Om de imputatie voor burgerlijke staat, persoonlijk inkomen en de sociaal-economische categorie met de nieuwe methode te beoordelen, maken we twee vergelijkingen:
- We bekijken de stabiliteit van de uitkomsten door telkens per ouder twee datasets te imputeren. Per kenmerk, zoals burgerlijke staat, bekijken we dan per geïmputeerde categorie, hoe deze verdeeld is in de imputaties voor de twee datasets. Op basis van het percentage wat overlapt over de twee imputatieronden, kunnen we dan de stabiliteit beoordelen. Daarnaast kunnen we zien of de categorieën die verschillen, ook inhoudelijk aan elkaar verwant zijn, of overduidelijk verkeerd zijn. Hoe hoger het percentage overlap, hoe stabieler de imputatie is. Voor het persoonlijk inkomen hebben we de imputatie ingedeeld in categorieën om eenzelfde vergelijking te kunnen maken.
- We bekijken de verschillen tussen de oude methode (mice – pmm) en de nieuwe methode (mice – rf). Dit doen we door de frequentieverdeling van de kenmerken te vergelijken voor en na imputatie. Op persoonsniveau kan de imputatie wel variëren, maar op geaggregeerd niveau zou je verwachten dat de totale verdeling over de categorieën ongeveer gelijk blijft. Daarnaast bekijken we het verschil in de frequentieverdeling voor de oude en nieuwe methode. Hierin wil je vooral een methode die het dichtst bij de verdeling in de originele data blijft. Maar je wilt ook dat de methoden onderling niet sterk afwijken, wat zou aanduiden dat de imputaties niet stabiel zijn over verschillende methoden heen. Ook maken we een vergelijking van de verdeling over de geïmputeerde categorieën tussen de oude en nieuwe methoden, om de stabiliteit te beoordelen.
De resultaten lieten zien dat de random forest methode aanzienlijk sneller is op de totale populatie dan de oude methode. Daarnaast zien we dat de frequentieverdeling stabiel blijft voor de imputatie met zowel één als tien iteraties als over twee imputatieronden heen.
Na de keuze voor het nieuwe model, hebben we het model uitgebreid door extra achtergrondkenmerken toe te voegen aan de imputatie. We bekijken daarbij eerst of we de achtergrondkenmerken van de andere ouder mee kunnen nemen. Omdat de andere ouder niet altijd bekend is, geven we het model ook een kenmerk mee wat aangeeft of de andere ouder wel of niet in de BRP zit. Op deze manier geven we toch extra informatie mee over de groep die wel bekend is en niet bekend is. De kenmerken van die andere ouder die niet bekend is, zullen dan ook ontbreken. In dat geval zal mice ook die ontbrekende waarden imputeren. Omdat de kenmerken voor een groot deel van de andere ouders wel bekend zijn, zal dit toch voldoende informatie kunnen toevoegen om een bijdrage te leveren aan het imputatiemodel.
De resultaten worden weer vergeleken op de stabiliteit en met de methode waarbij alleen de kenmerken van de ouder zelf worden meegenomen. Hierin zien we een verbetering van het percentage overlap. Daarnaast zijn de categorieën die niet overlappen nu vaker inhoudelijk aan elkaar verwant dan voorheen.
Tot slot hebben we ook nog onderzocht of we het imputatiemodel nog kunnen uitbreiden met het opleidingsniveau van de ouder en/of andere ouder. In de gevallen dat we deze informatie wel hebben, kan dit ook weer een toegevoegde bijdrage leveren aan het imputatiemodel. De ontbrekende waarden zullen ook automatisch geïmputeerd worden door mice. Ook deze resultaten lieten zien dat de stabiliteit verbeterde na het toevoegen van het opleidingsniveau.
Voor de variabele burgerlijke staat van de moeder hebben we het totale effect geïllustreerd in de figuren 3.3.1. (huidige situatie) en 3.3.2 (implementatie alle beschreven wijzigingen). In de huidige situatie wordt in 2 opvolgende imputaties ongeveer 43 procent dezelfde waarde geïmputeerd. Na het toepassen van alle verbeteringen stijgt dit tot 67 procent. Voor de variabele burgerlijke staat was de verbetering van de stabiliteit het sterkst. Bij de overige variabelen was de verbetering minder sterk. Bij geen van de variabelen trad een verslechtering op.
3.3.2 Regressiemethodiek opleidingsniveau
Beide imputatiemodellen (multinomiale en continuation-ratio logistische regressie) zijn toegepast op hetzelfde bestand, namelijk het bestand waarmee de indicator voor 2022 is geproduceerd. Er is gekeken naar de volgende uitkomstmaten:
a. gemiddelde en standaarddeviatie (over 10 imputatieronden) van de verdeling van
opleidingsniveau vader of moeder na imputatie;
b. verdeling van onderwijsscores berekend op basis van geïmputeerde data;
c. verdeling verschillen tussen onderwijsscores berekend op basis van geïmputeerde data
met verschillende methoden:
– correlatie;
– heatmap van verschillen tussen scores (naar beneden afgerond op geheel getal);
– staafdiagram van grootte van verschillen tussen scores.
De uitkomstmaten bij (b) en (c) zijn zowel berekend op alle data als op alleen de data van kinderen bij wie het opleidingsniveau van ten minste één ouder wordt geïmputeerd. Verder is, ter vergelijking, de huidige methode (op basis van continuation-ratio logistische regressie) twee keer onafhankelijk toegepast.
Bij alle uitkomstmaten was de conclusie steeds dat de verschillen die we zien tussen de twee verschillende modellen van een vergelijkbare omvang zijn als die bij herhaalde toepassing van het huidige model. Dat wil zeggen: veranderen van imputatiemethode leidt tot verschillen in de geïmputeerde waarden die niet groter zijn dan wat men zou zien als de huidige imputatiemethode twee keer onafhankelijk wordt uitgevoerd. In dit opzicht zou het overstappen op multinomiale logistische regressie een kleine impact hebben op de resultaten: de verschillen vallen binnen de ‘normale imputatieruis’ van de bestaande methode.
Verder was te zien dat de verdelingen na imputatie bij multinomiale logistische regressie niet systematisch afwijken van de verdeling bij continuation-ratio logistische regressie. Met name bij de moeders was te zien dat de relatief grootste afwijkingen voorkomen bij de hoogste opleidingsniveaus. Vanwege de manier waarop het continuation-ratio-model geschat wordt, is het aannemelijk dat de imputaties voor hogere opleidingsniveaus bij dit model minder nauwkeurig zijn dan de imputaties voor lagere opleidingsniveaus. Dat de verschillen tussen de methoden relatief groot waren bij de hoogste opleidingsniveaus is plausibel in het licht van deze aanname. Dit zou bovendien een aanwijzing kunnen zijn dat de imputaties bij multinomiale logistische regressie voor de hoogste opleidingsniveaus nauwkeuriger zijn dan bij de huidige methode.
3.3.3 Imputatie opleidingsniveau
Selectie van achtergrondkenmerken
Deze analyse is eenmaal uitgevoerd voor alle vaders of moeders met bekende opleidingsniveaus en eenmaal voor alleen de ouderparen met beide opleidingsniveaus bekend. Het kenmerk ‘opleidingsniveau andere ouder’ is alleen meegenomen bij deze tweede groep. Deze tweede analyse is relevant voor het imputeren van onbekende waarden als het opleidingsniveau van de andere ouder beschikbaar is, de eerste analyse is relevant voor het imputeren als beide opleidingsniveaus onbekend zijn. De uiteindelijk gekozen imputatiemodellen mogen voor beide situaties verschillen.
Tabel 3.3.3 en 3.3.4 tonen de uitkomsten van de analyses voor de eerste groep, tabel 3.3.5 en 3.3.6 voor de tweede groep. Kenmerken/indelingen die gemarkeerd zijn, zijn behouden voor het vervolg (de stepwise-analyse). De niet-gekozen indelingen leidden niet tot een duidelijke verbetering ten opzichte van de gekozen indelingen. Het enige kenmerk dat in deze fase geheel is afgevallen is de leeftijd van het kind, aangezien dit kenmerk geen meerwaarde bleek te hebben boven de leeftijd van de ouder zelf.
| Variabele | Selectie | AIC | E(κ0) | E(κ1) |
|---|---|---|---|---|
| Alleen constante | 14906983,6 | 0,1623 | 0,3793 | |
| Leeftijd moeder [5*] | S | 14740694,6 | 0,1681 | 0,3882 |
| Leeftijd moeder [8] | 14725961,8 | 0,1686 | 0,3884 | |
| Leeftijd moeder [in jaren] | 14816131,0 | 0,1650 | 0,3818 | |
| Burgerlijke staat moeder [3*] | 14826593,6 | 0,1649 | 0,3840 | |
| Burgerlijke staat moeder [4] | S | 14824399,4 | 0,1650 | 0,3841 |
| Herkomstgroepering moeder [8*] | S | 14322913,1 | 0,1831 | 0,4083 |
| Inkomen moeder [4*] | S | 13488710,1 | 0,2140 | 0,4755 |
| Inkomen moeder [5] | 13470075,0 | 0,2156 | 0,4753 | |
| Inkomen moeder [6] | S | 13346684,3 | 0,2215 | 0,4826 |
| Inkomen moeder [11] | S | 13227184,0 | 0,2277 | 0,4887 |
| Inkomen moeder [21] | S | 13172711,1 | 0,2306 | 0,4919 |
| Inkomen moeder [continu] | 13516276,9 | 0,2142 | 0,4713 | |
| Welvaart huishouden [5] | S | 14041453,8 | 0,1944 | 0,4371 |
| Welvaart huishouden [6] | 14012920,9 | 0,1956 | 0,4386 | |
| Welvaart huishouden [11] | S | 13967297,8 | 0,1975 | 0,4411 |
| Welvaart huishouden [21] | S | 13919176,5 | 0,1992 | 0,4442 |
| Sociaaleconomische categorie moeder [2*] | S | 14359812,6 | 0,1802 | 0,4122 |
| Sociaaleconomische categorie moeder [13] | S | 14149862,2 | 0,1887 | 0,4249 |
| Type economische activiteit werkgever | ||||
| moeder [12] | S | 14057107,1 | 0,1901 | 0,4290 |
| Deeltijdfactor werk moeder [5] | S | 14147939,0 | 0,1884 | 0,4255 |
| Deeltijdfactor werk moeder [6] | 14152732,2 | 0,1882 | 0,4246 | |
| Deeltijdfactor werk moeder [11] | S | 14128718,6 | 0,1892 | 0,4259 |
| Stedelijkheidsgraad buurt [6*] | S | 14789235,7 | 0,1662 | 0,3824 |
| Leeftijd kind [in jaren] | 14755577,2 | 0,1668 | 0,3851 | |
| Variabele | Selectie | AIC | E(κ0) | E(κ1) |
|---|---|---|---|---|
| Alleen constante | 13181728,0 | 0,1614 | 0,3851 | |
| Leeftijd vader [5*] | S | 13053641,0 | 0,1672 | 0,3942 |
| Leeftijd vader [8] | 13040331,4 | 0,1677 | 0,3946 | |
| Leeftijd vader [in jaren] | 13088529,7 | 0,1650 | 0,3902 | |
| Burgerlijke staat vader [3*] | 13140265,5 | 0,1630 | 0,3881 | |
| Burgerlijke staat vader [4] | S | 13139959,5 | 0,1630 | 0,3882 |
| Herkomstgroepering vader [8*] | S | 12715446,4 | 0,1785 | 0,4128 |
| Inkomen vader [4*] | S | 11968938,2 | 0,2112 | 0,4798 |
| Inkomen vader [5] | 12364547,4 | 0,1937 | 0,4469 | |
| Inkomen vader [6] | S | 12181841,1 | 0,2020 | 0,4637 |
| Inkomen vader [11] | S | 11926443,5 | 0,2134 | 0,4834 |
| Inkomen vader [21] | S | 11840266,8 | 0,2183 | 0,4879 |
| Inkomen vader [continu] | 12083656,5 | 0,2051 | 0,4679 | |
| Welvaart huishouden [5] | S | 12454769,0 | 0,1919 | 0,4399 |
| Welvaart huishouden [6] | 12425657,8 | 0,1933 | 0,4417 | |
| Welvaart huishouden [11] | S | 12375915,1 | 0,1958 | 0,4446 |
| Welvaart huishouden [21] | S | 12332717,6 | 0,1978 | 0,4477 |
| Sociaaleconomische categorie vader [2*] | S | 12919262,8 | 0,1711 | 0,4029 |
| Sociaaleconomische categorie vader [13] | S | 12746566,2 | 0,1788 | 0,4146 |
| Type economische activiteit werkgever | ||||
| vader [12] | S | 12305263,2 | 0,1969 | 0,4521 |
| Deeltijdfactor werk vader [5] | S | 12883572,9 | 0,1721 | 0,4042 |
| Deeltijdfactor werk vader [6] | 12891954,7 | 0,1719 | 0,4036 | |
| Deeltijdfactor werk vader [11] | S | 12877831,3 | 0,1725 | 0,4048 |
| Stedelijkheidsgraad buurt [6*] | S | 13063363,0 | 0,1660 | 0,3884 |
| Leeftijd kind [in jaren] | 13148700,4 | 0,1624 | 0,3862 | |
| Variabele | Selectie | AIC | E(κ0) | E(κ1) |
|---|---|---|---|---|
| Alleen constante | 10681952,8 | 0,1719 | 0,3954 | |
| Opleidingsniveau vader [8*] | S | 9397405,2 | 0,2432 | 0,5126 |
| Leeftijd moeder [5*] | S | 10523154,2 | 0,1798 | 0,4082 |
| Leeftijd moeder [8] | 10512707,8 | 0,1803 | 0,4085 | |
| Leeftijd moeder [in jaren] | 10594659,0 | 0,1756 | 0,3998 | |
| Burgerlijke staat moeder [3*] | 10629956,8 | 0,1741 | 0,3992 | |
| Burgerlijke staat moeder [4] | S | 10629794,3 | 0,1741 | 0,3992 |
| Herkomstgroepering moeder [8*] | S | 10267050,5 | 0,1911 | 0,4227 |
| Inkomen moeder [4*] | S | 9579981,5 | 0,2284 | 0,4969 |
| Inkomen moeder [5] | 9564547,1 | 0,2304 | 0,4967 | |
| Inkomen moeder [6] | S | 9475028,1 | 0,2367 | 0,5035 |
| Inkomen moeder [11] | S | 9388746,3 | 0,2432 | 0,5091 |
| Inkomen moeder [21] | S | 9348504,2 | 0,2461 | 0,5122 |
| Inkomen moeder [continu] | 9603157,8 | 0,2285 | 0,4920 | |
| Welvaart huishouden [5] | S | 9966883,3 | 0,2091 | 0,4608 |
| Welvaart huishouden [6] | 9942577,6 | 0,2106 | 0,4625 | |
| Welvaart huishouden [11] | S | 9904527,9 | 0,2128 | 0,4654 |
| Welvaart huishouden [21] | S | 9869388,9 | 0,2146 | 0,4685 |
| Sociaaleconomische categorie moeder [2*] | S | 10271129,6 | 0,1896 | 0,4281 |
| Sociaaleconomische categorie moeder [13] | S | 10121420,9 | 0,1984 | 0,4408 |
| Type economische activiteit werkgever | ||||
| moeder [12] | S | 10053796,6 | 0,1996 | 0,4454 |
| Deeltijdfactor werk moeder [5] | S | 10102008,1 | 0,1991 | 0,4430 |
| Deeltijdfactor werk moeder [6] | 10107260,1 | 0,1988 | 0,4418 | |
| Deeltijdfactor werk moeder [11] | S | 10086733,4 | 0,2002 | 0,4433 |
| Stedelijkheidsgraad buurt [6*] | S | 10595742,0 | 0,1758 | 0,3985 |
| Leeftijd kind [in jaren] | 10573179,1 | 0,1759 | 0,4004 | |
| Variabele | Selectie | AIC | E(κ0) | E(κ1) |
|---|---|---|---|---|
| Alleen constante | 10830481,9 | 0,1632 | 0,3873 | |
| Opleidingsniveau moeder [8*] | S | 9545934,3 | 0,2327 | 0,5016 |
| Leeftijd vader [5*] | S | 10694950,8 | 0,1706 | 0,3991 |
| Leeftijd vader [8] | 10685288,6 | 0,1711 | 0,3995 | |
| Leeftijd vader [in jaren] | 10731134,6 | 0,1680 | 0,3941 | |
| Burgerlijke staat vader [3*] | 10788264,1 | 0,1653 | 0,3909 | |
| Burgerlijke staat vader [4] | S | 10788234,6 | 0,1653 | 0,3910 |
| Herkomstgroepering vader [8*] | S | 10453133,6 | 0,1797 | 0,4143 |
| Inkomen vader [4*] | S | 9807622,1 | 0,2149 | 0,4841 |
| Inkomen vader [5] | 10129236,4 | 0,1970 | 0,4519 | |
| Inkomen vader [6] | S | 9979488,6 | 0,2054 | 0,4687 |
| Inkomen vader [11] | S | 9769592,2 | 0,2171 | 0,4881 |
| Inkomen vader [21] | S | 9697800,1 | 0,2224 | 0,4927 |
| Inkomen vader [continu] | 9894364,5 | 0,2092 | 0,4730 | |
| Welvaart huishouden [5] | S | 10166966,8 | 0,1976 | 0,4485 |
| Welvaart huishouden [6] | 10141294,6 | 0,1992 | 0,4504 | |
| Welvaart huishouden [11] | S | 10099224,3 | 0,2019 | 0,4534 |
| Welvaart huishouden [21] | S | 10063916,3 | 0,2038 | 0,4564 |
| Sociaaleconomische categorie vader [2*] | S | 10598106,3 | 0,1735 | 0,4063 |
| Sociaaleconomische categorie vader [13] | S | 10458999,0 | 0,1810 | 0,4178 |
| Type economische activiteit werkgever | ||||
| vader [12] | S | 10081898,5 | 0,2004 | 0,4571 |
| Deeltijdfactor werk vader [5] | S | 10566704,6 | 0,1746 | 0,4077 |
| Deeltijdfactor werk vader [6] | 10573936,6 | 0,1743 | 0,4072 | |
| Deeltijdfactor werk vader [11] | S | 10560012,5 | 0,1750 | 0,4085 |
| Stedelijkheidsgraad buurt [6*] | S | 10731617,0 | 0,1679 | 0,3908 |
| Leeftijd kind [in jaren] | 10790578,0 | 0,1647 | 0,3890 | |
Vervolgens is, voor moeder en vader apart, een forward stepwise-analyse uitgevoerd, wederom op basis van alleen de ouders met bekende opleidingsniveaus, met de geselecteerde kenmerken (een S in de kolom ‘selectie’) uit tabel 3.3.3 tot en met 3.3.6 als mogelijke hulpvariabelen om uit te kiezen. Tijdens deze analyse worden multinomiale logistische regressiemodellen geschat. In elke ronde wordt steeds het kenmerk toegevoegd dat leidt tot de grootste verbetering van de AIC-waarde, totdat er geen verbetering in AIC-waarde meer optreedt. Om de rekentijd te beperken zijn in deze analyse alleen de ouders meegenomen voor wie het opleidingsniveau in de EBB is waargenomen, terwijl bij het schatten van de modellen rekening is gehouden met de ophooggewichten uit het Opleidingsniveaubestand.
Ook deze analyse is tweemaal uitgevoerd: eenmaal voor alle vaders of moeders met bekende opleidingsniveaus en eenmaal voor alleen de ouderparen met beide opleidingsniveaus bekend, waarbij voor die laatste groep ook het kenmerk ‘opleidingsniveau andere ouder’ is meegenomen. Tabel 3.3.7 en 3.3.8 tonen de uitkomsten voor de eerste groep, tabel 3.3.9 en 3.3.10 voor de tweede groep.
| stap | model | df | AIC |
|---|---|---|---|
| 1 | alleen constante | 7 | 6246197,7 |
| 2 | 1 + inkomen moeder [21] | 140 | 5860071,2 |
| 3 | 2 + herkomstgroepering moeder [8*] | 49 | 5560602,4 |
| 4 | 3 + type economische activiteit werkgever moeder [12] | 77 | 5475840,0 |
| 5 | 4 + welvaart huishouden [21] | 140 | 5439609,6 |
| 6 | 5 + leeftijd moeder [5*] | 28 | 5411758,9 |
| 7 | 6 + sociaaleconomische categorie moeder [13] | 84 | 5391979,0 |
| 8 | 7 + deeltijdfactor werk moeder [11] | 63 | 5374429,2 |
| 9 | 8 + stedelijkheidsgraad buurt [6*] | 35 | 5357229,0 |
| 10 | 9 + burgerlijke staat moeder [4] | 21 | 5352360,2 |
| 11 | 10 + inkomen moeder [4*] | 21 | 5348643,3 |
| 12 | 11 + deeltijdfactor werk moeder [5] | 14 | 5348159,1 |
| stap | model | df | AIC |
|---|---|---|---|
| 1 | alleen constante | 7 | 6902311,9 |
| 2 | 1 + inkomen vader [21] | 140 | 6559602,7 |
| 3 | 2 + herkomstgroepering vader [8*] | 49 | 6329333,3 |
| 4 | 3 + type economische activiteit werkgever vader [12] | 77 | 6135087,0 |
| 5 | 4 + leeftijd vader [5*] | 28 | 6085007,3 |
| 6 | 5 + welvaart huishouden [21] | 140 | 6053999,5 |
| 7 | 6 + sociaaleconomische categorie vader [13] | 77 | 6027150,2 |
| 8 | 7 + stedelijkheidsgraad buurt [6*] | 35 | 6002161,8 |
| 9 | 8 + deeltijdfactor werk vader [11] | 63 | 5987212,4 |
| 10 | 9 + inkomen vader [4*] | 21 | 5979859,2 |
| 11 | 10 + burgerlijke staat vader [4] | 21 | 5977025,6 |
| 12 | 11 + deeltijdfactor werk vader [5] | 14 | 5976284,2 |
| stap | model | df | AIC |
|---|---|---|---|
| 1 | alleen constante | 7 | 5490300,0 |
| 2 | 1 + opleidingsniveau vader [8*] | 49 | 5146998,2 |
| 3 | 2 + inkomen moeder [21] | 140 | 4884665,2 |
| 4 | 3 + herkomstgroepering moeder [8*] | 49 | 4692281,5 |
| 5 | 4 + type economische activiteit werkgever moeder [12] | 77 | 4634321,3 |
| 6 | 5 + leeftijd moeder [5*] | 28 | 4606179,7 |
| 7 | 6 + welvaart huishouden [21] | 140 | 4588531,4 |
| 8 | 7 + deeltijdfactor werk moeder [11] | 63 | 4575446,2 |
| 9 | 8 + sociaaleconomische categorie moeder [13] | 70 | 4563273,1 |
| 10 | 9 + stedelijkheidsgraad buurt [6*] | 35 | 4554583,7 |
| 11 | 10 + inkomen moeder [4*] | 21 | 4552206,9 |
| 12 | 11 + burgerlijke staat moeder [4] | 21 | 4549987,4 |
| 13 | 12 + deeltijdfactor werk moeder [5] | 14 | 4549384,4 |
| stap | model | df | AIC |
|---|---|---|---|
| 1 | alleen constante | 7 | 6377786,2 |
| 2 | 1 + opleidingsniveau moeder [8*] | 49 | 5985374,1 |
| 3 | 2 + inkomen vader [21] | 140 | 5745312,3 |
| 4 | 3 + type economische activiteit werkgever vader [12] | 77 | 5596804,9 |
| 5 | 4 + herkomstgroepering vader [8*] | 49 | 5472270,9 |
| 6 | 5 + leeftijd vader [5*] | 28 | 5420651,1 |
| 7 | 6 + sociaaleconomische categorie vader [13] | 77 | 5398554,1 |
| 8 | 7 + stedelijkheidsgraad buurt [6*] | 35 | 5382453,1 |
| 9 | 8 + welvaart huishouden [21] | 140 | 5368744,6 |
| 10 | 9 + deeltijdfactor werk vader [11] | 63 | 5359711,5 |
| 11 | 10 + inkomen vader [4*] | 21 | 5354488,6 |
| 12 | 11 + burgerlijke staat vader [4] | 21 | 5350848,4 |
| 13 | 12 + deeltijdfactor werk vader [5] | 14 | 5350239,3 |
De resultaten in tabellen 3.3.9 en 3.3.10 bevestigen dat het opleidingsniveau van de andere ouder, indien beschikbaar, het beste kenmerk is om opleidingsniveau te modelleren (zoals was aangenomen in de huidige imputatiemethode). Het inkomen van de ouder zelf is het kenmerk dat daarna de meeste voorspelkracht heeft.
Op basis van de uitkomsten van de stepwise-analyses is besloten om de volgende modellen te testen in een verdere simulatie- en validatiestudie. Per deelpopulatie worden hieronder het kleinste en grootste model weergegeven dat is getest. Alle tussenliggende modellen waarbij steeds één extra term wordt toegevoegd, in de volgorde uit de stepwise-analyse, zijn ook getest.
- Deelpopulatie C (moeders):
- KLEINSTE MODEL:
opleidingsniveau vader [8] × (inkomen moeder [21]) - GROOTSTE MODEL:
opleidingsniveau moeder [8] × (inkomen vader [21] + type economische activiteit werkgever vader [12] + herkomstgroepering vader [8] + leeftijd vader [5] + sociaaleconomische categorie vader [13] + stedelijkheidsgraad buurt [6] + welvaart huishouden [21] + deeltijdfactor werk vader [11] + burgerlijke staat vader [4] + deeltijdfactor werk vader [5]) - Deelpopulatie B (vaders):
- KLEINSTE MODEL:
opleidingsniveau moeder [8] × (inkomen vader [21]) - GROOTSTE MODEL:
opleidingsniveau moeder [8] × (inkomen vader [21] + type economische activiteit werkgever vader [12] + herkomstgroepering vader [8] + leeftijd vader [5] + sociaaleconomische categorie vader [13] + stedelijkheidsgraad buurt [6] + welvaart huishouden [21] + deeltijdfactor werk vader [11] + burgerlijke staat vader [4] + deeltijdfactor werk vader [5]) - Deelpopulatie A (moeders):
- KLEINSTE MODEL:
inkomen moeder [21] × (herkomstgroepering moeder [8]) - GROOTSTE MODEL:
inkomen moeder [21] × (herkomstgroepering moeder [8] + type economische activiteit werkgever moeder [12] + welvaart huishouden [21] + leeftijd moeder [5] + sociaaleconomische categorie moeder [13] + deeltijdfactor werk moeder [11] + stedelijkheidsgraad buurt [6] + burgerlijke staat moeder [4] + deeltijdfactor werk moeder [5]) - Deelpopulatie A (vaders):
dezelfde modellen als bij deelpopulatie B
Simulatiestudie
De figuren 3.3.11 en 3.3.12 tonen het verschil tussen de geïmputeerde verdeling en echte verdeling van het opleidingsniveau van de moeder. In de kolommen is onderscheid gemaakt tussen de situatie waarbij alleen opleidingsniveau van de moeder wordt geïmputeerd (3.3.11) en waarbij opleidingsniveau van beide ouders wordt geïmputeerd (3.3.12). Elk punt vertegenwoordigt een imputatiemodel, waarbij model 1 het meest eenvoudige model is en model 10 het meest uitgebreide model. De foutenbalk rond een punt is gebaseerd op de spreiding over de simulatieronden heen. Dat de spreiding groter is bij de groep met beide opleidingsniveaus onbekend komt vooral doordat de steekproefomvang bij deze groep relatief klein is, vanwege de manier waarop de aanvullende ontbrekende waarden zijn gesimuleerd.
De geschatte verdelingen op basis van de verschillende imputatiemodellen liggen niet ver uit elkaar. Specifiek voor de uitsplitsing naar leeftijd van het kind is een duidelijke verbetering te zien op het moment dat de leeftijd van de moeder wordt opgenomen in het model (model 4 versus model 3). Daarna blijven de uitkomsten redelijk stabiel. De figuren 3.3.13 en 3.3.14 tonen vergelijkbare uitkomsten voor het imputeren van het opleidingsniveau van de vader.
Tabel 3.3.15 tot en met 3.3.18 tonen uitkomsten met betrekking tot de gerealiseerde fractie imputaties die exact gelijk zijn aan de juiste categorie of daar maximaal één categorie naast zitten (κ0 en κ1). Tabel 3.3.15 gaat over de maat κ0 voor imputaties bij moeders. De derde kolom toont de gemiddelde waarde van κ0 over simulatieronden heen. De vierde kolom toont het verschil tussen de gemiddelde κ0 bij een bepaald model en het huidige model; de zesde kolom toont het verschil tussen de gemiddelde κ0 bij een bepaald model en het direct voorafgaande model qua complexiteit. In de kolommen vijf en zeven zijn waarden met een ‘S’gemarkeerd als zij positief zijn en minimaal twee keer zo groot als de bijbehorende standaardfout over simulatieronden heen. Dat wil zeggen: een gemakeerde waarde in de vierde of zesde kolom geeft aan dat een bepaald model een significante verbetering geeft ten opzichte van het huidige model of het voorafgaande model qua complexiteit. De tabellen 3.3.16, 3.3.17 en 3.3.18 zijn op dezelfde manier opgebouwd. Te zien is dat alle voldoende complexe modellen een significante verbetering in κ0 en κ1 laten zien ten opzichte van het huidige model, zowel bij moeders als bij vaders. De meest complexe modellen geven echter geen significante verbetering meer ten opzichte van de voorafgaande, iets minder complexe modellen.
Afgaand op dit laatste criterium lijkt bij moeders model 7 een goed compromis te zijn tussen complexiteit van het model en nauwkeurigheid van de imputaties als het opleidingsniveau van beide ouders onbekend is. Als het opleidingsniveau van de vader wel bekend is scoren model 8 en 9 nog iets beter met betrekking tot maat κ0 (wel significant) en maat κ1 (niet significant). Bij vaders zijn de resultaten minder eenduidig. Hier lijkt model 8 een redelijk compromis als het opleidingsniveau van de moeder wel bekend is. Als het opleidingsniveau van de moeder niet bekend is, treedt nog wel een duidelijke verbetering op tot en met model 7, al is deze verbetering niet altijd statistisch significant.
| Deel-populatie1) | κ0 (gem.) | Δκ0 huidig (gem.) | Signifi-cantie2) | Δκ0 cumulatief (gem.) | Signifi-cantie2) |
|---|---|---|---|---|---|
| C huidig | 0,2426 | ||||
| C1 | 0,2327 | -0,0099 | |||
| C2 | 0,2422 | -0,0004 | 0,0095 | S | |
| C3 | 0,2505 | 0,0079 | S | 0,0083 | S |
| C4 | 0,2552 | 0,0125 | S | 0,0046 | S |
| C5 | 0,2576 | 0,0149 | S | 0,0024 | S |
| C6 | 0,2593 | 0,0167 | S | 0,0017 | S |
| C7 | 0,2612 | 0,0186 | S | 0,0019 | S |
| C8 | 0,2626 | 0,0200 | S | 0,0014 | S |
| C9 | 0,2637 | 0,0211 | S | 0,0011 | S |
| C10 | 0,2629 | 0,0203 | S | -0,0008 | |
| A huidig | 0,2123 | ||||
| A1 | 0,2134 | 0,0012 | |||
| A2 | 0,2237 | 0,0114 | S | 0,0102 | S |
| A3 | 0,2288 | 0,0165 | S | 0,0051 | S |
| A4 | 0,2339 | 0,0217 | S | 0,0051 | S |
| A5 | 0,2399 | 0,0276 | S | 0,0060 | S |
| A6 | 0,2464 | 0,0342 | S | 0,0065 | S |
| A7 | 0,2491 | 0,0369 | S | 0,0027 | S |
| A8 | 0,2503 | 0,0381 | S | 0,0012 | |
| A9 | 0,2504 | 0,0381 | S | 0,0001 | |
| 1) C = alleen moeder onbekend, A = vaders en moeders onbekend. De getallen duiden de modellen aan. 2) Het verschil is positief en minimaal twee keer zo groot als de bijbehorende standaardfout. | |||||
| Deel-populatie1) | κ1 (gem.) | Δκ1 huidig (gem.) | Signifi-cantie2) | Δκ1 cumulatief (gem.) | Signifi-cantie2) |
|---|---|---|---|---|---|
| C huidig | 0,5331 | ||||
| C1 | 0,5219 | -0,0111 | |||
| C2 | 0,5304 | -0,0027 | 0,0085 | S | |
| C3 | 0,5397 | 0,0067 | S | 0,0094 | S |
| C4 | 0,5451 | 0,0121 | S | 0,0054 | S |
| C5 | 0,5479 | 0,0148 | S | 0,0027 | S |
| C6 | 0,5507 | 0,0177 | S | 0,0029 | S |
| C7 | 0,5541 | 0,0210 | S | 0,0033 | S |
| C8 | 0,5549 | 0,0218 | S | 0,0008 | |
| C9 | 0,5559 | 0,0228 | S | 0,0010 | |
| C10 | 0,5558 | 0,0227 | S | -0,0001 | |
| A huidig | 0,4864 | ||||
| A1 | 0,4860 | -0,0004 | |||
| A2 | 0,4947 | 0,0082 | S | 0,0087 | |
| A3 | 0,5011 | 0,0147 | S | 0,0065 | S |
| A4 | 0,5092 | 0,0228 | S | 0,0081 | S |
| A5 | 0,5167 | 0,0303 | S | 0,0075 | S |
| A6 | 0,5232 | 0,0368 | S | 0,0066 | S |
| A7 | 0,5296 | 0,0432 | S | 0,0064 | S |
| A8 | 0,5292 | 0,0428 | S | -0,0004 | |
| A9 | 0,5320 | 0,0456 | S | 0,0027 | |
| A10 | 0,5284 | 0,0420 | S | -0,0035 | |
| 1) C = alleen moeder onbekend, A = vaders en moeders onbekend. De getallen duiden de modellen aan. 2) Het verschil is positief en minimaal twee keer zo groot als de bijbehorende standaardfout. | |||||
| Deel-populatie1) | κ0 (gem.) | Δκ0 huidig (gem.) | Signifi-cantie2) | Δκ0 cumulatief (gem.) | Signifi-cantie2) |
|---|---|---|---|---|---|
| B huidig | 0,2350 | ||||
| B1 | 0,2238 | -0,0112 | |||
| B2 | 0,2398 | 0,0048 | S | 0,0160 | |
| B3 | 0,2463 | 0,0114 | S | 0,0066 | |
| B4 | 0,2496 | 0,0146 | S | 0,0032 | |
| B5 | 0,2509 | 0,0159 | S | 0,0013 | |
| B6 | 0,2539 | 0,0189 | S | 0,0030 | |
| B7 | 0,2549 | 0,0200 | S | 0,0010 | |
| B8 | 0,2567 | 0,0218 | S | 0,0018 | |
| B9 | 0,2565 | 0,0215 | S | -0,0002 | |
| B10 | 0,2574 | 0,0224 | S | 0,0009 | |
| A huidig | 0,2132 | ||||
| A1 | 0,1984 | -0,0148 | |||
| A2 | 0,2190 | 0,0057 | S | 0,0205 | |
| A3 | 0,2322 | 0,0189 | S | 0,0132 | |
| A4 | 0,2352 | 0,0220 | S | 0,0031 | |
| A5 | 0,2388 | 0,0256 | S | 0,0036 | |
| A6 | 0,2374 | 0,0242 | S | -0,0014 | |
| A7 | 0,2409 | 0,0276 | S | 0,0035 | |
| A8 | 0,2401 | 0,0269 | S | -0,0008 | |
| A9 | 0,2415 | 0,0282 | S | 0,0014 | |
| A10 | 0,2383 | 0,0251 | S | -0,0031 | |
| 1) B = alleen vader onbekend, A = vaders en moeders onbekend. De getallen duiden de modellen aan. 2) Het verschil is positief en minimaal twee keer zo groot als de bijbehorende standaardfout. | |||||
| Deel-populatie1) | κ1 (gem.) | Δκ1 huidig (gem.) | Signifi-cantie2) | Δκ1 cumulatief (gem.) | Signifi-cantie2) |
|---|---|---|---|---|---|
| B huidig | 0,4948 | ||||
| B1 | 0,4837 | -0,0110 | |||
| B2 | 0,5068 | 0,0121 | S | 0,0231 | S |
| B3 | 0,5116 | 0,0169 | S | 0,0048 | S |
| B4 | 0,5159 | 0,0212 | S | 0,0043 | S |
| B7 | 0,5208 | 0,0261 | S | 0,0011 | S |
| B8 | 0,5229 | 0,0281 | S | 0,0020 | S |
| B9 | 0,5233 | 0,0286 | S | 0,0005 | |
| B10 | 0,5234 | 0,0286 | S | 0,0001 | |
| A huidig | 0,4574 | ||||
| A1 | 0,4410 | -0,0164 | |||
| A2 | 0,4694 | 0,0120 | S | 0,0284 | S |
| A3 | 0,4802 | 0,0229 | S | 0,0109 | S |
| A4 | 0,4884 | 0,0310 | S | 0,0082 | S |
| A5 | 0,4905 | 0,0332 | S | 0,0021 | |
| A6 | 0,4908 | 0,0334 | S | 0,0002 | |
| A7 | 0,4934 | 0,0360 | S | 0,0026 | |
| A8 | 0,4918 | 0,0345 | S | -0,0015 | |
| A9 | 0,4942 | 0,0369 | S | 0,0024 | |
| A10 | 0,4920 | 0,0346 | S | -0,0022 | |
| 1) B = alleen vader onbekend, A = vaders en moeders onbekend. De getallen duiden de modellen aan. 2) Het verschil is positief en minimaal twee keer zo groot als de bijbehorende standaardfout. | |||||
Tabel 3.3.19 toont per model en per deelpopulatie de vertekening en de wortel van de gemiddelde kwadratische afwijking (RMSE) van de onderwijsscores op basis van geïmputeerde opleidingsniveaus. Hierbij is de vertekening gedefinieerd als het gemiddelde verschil tussen de scores op basis van imputaties en op basis van echte waarden, en de RMSE als de standaarddeviatie van dit verschil tussen scores. Een imputatiemodel werkt beter naarmate de vertekening en RMSE dichter bij 0 liggen. Te zien is dat voor alle drie de deelpopulaties de meest complexe modellen leidden tot de kleinste (absolute) vertekening en ook de kleinste RMSE. De uitkomsten voor modellen 7 t/m 10 liggen steeds dicht bij elkaar.
| deelpopulatie | model | vertekening | RMSE |
|---|---|---|---|
| alleen moeder onbekend (C) | huidig | -0,1588 | 2,4113 |
| 1 | -0,3485 | 2,3904 | |
| 2 | -0,3193 | 2,3914 | |
| 3 | -0,3222 | 2,3709 | |
| 4 | -0,1435 | 2,3752 | |
| 5 | -0,1430 | 2,3649 | |
| 6 | -0,1374 | 2,3553 | |
| 7 | -0,1355 | 2,3465 | |
| 8 | -0,1408 | 2,3457 | |
| 9 | -0,1328 | 2,3397 | |
| 10 | -0,1339 | 2,3349 | |
| alleen vader onbekend (B) | huidig | -0,0128 | 1,9888 |
| 1 | 0,0323 | 2,0168 | |
| 2 | 0,0011 | 1,9354 | |
| 3 | 0,0201 | 1,9319 | |
| 4 | -0,0087 | 1,9104 | |
| 5 | -0,0138 | 1,9067 | |
| 6 | -0,0174 | 1,903 | |
| 7 | -0,0226 | 1,8989 | |
| 8 | -0,0143 | 1,8903 | |
| 9 | -0,0154 | 1,8875 | |
| 10 | -0,0170 | 1,8879 | |
| beide onbekend (A) | huidig | -0,3472 | 4,2333 |
| 1 | -0,5954 | 4,285 | |
| 2 | -0,5919 | 4,1013 | |
| 3 | -0,5585 | 4,1229 | |
| 4 | -0,3453 | 4,0584 | |
| 5 | -0,3756 | 3,9713 | |
| 6 | -0,3373 | 3,9398 | |
| 7 | -0,3083 | 3,9218 | |
| 8 | -0,3517 | 3,932 | |
| 9 | -0,3332 | 3,9141 | |
| 10 | -0,3295 | 3,9035 | |
Validatiestudie
Figuren 3.3.20 tot en met 3.3.23 tonen de verschillen tussen de geschatte verdeling van opleidingsniveau voor moeders en vaders op basis van de geïmputeerde waarden en de waargenomen waarden uit 2022 (als proxy voor de echte waarden in 2021). De opbouw van deze figuren is hetzelfde als bij de figuren 3.3.11 tot en met 3.3.14, alleen is de foutenbalk nu gebaseerd op de variantiebenadering uit Bijlage 3.
In vergelijking met de simulatiestudie zijn nu iets grotere afwijkingen te zien. Net als in de simulatiestudie, zijn de uitkomsten van de verschillende imputatiemodellen redelijk vergelijkbaar, in elk geval vanaf het moment dat de leeftijd van de ouder is opgenomen in het model (model 4).
Tabel 3.3.24 en 3.3.25 laten uitkomsten zien over κ0 en κ1, de gerealiseerde fractie imputaties die exact gelijk zijn aan de juiste categorie of daar maximaal één categorie naast zitten, voor moeders (tabel 3.3.24) en vaders (tabel 3.3.25). Bij de meest complexe modellen is een kleine verbetering in κ0 en κ1 te zien ten opzichte van het huidige imputatiemodel. De verschillen tussen de meest complexe modellen onderling zijn echter klein en het meest complexe model scoort niet per se het beste. De ‘beste’ modellen die bij de resultaten van de simulatiestudie zijn voorgesteld als compromis lijken ook op basis van de resultaten in de tabellen 3.3.24 en 3.3.25 een redelijke keuze.
| deelpopulatie | model | ||
|---|---|---|---|
| κ0 | κ1 | ||
| alleen moeder onbekend (C) | huidig | 0,2211 | 0,4923 |
| 1 | 0,2057 | 0,4674 | |
| 2 | 0,2156 | 0,4825 | |
| 3 | 0,2199 | 0,4897 | |
| 4 | 0,2259 | 0,4926 | |
| 5 | 0,2314 | 0,5032 | |
| 6 | 0,2221 | 0,4880 | |
| 7 | 0,2346 | 0,5000 | |
| 8 | 0,2328 | 0,5018 | |
| 9 | 0,2346 | 0,5003 | |
| 10 | 0,2262 | 0,5020 | |
| beide onbekend (A) | huidig | 0,2049 | 0,4719 |
| 1 | 0,1993 | 0,4543 | |
| 2 | 0,2074 | 0,4689 | |
| 3 | 0,2035 | 0,4641 | |
| 4 | 0,2025 | 0,4663 | |
| 5 | 0,2105 | 0,4795 | |
| 6 | 0,2194 | 0,4953 | |
| 7 | 0,2269 | 0,5010 | |
| 8 | 0,2164 | 0,4906 | |
| 9 | 0,2167 | 0,4924 | |
| 10 | 0,2233 | 0,4990 | |
| deelpopulatie | model | ||
|---|---|---|---|
| κ0 | κ1 | ||
| alleen vader onbekend (B) | huidig | 0,2033 | 0,4481 |
| 1 | 0,1920 | 0,4347 | |
| 2 | 0,2052 | 0,4627 | |
| 3 | 0,2049 | 0,4600 | |
| 4 | 0,2149 | 0,4603 | |
| 5 | 0,2152 | 0,4655 | |
| 6 | 0,2163 | 0,4704 | |
| 7 | 0,2273 | 0,4807 | |
| 8 | 0,2249 | 0,4880 | |
| 9 | 0,2195 | 0,4757 | |
| 10 | 0,2191 | 0,4737 | |
| beide onbekend (A) | huidig | 0,1966 | 0,4277 |
| 1 | 0,1823 | 0,4173 | |
| 2 | 0,1862 | 0,4263 | |
| 3 | 0,2050 | 0,4392 | |
| 4 | 0,2110 | 0,4454 | |
| 5 | 0,2069 | 0,4484 | |
| 6 | 0,2141 | 0,4564 | |
| 7 | 0,2164 | 0,4548 | |
| 8 | 0,2096 | 0,4503 | |
| 9 | 0,2102 | 0,4567 | |
| 10 | 0,2146 | 0,4600 | |
Tabel 3.3.26 toont de vertekening en RMSE, op dezelfde manier als eerder in tabel 3.3.19. Ook hier zijn de conclusies hetzelfde als bij de simulatiestudie. De uitkomsten voor modellen 7 t/m 10 liggen steeds dicht bij elkaar.
| deelpopulatie | model | vertekening | RMSE |
|---|---|---|---|
| alleen moeder onbekend (C) | huidig | 0,9061 | 2,6337 |
| 1 | 0,6967 | 2,5924 | |
| 2 | 0,7677 | 2,5953 | |
| 3 | 0,7150 | 2,6246 | |
| 4 | 0,8281 | 2,6388 | |
| 5 | 0,8160 | 2,6106 | |
| 6 | 0,8463 | 2,6036 | |
| 7 | 0,8459 | 2,5987 | |
| 8 | 0,8693 | 2,5791 | |
| 9 | 0,8607 | 2,5856 | |
| 10 | 0,8712 | 2,5944 | |
| alleen vader onbekend (B) | huidig | 0,3824 | 2,1936 |
| 1 | 0,5055 | 2,2453 | |
| 2 | 0,5056 | 2,1810 | |
| 3 | 0,4577 | 2,1933 | |
| 4 | 0,4541 | 2,1978 | |
| 5 | 0,4717 | 2,1961 | |
| 6 | 0,4444 | 2,1752 | |
| 7 | 0,4542 | 2,1910 | |
| 8 | 0,4817 | 2,1846 | |
| 9 | 0,4629 | 2,1830 | |
| 10 | 0,4628 | 2,1879 | |
| beide onbekend (A) | huidig | 0,7178 | 2,8088 |
| 1 | 0,6155 | 2,8126 | |
| 2 | 0,6230 | 2,7719 | |
| 3 | 0,6298 | 2,7838 | |
| 4 | 0,7136 | 2,7951 | |
| 5 | 0,7284 | 2,7566 | |
| 6 | 0,7048 | 2,7127 | |
| 7 | 0,7022 | 2,7226 | |
| 8 | 0,7195 | 2,7217 | |
| 9 | 0,7188 | 2,7299 | |
| 10 | 0,7071 | 2,7115 | |
3.4 Conclusies
Imputatie hulpvariabelen
Voor de imputatie van de achtergrondkenmerken, die uiteindelijk gebruikt zullen worden voor de imputatie van het opleidingsniveau, stellen we een nieuwe methode voor. Ten eerste zullen we de methode versnellen en beter passend maken bij de kenmerken door een random forest model te gebruiken met het mice package. Ten tweede breiden we de kenmerken uit door ook de kenmerken van de andere ouder mee te nemen. Tot slot voegen we ook nog kenmerken toe met betrekking tot het opleidingsniveau van de ouders waar deze wel bekend is. De aanpassingen laten zien dat de imputaties stabieler worden en in totaal een frequentieverdeling hebben voor de kenmerken die aansluit bij de originele dataset met ontbrekende waarden.
Regressiemethodiek opleidingsniveau
De uitkomsten van de analyse hebben laten zien dat de verschillen vallen binnen de ‘normale imputatieruis’ van de bestaande methode. Omdat bij multinomiale logistische regressie minder maatwerk nodig is in de programmatuur en meer gebruik kan worden gemaakt van standaard beschikbare programmatuur is het aan te bevelen om in de toekomst multinomiale logistische regressie te gebruiken voor het imputeren van opleidingsniveaus voor gebruik bij de risico-indicator onderwijsachterstanden.
Imputatie opleidingsniveau
Afgaand op de simulatiestudie en validatiestudie lijken de imputatiemodellen 7 t/m 10 voor moeders en vaders de beste resultaten te geven, waarbij de resultaten voor deze modellen onderling van vergelijkbare kwaliteit zijn. Met name op basis van de conclusies die zijn getrokken uit tabellen 3.3.15 t/m 3.3.18 stellen we voor om de volgende modellen te kiezen:
- Deelpopulatie C (moeders) – model 9:
opleidingsniveau vader [8] × (inkomen moeder [21] + herkomstgroepering moeder [8] + type economische activiteit werkgever moeder [12] + leeftijd moeder [5] + welvaart huishouden [21] + deeltijdfactor werk moeder [11] + sociaaleconomische categorie moeder [13] + stedelijkheidsgraad buurt [6] + burgerlijke staat moeder [4]) - Deelpopulatie B (vaders) – model 8:
opleidingsniveau moeder [8] × (inkomen vader [21] + type economische activiteit werkgever vader [12] + herkomstgroepering vader [8] + leeftijd vader [5] + sociaaleconomische categorie vader [13] + stedelijkheidsgraad buurt [6] + welvaart huishouden [21] + deeltijdfactor werk vader [11]) - Deelpopulatie A (moeders) – model 7:
inkomen moeder [21] × (herkomstgroepering moeder [8] + type economische activiteit werkgever moeder [12] + welvaart huishouden [21] + leeftijd moeder [5] + sociaaleconomische categorie moeder [13] + deeltijdfactor werk moeder [11] + stedelijkheidsgraad buurt [6]) - Deelpopulatie A (vaders):
hetzelfde model als bij deelpopulatie B
(NB: voor vaders in deelpopulatie A is het eerder geïmputeerde opleidingsniveau van de moeder beschikbaar als kenmerk voor het imputatiemodel. Daarom kan voor de vaders in deelpopulatie A hetzelfde imputatiemodel worden gebruikt als in deelpopulatie B).
4. Imputatie onderwijsscores
4.1 Inleiding
Binnen de systematiek van de huidige risico-indicator onderwijsachterstanden kan voor een klein deel van de kinderen geen risico op onderwijsachterstand worden berekend omdat er belangrijke achtergrondgegevens ontbreken. Meestal gaat dit om kinderen van wie we niet beschikken over informatie van één of beide ouders (ongeveer 5 procent van alle peuters van 2,5 tot 4 jaar en alle basisschoolleerlingen). Uit de plausibiliteitsanalyses van de achterstandsscores voor scholen en gemeenten die het CBS jaarlijks publiceert blijkt dat de (geïmputeerde) onderwijsscores van deze leerlingen jaar-op-jaar sterk kunnen fluctueren. Dit kan leiden tot sterke fluctuaties van de achterstandsscores (en dus het toegekende budget) van scholen waarbij voor een groot aandeel van de leerlingen de onderwijsscore wordt geïmputeerd. Het verbeteren van de imputatiemethode van onderwijsscores kan leiden tot kleinere verschillen in onderwijsscores jaar-op-jaar en mogelijk een stabielere toekenning van de verdeling van het onderwijsachterstandenbudget. Voor de herijking van het imputatiemodel onderzoeken we welke additionele achtergrondkenmerken kunnen worden meegenomen om onderwijsscores preciezer te kunnen schatten. Daarnaast onderzoeken we of de imputatiemethode verbeterd kan worden door het model op te splitsen naar subgroepen en te kijken naar verschillende voorspelmethodes om te zorgen voor meer stabiliteit in geïmputeerde scores op individueel niveau, schoolniveau en gemeenteniveau over de tijd.
4.2 Data en methoden
In dit onderzoek maken we gebruik van de data van de risico-indicator onderwijsachterstanden basisonderwijs. Dit bestand bevat de gegevens van alle kinderen van 2,5 tot 4 jaar en basisschoolleerlingen op 1 februari in de jaren 2022 en 2023. Omdat er voor een klein deel van de kinderen geen risico op onderwijsachterstand kan worden berekend, wordt de onderwijsscore geïmputeerd. Welke imputatiemethode wordt gebruikt is afhankelijk van welke informatie er wél beschikbaar is:
- Een kind staat wel ingeschreven in de BRP, maar één of beide ouders niet.
- Een kind staat niet ingeschreven in de BRP.
- Een kind staat geregistreerd als asielzoeker en/of heeft een verblijfsvergunning gekregen.
Voor het verbeteren van de imputatie van onderwijsscores richtten we ons op de grootste groep van de kinderen waarvoor geïmputeerd moet worden: de kinderen die zelf wel staan ingeschreven in de BRP maar van wie één of beide ouders niet bekend zijn in de registers van het CBS.
Met behulp van predictive mean matching wordt er voor deze kinderen een onderwijsscore geïmputeerd. Dit imputatieproces bestaat uit 3 stappen. In de eerste stap wordt er op basis van een groep kinderen voor wie de onderwijsscore direct is bepaald (de donorgroep) een voorspelmodel geschat om onderwijsscores te kunnen voorspellen. In de tweede stap wordt dit voorspelmodel gebruikt om een onderwijsscore te schatten voor zowel de kinderen van wie geen onderwijsscore kon worden berekend (de te imputeren groep) als voor de kinderen uit de donorgroep. In de laatste stap wordt er voor de kinderen uit de te imputeren groep een donor geselecteerd van wie de voorspelde score dichtbij de voorspelde score van te imputeren score ligt. Vervolgens wordt dan de daadwerkelijke score van de donor overgenomen voor het kind uit de te imputeren groep. De uiteindelijke selectie van de donor is iets ingewikkelder en vindt tevens plaats in verschillende stappen; een uitgebreide beschrijving van de imputatiemethode is te vinden in het vierde methodologische rapport van de vorige herijking.
Om de huidige imputatiemethode van onderwijsscores te verbeteren richtten we ons in dit onderzoek op het optimaliseren van het voorspelmodel. De verbetering van het imputatiemodel delen we op in verschillende stappen, zoals weergegeven in figuur 4.2.1.
4.2.1 Stappen in analyse
Gedurende deze stappen willen we de volgende onderzoeksvragen beantwoorden:
- Hoe kunnen we het huidige imputatiemodel opsplitsen naar imputatiecategorie om zo de voorspelling van onderwijsscores te optimaliseren (stap 1)?
- Welke (combinatie van) achtergrondkenmerken kan het best worden gebruikt om met een lineair-regressiemodel de onderwijsscore te schatten (stap 2)?
- In hoeverre resulteert de aangepaste imputatiemethode in meer stabiliteit in onderwijsscores (individueel niveau) en achterstandsscores (schoolniveau en gemeenteniveau) ten opzichte van de huidige imputatiemethode (stap 3)?
Het imputatiemodel schatten we op een subset van de data met peildatum 1 februari 2023 (schooljaar 2022/’23) waarin enkel kinderen voorkomen van wie de onderwijsscore direct is bepaald en het opleidingsniveau van tenminste één van de ouders bekend is. Om de variabele selectie te valideren worden daarnaast de data met peildatum 1 februari 2022 (schooljaar 2021/’22) gebruikt.
Stap 1: Differentiëren imputatiemodel
De eerste stap betreft een meer gedifferentieerde aanpak van de imputatie van onderwijsscores met predictive mean matching. Het huidige voorspelmodel is uniform voor de drie te imputeren categorieën (vader onbekend, moeder onbekend, of beide ouders onbekend). Dit betekent dat een beperkt aantal achtergrondkenmerken kan worden gebruikt om de onderwijsscores te voorspellen, waardoor niet alle relevante informatie kan worden benut voor elke categorie. Deze aanpak kan resulteren in suboptimale voorspellingen van onderwijsscores, omdat het model gedwongen wordt om dezelfde set variabelen te gebruiken voor de drie categorieën, zelfs wanneer er mogelijk meer informatie beschikbaar is. We zouden bijvoorbeeld in de groep waarbij informatie van de moeder ontbreekt gegevens van de vader kunnen gebruiken om onderwijsscores beter te voorspellen. Het opsplitsen van het voorspelmodel voor de drie imputatiecategorieën en het aanpassen van de voorspellende variabelen aan de specifieke imputatiecategorie kan leiden tot meer accurate voorspellingen.
Door het voorspelmodel op te splitsen in drie verschillende modellen, kan er in stap 2 worden gekeken welke achtergrondkenmerken het best meegenomen kunnen worden voor de drie verschillende imputatiecategorieën.
Stap 2: Stepwise regressieanalyse
Om onderwijsscores zo nauwkeurig mogelijk te kunnen schatten wordt er onderzocht welke achtergrondkenmerken van het kind en de ouders het best kunnen worden toegevoegd aan het voorspelmodel. Hierbij wordt in eerste instantie enkel gekeken naar variabelen die al aanwezig zijn in de onderzoeksbestanden van de risico-indicator onderwijsachterstanden. Het huidige voorspelmodel bestaat uit de volgende achtergrondkenmerken:
- Herkomst van het kind;
- Verblijfsduur van moeder (wanneer bekend);
- Huishoudinkomen (inkomen vader + moeder opgeteld, wanneer bekend);
- Ouders wel/niet in schuldhulpverlening;
- Nederlands onderwijs anderstaligen (NOAT).
Dit model willen we iets aanpassen en uitbreiden met een aantal achtergrondkenmerken van het kind en van de ouders (wanneer bekend én beschikbaar in de onderzoeksbestanden). Het NOAT kenmerk wordt niet meer meegenomen omdat dit kenmerk in de nabije toekomst niet meer beschikbaar is.
Kindkenmerken
De achtergrondkenmerken van het kind zijn bekend voor alle kinderen die staan ingeschreven in de BRP en kunnen dus voor alle drie de imputatiecategorieën worden toegevoegd aan het voorspelmodel. De volgende achtergrondkenmerken zullen worden toegevoegd aan de stepwise regressieanalyse:
- Leeftijd kind;
- Leeftijd waarop het kind naar Nederland kwam (leeftijd van het kind minus de verblijfsduur van het kind);
- Stedelijkheid van de buurt waarin het kind woont.
Ouderkenmerken
Voor de twee imputatiecategorieën waarvan tenminste één van beide ouders bekend is kunnen we een aantal achtergrondkenmerken toevoegen van de andere ouder om de onderwijsscore nauwkeuriger te kunnen schatten. De volgende achtergrondkenmerken zullen worden toegevoegd aan de stepwise regressieanalyse:
- Opleidingsniveau vader/moeder;
- Leeftijd vader/moeder;
- Sociaal-economische categorie vader/moeder;
- Burgerlijke staat vader/moeder;
- Inkomen vader/moeder (hiervoor toetsen we juridisch inkomen opgesplitst in 10 en 20 percentielen);
- Verblijfsduur vader/moeder (hiervoor toetsen we zowel een categorische variabele als een continue variabele).
Wat het inkomen van ouders betreft was het initiële plan om inkomen als continue variabele mee te nemen in het voorspelmodel. Op deze manier zou zoveel mogelijk informatie kunnen worden gebruikt om onderwijsscores van leerlingen te voorspellen. Bij het inspecteren van de verschillende variabelen bleek echter dat er voor juridisch inkomen uitzonderlijke uitschieters aanwezig waren. Omdat dit kan resulteren in een schending van assumpties hebben we besloten om de variabele juridisch inkomen aan te passen naar percentielen om zo uitschieters te voorkomen.
Stepwise regressieanalyse
Door het uitvoeren van een stepwise regressieanalyse kunnen de belangrijkste achtergrondkenmerken worden geselecteerd. Met behulp van een forward search wordt gezocht naar het best passende model voor onze data:
- Start met een leeg regressiemodel (bevat enkel een constante term).
- Het regressiemodel wordt stap voor stap opgebouwd door steeds één kenmerk toe te voegen. Bij elke stap wordt het kenmerk geselecteerd dat leidt tot de grootste verbetering in het Bayesiaanse Informatie Criterium (BIC).
- Dit proces wordt herhaald totdat het toevoegen van extra kenmerken niet langer resulteert in een significante verbetering van de BIC-waarde.
Met behulp van deze methode kunnen we een voorspelmodel ontwikkelen voor de drie imputatiecategorieën waarbij er een goede balans is tussen de complexiteit van het model en de nauwkeurigheid van de voorspellingen van onderwijsscores. De resultaten van de forward search geven een bepaalde volgorde van de achtergrondkenmerken, waarbij de kenmerken die het belangrijkst zijn voor het schatten van de onderwijsscores als eerste worden toegevoegd.
Daarnaast voeren we ter vergelijking ook een backward search uit:
- Start met een volledig regressiemodel (bevat alle achtergrondkenmerken).
- Het regressiemodel wordt stap voor stap afgebouwd door steeds één kenmerk weg te laten. Bij elke stap wordt het kenmerk geselecteerd dat leidt tot de grootste verbetering in het Bayesiaanse Informatie Criterium (BIC).
- Dit proces wordt herhaald totdat het verwijderen van kenmerken niet langer resulteert in een significante verbetering van de BIC-waarde.
Tot slot is er onderzocht of de selectie van de achtergrondkenmerken hetzelfde is bij het uitvoeren van een gecombineerde forward en backward search. Hierbij worden beide methodes achter elkaar uitgevoerd, bij een forward-backward search kunnen de toegevoegde kenmerken later weer worden verwijderd, en bij een backward-forward search juist andersom. De stepwise analyses worden in eerste instantie uitgevoerd op de data met peildatum 1 februari 2023, maar worden herhaald op de data met peildatum 1 februari 2022 om te zien in hoeverre de selectie en volgorde van achtergrondkenmerken overeenkomt voor beide peildata.
Definitief voorspelmodel
In het huidige imputatiemodel wordt er een eenvoudig lineair regressiemodel geschat voor de verwachte onderwijsscore. Een lineair regressiemodel kan worden gebruikt om de relatie tussen twee (of in dit geval meerdere) variabelen te onderzoeken en kwantificeren. Het voordeel van een lineair regressiemodel is dat dit eenvoudig te begrijpen is en de coëfficiënten van de achtergrondkenmerken makkelijk te interpreteren zijn. Daarnaast zijn lineaire modellen snel te trainen en werken ze efficiënt voor grote datasets. Een nadeel is echter dat het model lineaire samenhang tussen variabelen veronderstelt, wat beperkend kan zijn voor de nauwkeurigheid van schattingen voor onderwijsscores als de relatie tussen de achtergrondkenmerken en onderwijsscores in de realiteit complexer blijkt te zijn. Daarom is het van belang dat voor geselecteerde achtergrondkenmerken de lineariteit van het verband met de uitkomstvariabele in het voorspelmodel, de onderwijsscore, beoordeeld wordt.
Daarnaast is het van belang dat er wordt gekeken of sommige achtergrondkenmerken mogelijk sterk aan elkaar gerelateerd zijn (multicollineariteit). Dit kan als gevolg hebben dat de effectgroottes per kenmerk niet goed meetbaar zijn. Om te toetsen of er sprake is van multicollineariteit berekenen we de Variance Inflation Factor (VIF) per kenmerk. Een VIF waarde hoger dan 5 wordt vaak als problematisch gezien. Ten slotte toetsen we ook nog de normaliteit en heteroscedasticiteit van de 3 voorspelmodellen.
Stap 3: Evaluatie van nieuwe imputatiemethode
Om de werking van de nieuwe imputatiemethode ten opzichte van de huidige methode te kunnen toetsen zal er worden gekeken of de nieuwe methode zorgt voor meer stabiliteit in geïmputeerde scores over de tijd. Deze toetsing zal plaatsvinden op drie niveaus, namelijk op individueel-, school-, en gemeenteniveau.
Op individueel niveau zullen de verschillen in onderwijsscores van 2023 ten opzichte van 2022 vergeleken worden voor de huidige en de nieuwe imputatiemethode. Er wordt dan gekeken naar de leerlingen van wie de onderwijsscore direct is geïmputeerd omdat A) moeder onbekend is, B) vader onbekend is, en C) beide ouders onbekend zijn. De verwachting is dat door het uitbreiden van het voorspelmodel met name voor groep A en B de onderwijsscores preciezer worden voorspeld en daardoor stabieler over de jaren heen.
Omdat het CBS gebruik maakt van registerdata is het bijvoorbeeld mogelijk dat informatie over de vader van leerling A in 2022 ontbreekt, terwijl in 2023 de vader van leerling A wel staat geregistreerd. Dat betekent dat de onderwijsscore van leerling A in 2022 moest worden geïmputeerd, terwijl in 2023 de onderwijsscore wel berekend kon worden. Van het totaal aantal leerlingen (N = 146979) uit de drie imputatiecategorieën is 33,5% gewisseld tussen de jaren 2022 en 2023. Dit gaat over een wisseling binnen de drie imputatiecategorieën (bijvoorbeeld van beide ouders onbekend naar vader onbekend), of een wisseling van wel of geen imputatie van onderwijsscore. Voor een correcte vergelijking van de huidige en nieuwe imputatiemethodes van onderwijsscores op individueel niveau is het belangrijk om enkel te kijken naar leerlingen die in 2022 en 2023 niet gewisseld zijn van imputatiecategorie (N = 97694).
In lijn met de individuele scores verwachten we ook voor de geaggregeerde achterstandsscores per school meer stabiliteit over de jaren heen. Om dit te onderzoeken zullen de verschillen in achterstandsscores van 2023 ten opzichte van 2022 worden vergeleken voor de huidige en de nieuwe imputatiemethode. Dit wordt gedaan voor alle scholen in Nederland, voor scholen waarvan minstens tien procent van de onderwijsscores direct is geïmputeerd, en scholen waarvan minstens 25 procent van de onderwijsscores direct is geïmputeerd.
Het CBS telt per school de scores op van de leerlingen die landelijk gezien tot de vijftien procent laagst scorende leerlingen behoren: de bruto achterstandsscore. Om versnippering van het budget tegen te gaan wordt er een drempelwaarde in mindering gebracht op deze achterstandsscore: de netto achterstandsscore. Hierdoor ontvangen alleen scholen met een relatief hoge achterstandsscore middelen. De drempelwaarde hangt af van het totaal aantal leerlingen op een school: hoe meer leerlingen, des te hoger de drempelwaarde.
Voor de evaluatie van de imputatiemethode kijken we naar de stabiliteit van achterstandsscores van jaar op jaar. In dat geval is het zinvoller om te kijken naar de verschillen in bruto achterstandsscores, omdat het hanteren van een drempelwaarde deze verschillen licht kan vervormen. Als voorbeeld: school A behaalde in 2022 een bruto achterstandsscore van 850 punten, maar na toepassing van de drempelwaarde werd de netto achterstandsscore 0 vanwege het grote aantal leerlingen. In 2023 steeg de bruto achterstandsscore naar 950 punten. Omdat het aantal leerlingen iets afnam, daalde ook de drempelwaarde, waardoor de netto achterstandsscore voor 2023 op 250 uitkwam. Bij gebruik van de netto achterstandsscore lijkt het verschil tussen de jaren 250 punten te zijn, terwijl het feitelijke verschil in bruto achterstandsscore slechts 150 punten bedraagt.
Echter, voor het ministerie van OCW is het ook informatief om te weten wat de nieuwe imputatiemethode voor gevolgen heeft voor de stabiliteit in uiteindelijke netto-achterstandsscores op basis waarvan de middelen worden verdeeld. Daarom zullen voor de totale populatie scholen in Nederland zowel de bruto als netto achterstandsscores worden vergeleken. Om de meest extreme vertekening van verschilscores van de netto achterstandsscores te beperken worden voor deze analyse enkel scholen meegenomen waarvoor de achterstandsscore in géén van de jaren teruggezet is op 0. In andere woorden, er zijn in deze subset enkel scholen meegenomen die in beide jaren een achterstandsscore boven de drempel hadden en dus middelen ontvingen van het ministerie van OCW. Voor de specifieke subgroepen van scholen waarvan minstens 10% van de onderwijsscores direct is geïmputeerd, en scholen waarvan minstens 25% van de onderwijsscores direct is geïmputeerd zullen enkel de bruto-achterstandsscores worden vergeleken.
De verwachting is dat de spreiding van de verschilscores jaar-op-jaar kleiner zal zijn voor de nieuwe imputatiemethode, en dan met name voor de scholen met veel leerlingen waarvoor de onderwijsscore direct moet worden geïmputeerd. Ten slotte zullen ook de verschillen in bruto en netto achterstandsscores van de gemeenten tussen 2023 en 2022 worden vergeleken. Ook hier wordt meer stabiliteit in achterstandsscores verwacht, wat betekent dat de spreiding van verschilscores voor de nieuwe imputatiemethode kleiner zal zijn dan de huidige imputatiemethode.
4.3 Resultaten
Stap 1: Differentiëren imputatiemodel
Om de onderwijsscores voor de groep kinderen van wie minstens één van beide ouders ontbreekt in de BRP nauwkeuriger te kunnen voorspellen, zoals beschreven in paragraaf 4.1, is het imputatiemodel opgesplitst in drie rondes (voor de drie imputatiecategorieën). De onderwijsscores worden in stappen geïmputeerd: in de eerste ronde voor de kinderen van wie de moeder onbekend is, in de tweede ronde voor de kinderen van wie de vader onbekend is, en in de derde ronde voor de kinderen van wie beide ouders onbekend zijn. Dit betekent dat er drie verschillende voorspelmodellen kunnen worden toegepast, waarbij de meegenomen achtergrondvariabelen afhankelijk zijn van de imputatiecategorie. De achtergrondkenmerken die mogelijk meegenomen kunnen worden zijn weergegeven in tabel 4.3.1. Welke kenmerken daadwerkelijk geselecteerd worden, wordt duidelijk uit de stepwise regressieanalyse. De stepwise regressieanalyse werd uitgevoerd voor model 1 en model 2, waarbij variabelen met achtergrondkenmerken van zowel het kind als de ouders werden geëvalueerd. Voor model 3, waarbij informatie over beide ouders ontbreekt, is geen afzonderlijke analyse uitgevoerd; in plaats daarvan zijn op basis van de resultaten van de stepwise regressieanalyse van model 1 en 2 alleen de beschikbare variabelen (achtergrondkenmerken van het kind) geselecteerd.
| Achtergrondkenmerk | Model 1 | Model 2 | Model 3 | Huidig |
|---|---|---|---|---|
| Moeder onbekend | Vader onbekend | Beide onbekend | ||
| Herkomst kind. | X | X | X | X |
| Huishoudinkomen | X | |||
| Ouders wel/niet in schuldhulpverlening | X | X | X | |
| Leeftijd kind | X | X | X | |
| Leeftijd kind naar Nederland | X | X | X | |
| Stedelijkheid van de buurt | X | X | X | |
| Opleidingsniveau ouder | X | X | X | |
| Leeftijd ouder | X | X | ||
| Sociaal-economische categorie ouder | X | X | ||
| Burgerlijke staat ouder | X | X | ||
| Inkomen ouder (in 10 percentielen) | X | X | ||
| Inkomen ouder (in 20 percentielen) | X | X | ||
| Verblijfsduur ouder (in jaren) | X | X | ||
| Verblijfsduur ouder (categorisch) | X | X | ||
Stap 2: Stepwise regressieanalyse
Na de differentiatie van het huidige imputatiemodel in drie voorspelmodellen en de voorselectie van mogelijke kenmerken is er een stepwise regressieanalyse toegepast. Dit is gedaan om de kenmerken te selecteren die samen de beste voorspelmodellen vormen. Voor zowel model 1 (moeder onbekend) als model 2 (vader onbekend) is er een forward en backward search uitgevoerd en een combinatie van beide. Het doel is om een zo compact mogelijk model over te houden met de belangrijkste achtergrondkenmerken. Voor de verschillende methodes (forward, backward, en combinatie van beide) zijn de modelverbeteringen stapsgewijs vergeleken op basis van de BIC-waarde. De drie methodes leverden elk dezelfde selectie van achtergrondkenmerken voor de individuele voorspelmodellen. Voor het presenteren van de resultaten van de stepwise regressieanalyse zijn de modelkenmerken van de forward selectie als uitgangspunt gebruikt.
Voor de lineaire voorspelmodellen was enkel de volgorde van achtergrondkenmerken van belang bij het selecteren van verschillende vormen van dezelfde variabele, namelijk de variabelen inkomen ouder en verblijfsduur ouder. Voor de variabele inkomen ouder hebben we twee opties toegevoegd, namelijk inkomen in 10 en inkomen in 20 percentielen. Voor verblijfsduur van ouder hebben we ook twee verschillende opties onderzocht, namelijk verblijfsduur ouder in jaren en verblijfsduur ouder in drie categorieën (0-5 jaar, 5-10 jaar en meer dan 10 jaar). Wanneer beide opties voor deze variabelen werden geselecteerd door de stepwise procedure werd enkel de eerst geselecteerde optie gekozen voor het definitieve model.
De volgorde van de geselecteerde kenmerken voor model 1 en model 2 is terug te zien in tabel 4.3.2. De stepwise procedure voor model 1 (moeder onbekend) stopte na de selectie van het twaalfde kenmerk, omdat er volgens het model geen extra verklaringskracht werd toegevoegd. De stepwise procedure voor model 2 (vader onbekend) selecteerde alle toegevoegde kenmerken. Voor zowel model 1 als model 2 werd van inkomen ouder de variabele in 20 percentielen als eerste geselecteerd. Met betrekking tot verblijfsduur werd de categorische variabele als eerste gekozen.
| Volgorde | Model 1 (moeder ontbreekt) | Model 2 (vader ontbreekt) |
|---|---|---|
| 1 | Opleidingsniveau vader | Opleidingsniveau moeder |
| 2 | Herkomst kind | Herkomst kind |
| 3 | Ouders wel/niet in schuldsanering | Verblijfsduur moeder (categorisch) |
| 4 | Inkomen vader (in 20 percentielen) | Leeftijd moeder |
| 5 | Verblijfsduur vader (categorisch) | Ouders wel/niet in schuldsanering |
| 6 | Leeftijd vader | Inkomen moeder (in 20 percentielen) |
| 7 | Leeftijd kind | Burgerlijke staat moeder |
| 8 | Sociaal economische categorie vader | Leeftijd kind |
| 9 | Burgerlijke staat vader | Sociaal economische categorie moeder |
| 10 | Leeftijd kind naar Nederland | Stedelijkheid van de buurt |
| 11 | Verblijfsduur vader (in jaren) | Verblijfsduur moeder (in jaren) |
| 12 | Stedelijkheid van de buurt | Leeftijd kind |
| 13 | - | Inkomen moeder (in 10 percentielen) |
Bovenstaande stepwise regressieanalyse is uitgevoerd op data met peildatum 1 februari 2023. Om de stabiliteit van de twee voorspelmodellen te onderzoeken is de forward stepwise procedure tevens toegepast op data van een jaar eerder, namelijk peildatum 1 februari 2022. De selectie en volgorde van de achtergrondkenmerken van model 1 kwamen voor beide jaren exact overeen. Voor model 2 was er een klein verschil, kenmerk 4 en 5 zijn omgedraaid, en de tweede optie van de variabele inkomen ouder (in 10 percentielen) werd niet geselecteerd, zie tabel 4.3.3.
| Volgorde | Data 2023 | Data 2022 |
|---|---|---|
| 1 | Opleidingsniveau moeder | Opleidingsniveau moeder |
| 2 | Herkomst kind | Herkomst kind |
| 3 | Verblijfsduur moeder (categorisch) | Verblijfsduur moeder (categorisch) |
| 4 | Leeftijd moeder | Ouders wel/niet in schuldsanering |
| 5 | Ouders wel/niet in schuldsanering | Leeftijd moeder |
| 6 | Inkomen moeder (in 20 percentielen) | Inkomen moeder (in 20 percentielen) |
| 7 | Burgerlijke staat moeder | Burgerlijke staat moeder |
| 8 | Leeftijd kind | Leeftijd kind |
| 9 | Sociaal economische categorie moeder | Sociaal economische categorie moeder |
| 10 | Stedelijkheid van de buurt | Stedelijkheid van de buurt |
| 11 | Verblijfsduur moeder (in jaren) | Verblijfsduur moeder (in jaren) |
| 12 | Leeftijd kind naar Nederland | Leeftijd kind naar Nederland |
| 13 | Inkomen moeder (in 10 percentielen) | |
De conclusies van de selectie van achtergrondkenmerken zijn daarom onveranderd en resulteren in de volgende selectie van kenmerken voor model 1 en 2 (waarbij één van de ouders ontbreekt):
- Opleidingsniveau ouder;
- Herkomst kind;
- Ouders wel/niet in schuldsanering;
- Inkomen ouder (in 20 percentielen);
- Verblijfsduur ouder (categorisch);
- Leeftijd ouder;
- Leeftijd kind;
- Sociaal economische categorie ouder;
- Burgerlijke staat ouder;
- Leeftijd kind naar Nederland;
- Verblijfsduur ouder (in jaren);
- Stedelijkheid van de buurt.
Voor model 3, waarbij beide ouders ontbreken, ontbreekt voor een groot aantal van bovenstaande achtergrondkenmerken informatie. Voor dit voorspelmodel blijft een selectie van de volgende achtergrondkenmerken over:
- Herkomst kind;
- Leeftijd kind;
- Leeftijd kind naar Nederland;
- Stedelijkheid van de buurt.
De forward stepwise procedure voegt telkens één achtergrondkenmerk toe aan het voorspelmodel. Bij elke stap wordt het kenmerk geselecteerd dat leidt tot de grootste verbetering in BIC, waarbij een lagere BIC-waarde een betere modelkwaliteit betekent, zie figuur 4.3.4. In de figuur is te zien dat hoe meer kenmerken er worden opgenomen in het model, hoe lager de BIC waarde is en des te beter het voorspelmodel de onderwijsscore van een leerling kan schatten. De BIC neemt voor zowel model 1 als 2 het sterkst af na het toevoegen van het opleidingsniveau van de ouder. Ook na het toevoegen van het tweede achtergrondkenmerk, herkomst van het kind, neemt de BIC nog zichtbaar sterk af. Voor beide modellen geldt dat het toevoegen van het twaalfde kenmerk nog steeds voor een sterke daling zorgt (model 1: -784 en model 2: -378). In model twee wordt inkomen van de moeder (in 10 percentielen) als laatste kenmerk toegevoegd, maar de modelkwaliteit neemt hierbij nog nauwelijks toe (BIC daalt met 43 punten).
| volgorde | model 1 (moeder ontbreekt) | model 2 (vader ontbreekt) |
|---|---|---|
| 0 | 3637799 | 3637799 |
| 1 | 1915803,27978208 | 1351978,44276075 |
| 2 | 1720466,27562503 | 1086213,34839467 |
| 3 | 1706568,47282024 | 1041289,9739666 |
| 4 | 1697811,37628042 | 1021854,68892776 |
| 5 | 1689032,97622276 | 1005033,71876224 |
| 6 | 1681947,0423644 | 993072,832140157 |
| 7 | 1672259,74713793 | 985406,199646535 |
| 8 | 1668851,68033408 | 981481,622260564 |
| 9 | 1665978,20559002 | 977887,16636602 |
| 10 | 1664386,56335636 | 974930,624557848 |
| 11 | 1663446,04919983 | 973733,159121658 |
| 12 | 1662662,10260982 | 973355,23274757 |
| 13 | NA | 973312,586739611 |
Om de betrouwbaarheid van de lineaire regressie voor bovenstaand model te controleren zijn er controles gedaan op een aantal assumpties, waaronder:
- Lineariteit
- Normaliteit
- Heteroscedasticiteit
- Multicollineariteit
- Uitschieters
De assumpties worden gecontroleerd zodat we betrouwbare parameterschattingen krijgen en de resultaten te generaliseren zijn naar de populatie. De assumpties van lineariteit, normaliteit en heteroscedasticiteit zijn visueel gecontroleerd, de multicollineariteit is beoordeeld aan de hand van de Variance Inflation Factor (VIF), en uitschieters zijn visueel geïnspecteerd aan de hand van Cook’s D maat.
In de controles zagen we een schending van de assumpties lineariteit, normaliteit en heteroscedasticiteit, specifiek voor het model waar beide ouders ontbreken. Dit model is beperkter in omvang vanwege minder beschikbare voorspellers door het ontbreken van beide ouders. Dit kan resulteren in meer variatie in de residuen (het verschil tussen de werkelijke en voorspelde score). Omdat we in dit onderzoek met een grote dataset werken en vooral kijken naar de regressiecoëfficiënten en niet direct naar de significantiewaarden van de resultaten, zal de schending van deze assumpties waarschijnlijk niet direct invloed hebben op de interpretatie van de resultaten. Voor de overige twee modellen, waarbij enkel vader of moeder ontbreekt, wees de visuele inspectie niet op een schending van assumpties van lineariteit, normaliteit of heteroscedasticiteit. Ook de controles op multicollineariteit wezen niet op collineariteit in ons voorspelmodel. Doorgaans worden de volgende rule-of-thumb grenswaarden gebruikt: VIF > 20 onbruikbaar, > 10 hoge mate van collineariteit, > 5 enige mate van collineariteit. De VIF-waarden waren voor alle drie de modellen kleiner dan 3. In de subset die gebruik werd voor het schatten van het lineaire voorspelmodel zijn twee records met een onwaarschijnlijk hoge leeftijd (35 en 32 jaar) geëxcludeerd. Deze leeftijden wijzen mogelijk op een registratiefout en zijn om vertekeningen in het voorspelmodel te voorkomen verwijderd voor onze analyses.
| 2023 | 2022 | ||||||
|---|---|---|---|---|---|---|---|
| Model | R2 | MSE | RMSE | R2 | MSE | RMSE | |
| 1: Moeder ontbreekt | 0,74 | 3,15 | 1,77 | 0,74 | 3,16 | 1,78 | |
| 2: Vader ontbreekt | 0,84 | 1,96 | 1,40 | 0,84 | 1,96 | 1,40 | |
| 3: Beide ouders ontbreken | 0,12 | 10,79 | 3,29 | 0,12 | 10,85 | 3,29 | |
Na de selectie van variabelen in de stepwise regressieanalyse en het beoordelen van de assumpties zijn de fitindices van de drie afzonderlijke voorspelmodellen bepaald, zie tabel 4.3.5. De verklaarde variantie (R2) van voorspelmodel 1 en 2 zijn redelijk hoog, waarbij de hogere R2 van model 2 (vader ontbreekt) er op lijkt te wijzen dat de achtergrondkenmerken van moeder de variabiliteit iets sterker lijken te voorspellen in model 2 dan de achtergrondkenmerken van vader in model 1. Echter zijn de verschillen tussen deze modellen niet getoetst, waardoor er geen uitspraken gedaan kunnen worden over of deze verschillen daadwerkelijk statistisch significant zijn. Model 3, waarbij informatie over beide ouders ontbreekt, presteert een stuk minder goed dan de modellen waarbij informatie van één van beide ouders wordt gebruikt. Dit is terug te zien in de lagere verklaarde variantie (R2) en hogere gemiddelde standaardfouten (MSE en RMSE). Het gebruik van beschikbare achtergrondkenmerken van ouders zorgt dus voor meer nauwkeurige voorspellingen van onderwijsscores voor de groepen leerlingen waar één van beide ouders ontbreekt.
Stap 3: Evaluatie van nieuwe imputatiemethode
De werking van de nieuwe imputatiemethode ten opzichte van de huidige imputatiemethode is geëvalueerd aan de hand van de stabiliteit van onderwijsscores en achterstandsscores jaar-op-jaar. Verwacht werd dat de nieuwe uitgebreide voorspelmodellen zorgen voor meer stabiliteit in scores over de jaren heen voor zowel individuele onderwijsscores, achterstandsscores van scholen, en achterstandsscores van gemeenten.
Verschillen in individuele onderwijsscores
Zoals besproken in paragraaf 4.1 zijn enkel de onderwijsscores van kinderen vergeleken die in de jaren 2022 en 2023 niet zijn gewisseld van imputatiecategorie. De verdeling van de verschillen in onderwijsscores van 2023 ten opzichte van 2022 berekend aan de hand van zowel de huidige als de nieuwe imputatiemethode is weergegeven met behulp van een dichtheidsplot, zie figuur 4.3.6. Voor de imputatiegroepen vader onbekend en moeder onbekend is te zien dat bij de nieuwe imputatiemethode de verdeling van de dichtheid van verschilscores iets smaller is. Dit impliceert dat de verschilscores bij gebruik van de nieuwe imputatiemethode minder variabiliteit vertonen jaar-op-jaar, wat kan betekenen dat de nieuwe methode voor meer stabiliteit in geïmputeerde onderwijsscores jaar-op-jaar. Bovendien is te zien dat de piek van de verdeling voor de nieuwe methode met name voor de groep vader onbekend, en in iets mindere mate voor de groepen moeder onbekend en beide ouders onbekend, hoger is dan de piek voor de huidige methode. Dit suggereert dat de gemiddelde verschilscore bij de nieuwe methode dichter bij 0 ligt in vergelijking tot de gemiddelde verschilscore van de huidige methode. Kortom, de nieuwe imputatiemethode lijkt met name voor de groepen vader onbekend en moeder onbekend te zorgen voor minder extreme verschillen tussen geïmputeerde scores jaar-op-jaar. Voor de groep beide ouders onbekend lijkt de nieuwe methode niet voor veel meer stabiliteit in scores jaar-op-jaar te zorgen. Dit is niet geheel onverwacht, aangezien dit voorspelmodel het minst is uitgebreid ten opzichte van de voorspelmodellen voor vader/moeder onbekend.
Het uitbreiden van de voorspelmodellen leidt in de groepen waar één van de ouders ontbreekt inderdaad tot een kleinere variantie in verschilscores. In tabel 4.3.7 zijn de eigenschappen van de verdeling van verschillen tussen onderwijsscores van 2023 en 2022 samengevat voor de huidige en nieuwe imputatiemethode. Voor de groepen uit model 1 en 2 zien we dat de nieuwe methode zorgt voor een kleinere range van verschilscores; de minimum en maximum verschilscores liggen namelijk dichter bij elkaar. Ook de standaarddeviatie daalt voor deze twee groepen, voor de groep moeder ontbreekt daalt deze met 1,61 punt, en voor de groep vader ontbreekt met 0.89 punt. Echter, voor de groep waarbij beide ouders ontbreken treedt er geen verbetering op; de minimum en maximum verschilscores liggen zelfs iets verder uit elkaar en de standaarddeviatie stijgt met 0,34 punt.
| Huidige methode | Nieuwe methode | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | Min | Gemiddelde | Max | SD | Min | Gemiddelde | Max | SD | |
| 1: Moeder ontbreekt | -12,63 | 0,02 | 13,66 | 3,88 | -11,74 | 0,04 | 12,07 | 2,27 | |
| 2: Vader ontbreekt | -12,25 | 0,05 | 12,29 | 3,93 | -11,23 | 0,08 | 11,57 | 3,04 | |
| 3: Beide ouders ontbreken | -13,35 | -0,15 | 12,95 | 4,24 | -13,46 | 0,33 | 14,53 | 4,58 | |
Verschillen in achterstandsscores van scholen
Om te onderzoeken of de nieuwe methode ook zorgt voor meer stabiliteit in achterstandsscores van scholen over de jaren heen zijn de achterstandsscores van 2023 ten opzichte van 2022 vergeleken voor de huidige en nieuwe imputatiemethode. Dit is gedaan voor alle scholen binnen het primair basisonderwijs (met en zonder toepassing van de drempelwaarde), een subset van scholen waarvan minstens 10% van de onderwijsscores direct is geïmputeerd, en een subset van scholen waarvan minstens 25% van de onderwijsscores direct is geïmputeerd.
In tabel 4.3.8 zijn de kenmerken van de verschillen in bruto achterstandsscores (zonder drempel) voor scholen van 2023 ten opzichte van 2022 samengevat. Wanneer we de huidige en nieuwe methode vergelijken zien we een verschuiving van de ondergrens en bovengrens waarbij de range in verschilscores iets kleiner is geworden. Voor de nieuwe methode geldt dat de ondergrens van de verschilscores iets extremer werd, wat betekent dat één of meerdere scholen iets sterker dalen in achterstandsscores. Daarentegen werd de bovengrens van de verschilscores minder extreem, wat impliceert dat met gebruik van de nieuwe methode de meest stijgende school (of scholen) minder stegen in achterstandsscores. Het gemiddelde verschil in achterstandsscores is minimaal. De standaarddeviatie van de verschilscores is bij de nieuwe methode iets lager vergeleken met de huidige methode.
| Model | Aantal scholen | Ondergrens | Gemiddelde verschil | Bovengrens | Standaard Deviatie |
|---|---|---|---|---|---|
| Huidige methode | 6 220 | -327,27 | 0,84 | 626,64 | 46,70 |
| Nieuwe methode | 6 220 | -356,29 | 1,33 | 541,67 | 41,83 |
Wanneer de netto achterstandsscores voor scholen van 2023 ten opzichte van 2022 worden vergeleken is een vergelijkbaar patroon te zien, zie tabel 4.3.9. Voor deze analyse zijn enkel scholen meegenomen die in beide jaren een achterstandsscore boven de drempel hadden om grote vertekening in verschilscores ten gevolge van het toepassen van drempelwaarde te voorkomen. Het gemiddelde verschil in achterstandsscores stijgt voor deze scholen, maar in vergelijking met de huidige methode is dit wederom een minimale stijging. De standaarddeviatie van de verschilscores is bij de nieuwe methode wederom lager. Wel is te zien dat de ondergrens en bovengrens van de verschillen in netto achterstandsscores iets anders verschuiven dan bij het vergelijken van de verschillen in bruto achterstandsscores. Zowel de ondergrens als de bovengrens van de verschilscores met de nieuwe methode zijn iets extremer geworden ten opzichte van de huidige methode. Over het algemeen kan er geconcludeerd worden dat het toepassen van de nieuwe methode zorgt voor iets minder variatie in netto achterstandsscores voor scholen jaar-op-jaar.
| Model | Aantal scholen | Ondergrens | Gemiddelde verschil | Bovengrens | Standaard Deviatie |
|---|---|---|---|---|---|
| Huidige methode | 2 416 | -261,07 | -0,05 | 462,34 | 55,98 |
| Nieuwe methode | 2 434 | -353,13 | 0,09 | 482,51 | 49,53 |
De aanpassingen van de imputatiemethode hebben enkel invloed op de onderwijsscores van leerlingen waarvoor er direct moest worden geïmputeerd, en dan specifiek enkel voor de groep kinderen die zelf wel staan ingeschreven in de BRP maar van wie één of beide ouders niet bekend zijn in de registers van het CBS. Om de huidige en nieuwe imputatiemethode goed te vergelijken zijn daarom de verschillen in achterstandsscores voor scholen waarvan minstens 10% en minstens 25% van de onderwijsscores is geïmputeerd samengevat in tabel 4.3.10 en tabel 4.3.11. Voor deze subsets geldt dat de geselecteerde scholen in beide jaren minstens 10% of minstens 25% van de onderwijsscores moet zijn geïmputeerd.
Voorgaande jaren werd ongeveer zeven procent van de onderwijsscores geïmputeerd. In 2023 is dit iets toegenomen naar ongeveer acht procent van de onderwijsscores. Dit heeft onder andere te maken met een verschuiving van peildata van registerbestanden die nodig zijn om de koppeling te kunnen maken tussen de leerling en de ouder . Dit heeft tot gevolg dat er grotere verschillen dan gebruikelijk zijn in het aandeel directe imputaties van onderwijsscores op scholen. Om verschillen in het aantal directe imputaties van onderwijsscores jaar-op-jaar zo constant mogelijk te houden voor de vergelijking van de huidige en nieuwe imputatiemethode is er daarom nog een extra subset onderzocht. Voor deze subset zijn enkel scholen geselecteerd die maximaal vijf procent verschillen in het aantal directe imputaties van onderwijsscores in 2022 en 2023.
| Model | Aantal scholen | Ondergrens | Gemiddelde verschil | Bovengrens | Standaard Deviatie |
|---|---|---|---|---|---|
| Totaal | |||||
| Huidige methode | 1 246 | -261,07 | 1,39 | 462,34 | 68,23 |
| Nieuwe methode | 1 246 | -353,13 | -0,24 | 482,51 | 59,67 |
| Subset < 5% verschil | |||||
| Huidige methode | 1 009 | -261,07 | -7,21 | 462,34 | 57,46 |
| Nieuwe methode | 1 009 | -353,13 | -4,11 | 332,50 | 53,29 |
| Model | Aantal scholen | Ondergrens | Gemiddelde verschil | Bovengrens | Standaard Deviatie |
|---|---|---|---|---|---|
| Totaal | |||||
| Huidige methode | 267 | -261,07 | 16,61 | 462,34 | 100,66 |
| Nieuwe methode | 267 | -282,65 | 1,52 | 482,51 | 89,45 |
| Subset < 5% verschil | |||||
| Huidige methode | 169 | -261,07 | 0,19 | 462,34 | 87,21 |
| Nieuwe methode | 169 | -230,40 | -7,52 | 332,50 | 80,01 |
Voor scholen waarbij een hoog aandeel van de onderwijsscores direct wordt geïmputeerd lijkt de nieuwe imputatiemethode voor meer stabiliteit in achterstandsscores over de jaren heen te zorgen. Voor deze scholen is het gemiddelde verschil in achterstandsscores tussen 2023 en 2022 ongeveer gehalveerd. Daarnaast is ook de standaarddeviatie van de verschilscores gedaald voor zowel scholen met minstens 10% direct geïmputeerde onderwijsscores als voor scholen met minstens 25% direct geïmputeerde onderwijsscores. Wanneer er enkel gekeken wordt naar de subsets van scholen die in 2022 en 2023 maximaal 5% verschillen in het aandeel directe imputaties is de daling van de standaarddeviatie iets kleiner.
Verschillen in achterstandsscores van gemeenten
Er is ook gekeken of de achterstandsscores van de gemeenten over de jaren heen stabieler werden bij het toepassen van de nieuwe imputatiemethode. Hiervoor zijn de verschillen in netto en bruto achterstandsscores van de gemeenten tussen 2023 en 2022 vergeleken, zie tabel 4.3.12.
| Model | Aantal gemeenten | Ondergrens | Gemiddelde verschil | Bovengrens | Standaard Deviatie |
|---|---|---|---|---|---|
| Huidige methode | 342 | -3284,33 | 1,98 | 986,42 | 305,56 |
| Nieuwe methode | 342 | -2639,80 | 7,95 | 570,10 | 248,54 |
| Model | Aantal gemeenten | Ondergrens | Gemiddelde verschil | Bovengrens | Standaard Deviatie |
|---|---|---|---|---|---|
| Huidige methode | 342 | -3 017 | 5 | 1 070 | 301 |
| Nieuwe methode | 342 | -2 639 | 14 | 564 | 241 |
Vergeleken met de huidige methode is de range tussen de ondergrens en bovengrens van de verschilscores kleiner geworden bij gebruik van de nieuwe methode, dit geldt voor zowel de netto achterstandsscores (met drempel) als de bruto achterstandsscores (zonder drempel). Ook is de standaarddeviatie van de verschilscores bij gebruik van de nieuwe methode gedaald ten opzichte van de huidige methode. Opvallend is dat het gemiddelde verschil juist iets is gestegen, maar deze stijging is relatief klein ten opzichte van de standaarddeviatie. Wanneer de verdeling van de verschilscores voor beide methodes wordt gevisualiseerd, is te zien dat deze stijging in gemiddelde verschilscore waarschijnlijk het resultaat is van het verdwijnen van twee sterke, negatieve, uitschieters bij het toepassen van de nieuwe methode ten opzichte van de huidige methode (zie figuur 4.3.14).
4.4 Conclusies
Dit hoofdstuk betreft de resultaten van de optimalisatie van het voorspelmodel dat gebruikt wordt voor het direct imputeren van onderwijsscores voor leerlingen voor wie er geen onderwijsscore kan worden berekend. Dit onderzoek richt zich op de grootste groep kinderen voor wie de onderwijsscore geïmputeerd moet worden: de kinderen die zelf wel staan ingeschreven in de BRP maar van wie één of beide ouders niet bekend zijn in de BRP. In de eerste stap werd onderzocht of het huidige imputatiemodel opgesplitst kon worden om zo het voorspelmodel voor elke specifieke imputatiegroep te kunnen optimaliseren. Door het voorspelmodel op te splitsen in drie voorspelmodellen voor de drie te imputeren categorieën (vader onbekend, moeder onbekend, en beide ouders onbekend) kunnen er meer achtergrondkenmerken worden meegenomen, wat mogelijk leidt tot meer accurate voorspellingen.
Voor de tweede stap is er voor deze drie imputatiecategorieën onderzocht welke combinatie van achtergrondkenmerken het best gebruikt kan worden om onderwijsscores voor individuele leerlingen te voorspellen. Op basis van de variabelen die al aanwezig zijn in de onderzoeksbestanden van de risico-indicator onderwijsachterstanden is er een lijst met mogelijke verklarende variabelen van onderwijsscores opgesteld. Met behulp van een stepwise-selectie procedure is er onderzocht welke variabelen voldoende verklaringskracht toevoegen om het voorspelmodel te verbeteren. Deze analyses resulteren in de volgende selectie van achtergrondkenmerken voor de groepen leerlingen waarbij één van de ouders ontbreekt:
- Opleidingsniveau ouder
- Ouders wel/niet in schuldsanering
- Inkomen ouder (in 20 percentielen)
- Verblijfsduur ouder (categorisch)
- Leeftijd ouder
- Sociaal economische categorie ouder
- Burgerlijke staat ouder
- Verblijfsduur ouder (in jaren)
- Herkomst kind
- Leeftijd kind
- Leeftijd kind naar Nederland
- Stedelijkheid van de buurt
Voor de leerlingen van wie beide ouders onbekend zijn blijven enkel de laatste vier schuingedrukte achtergrondkenmerken over.
Om de stabiliteit van de selectie van kenmerken voor de voorspelmodellen te onderzoeken is de stepwise-selectie procedure tevens toegepast op data van een eerder cohort. In beide procedures werden dezelfde achtergrondkenmerken geselecteerd, wat de stabiliteit van de selectie van variabelen voor het voorspelmodel lijkt te bevestigen.
In de derde stap is er onderzocht in hoeverre de aangepaste imputatiemethode daadwerkelijk resulteert in meer stabiliteit in onderwijsscores op individueel niveau en achterstandsscores op school- en gemeenteniveau. De nieuwe imputatiemethode zorgt op individueel niveau met name bij de imputatiegroepen ‘vader onbekend’ en ‘moeder onbekend’ voor meer stabiliteit in geïmputeerde onderwijsscores jaar-op-jaar. Voor de groep leerlingen van wie beide ouders onbekend zijn is er geen verbetering te zien wat betreft de stabiliteit in onderwijsscores. Dit is niet verrassend, aangezien het voorspelmodel voor deze groep niet is uitgebreid ten opzichte van de huidige imputatiemethode.
Op schoolniveau is de stabiliteit in achterstandsscores over de jaren heen onderzocht door verschillen in achterstandsscores van 2023 ten opzichte van 2022 te vergelijken voor de huidige en de nieuwe imputatiemethode. Dit is gedaan voor de totale populatie van scholen binnen het primair basisonderwijs, maar ook voor subsets van scholen met een hoog percentage leerlingen voor wie de onderwijsscore direct moest worden geïmputeerd. Voor elke (sub)populatie van scholen is te zien dat de standaarddeviatie van de verschilscores jaar-op-jaar bij gebruik van de nieuwe imputatiemethode lager ligt vergeleken met de huidige methode. De daling in standaarddeviatie van de nieuwe methode ten opzichte van de oude methode varieert, afhankelijk van de specifieke (sub)populatie waar naar gekeken wordt. De daling in de standaarddeviatie lijkt er op te wijzen dat de nieuwe imputatiemethode zorgt voor meer stabiliteit in achterstandsscores, met name voor scholen waar een hoog aandeel van de onderwijsscores van leerlingen moet worden geïmputeerd. Veranderingen in de range en het gemiddelde van de verschilscores waren minder uniform over de verschillende subgroepen heen.
Wanneer er wordt gekeken naar de verschilscores in achterstandsscores voor gemeenten is wederom een verbetering te zien wat betreft de stabiliteit in achterstandsscores. Voor zowel de bruto als netto achterstandsscores zien we dat de range in verschilscores kleiner is geworden. De nieuwe imputatiemethode lijkt ervoor te zorgen dat gemeente-achterstandsscores jaar-op-jaar minder extreem verschillen. Verder impliceert met name de sterke daling van de standaarddeviatie voor zowel de netto als de bruto achterstandsscores dat de nieuwe methode ook voor gemeenten zorgt voor meer stabiliteit in achterstandsscores over de jaren heen.
Tot slot geven we een korte vooruitblik op de tweede fase van dit onderzoekstraject. In deze fase zal de risico-indicator onderwijsachterstanden grootschalig worden herijkt. Ook specifiek voor het direct imputeren van onderwijsscores zal er onderzocht worden hoe de nieuwe methode gepresenteerd in het huidige rapport nog verder kan worden ontwikkeld en verbeterd. Ten eerste zal er worden onderzocht in hoeverre het voorspelmodel nog verder kan worden uitgebreid met achtergrondkenmerken, en dan met name de kenmerken die zijn behandeld in hoofdstuk 3 voor het imputeren van het opleidingsniveau van ouders. Bovendien zal er onderzocht worden of er interacties tussen verschillende kenmerken moeten worden meegenomen in het voorspelmodel. Verder is het voor de volgende fase belangrijk om naar achtergrondkenmerken te kijken die beschikbaar zijn voor de groep leerlingen bij wie informatie over beide ouders ontbreekt, zoals buurtkenmerken. Tevens zullen er alternatieven worden onderzocht voor het imputeren van onderwijsscores van gevallen waar individuele voorspellingen lastig zijn vanwege een gebrek aan achtergrondinformatie. Ook kan er worden gekeken of aanpassingen in de donorselectie voor Predictive Mean Matching kunnen leiden tot verbeteringen in de nauwkeurigheid van imputaties.
Daarnaast kan het verkennen van andere voorspel- en imputatiemethodes, zoals beslisbomen, nieuwe inzichten bieden op het verbeteren van imputaties van onderwijsscores.
Tot slot kan het gebruik van een simulatiestudie waarbij onderwijsscores worden voorspeld voor leerlingen van wie deze berekend kan worden een waardevolle aanvulling zijn, omdat dan niet alleen de stabiliteit van onderwijsscores jaar-op-jaar wordt beoordeeld, maar ook de nauwkeurigheid van de voorspellingen en imputaties van verschillende methodes vergeleken kan worden.
5. Uniformering eindtoetsscores
5.1 Inleiding
Bij de oorspronkelijke ontwikkeling van de risico-indicator onderwijsachterstanden is gekeken – gegeven een bepaalde intelligentie – welke sociaaleconomische achtergrondkenmerken van kinderen een nadelige invloed hebben op de onderwijsprestaties. Omdat destijds het aandeel van de centrale eindtoets van Cito nog op ongeveer 85 procent lag, is er voor gekozen om alleen de kinderen die aan de toets van Cito hadden deelgenomen mee te nemen in de ontwikkeling van het model. Inmiddels is het aandeel van de centrale eindtoets van Cito fors afgenomen en kunnen scholen die een andere eindtoets gebruiken niet worden genegeerd om een aantal redenen. Zo kan het uitsluiten van deze scholen leiden tot selectiebias en het leidt hoe dan ook tot een aanzienlijke beperking van de onderzoekspopulatie.
Voor het onderzoek voor de herijking van het model voor de risico-indicator onderwijsachterstanden is het wenselijk om gebruik te kunnen maken van een uniforme maatstaf voor onderwijsprestaties. Het probleem is echter dat iedere eindtoetsaanbieder een eigen schaal voor de eindtoetsscore hanteert. Omdat het CBS alleen de eindtoetsscores heeft en er geen extra informatie beschikbaar is over hoe de verschillende schalen tot stand zijn gekomen, werken we in dit hoofdstuk verschillende methoden uit om de eindtoetsscores te uniformeren.
5.2 Data en methoden
Voor het toepassen van de verschillende methoden voor uniformering maken we gebruik van een dataset met de populatie leerlingen die in 2021 een eindtoets hebben gemaakt. Daarbij zijn er vijf soorten eindtoetsen: AMN, CET, Dia, Iep en Route 8. Per eindtoetsaanbieder wordt er jaarlijks door de Expertgroep Toetsen PO bepaald wat het bereik aan eindtoetsscores is behorende tot een bepaald toetsadvies, met de volgende mogelijke toetsadviezen: pro/vmbo-b, vmbo-b/k, vmbo-k/gt, vmbo-gt/havo, havo/vwo en vwo. Deze gegevens ontvangt het CBS jaarlijks van DUO met de nieuwe indeling. Hierbij moet opgemerkt worden dat het bereik van de toetsscores behorende tot een toetsadvies verschilt tussen de toetsaanbieders. Daarnaast is de lengte van het bereik van de toetsscores behorende tot een toetsaanbieder verschillend per toetsadvies. In tabel 5.2.1 wordt per toetsaanbieder weergegeven welke eindtoetsscore bij welk toetsadvies hoort, voor de eindtoetsen in 2021.
| Toetsadvies | CET | Route 8 | Iep | Dia | AMN |
|---|---|---|---|---|---|
| Pro / vmbo bl | 501-510 | 100-112 | 50-51 | 321-338 | 300-304 |
| Vmbo bl/kl | 511-523 | 113-159 | 52-68 | 339-349 | 305-332 |
| Vmbo kl/gtl | 524-531 | 160-187 | 69-76 | 350-356 | 333-374 |
| Vmbo gtl/havo | 532-539 | 188-216 | 77-84 | 357-365 | 375-433 |
| Havo/vwo | 540-544 | 217-238 | 85-91 | 366-371 | 434-468 |
| Vwo | 545-550 | 239-300 | 92-100 | 372-390 | 469-500 |
Gegeven dat we maar beperkte data tot onze beschikking hebben en de toetsen onderling niet kunnen vergelijken op een gedetailleerder niveau dan in bovenstaande tabel met toetsadviezen, onderzoeken we drie methoden voor om de eindtoetsscores te uniformeren:
Methode 1: Z-scores
Ten eerste kunnen we z-scores berekenen per toetsaanbieder, zodat de scores per toetsaanbieder allemaal een standaard normale verdeling krijgen, met een gemiddelde van 0 en standaarddeviatie van 1. Bij deze berekening houden we geen rekening met de toetsadviezen.
Deze aanpak past het beste als de onderliggende scores per toetsaanbieder ongeveer normaal verdeeld zijn. We zien echter in de data dat dit niet het geval is, zie figuren 5.2.2 tot en met 5.2.6.
| Eindtoetsscore | Dichtheid (Dichtheid) |
|---|---|
| 50 | 0,00426 |
| 50,21082 | 0,00451 |
| 50,32174 | 0,00474 |
| 50,43265 | 0,00495 |
| 50,54357 | 0,00514 |
| 50,65448 | 0,00529 |
| 50,76539 | 0,00542 |
| 50,87631 | 0,00551 |
| 50,98722 | 0,00558 |
| 51,09813 | 0,00561 |
| 51,20905 | 0,00562 |
| 51,31996 | 0,0056 |
| 51,43087 | 0,00555 |
| 51,54179 | 0,00547 |
| 51,6527 | 0,00538 |
| 51,76361 | 0,00527 |
| 51,87453 | 0,00516 |
| 51,98544 | 0,00503 |
| 52,09635 | 0,0049 |
| 52,20727 | 0,00477 |
| 52,31818 | 0,00464 |
| 52,4291 | 0,00452 |
| 52,54001 | 0,00441 |
| 52,65092 | 0,0043 |
| 52,76184 | 0,00421 |
| 52,87275 | 0,00412 |
| 52,98366 | 0,00405 |
| 53,09458 | 0,00399 |
| 53,20549 | 0,00395 |
| 53,3164 | 0,00391 |
| 53,42732 | 0,00388 |
| 53,53823 | 0,00387 |
| 53,64914 | 0,00386 |
| 53,76006 | 0,00386 |
| 53,87097 | 0,00387 |
| 53,98188 | 0,00389 |
| 54,0928 | 0,00391 |
| 54,20371 | 0,00394 |
| 54,31463 | 0,00397 |
| 54,42554 | 0,00401 |
| 54,53645 | 0,00405 |
| 54,64737 | 0,00409 |
| 54,75828 | 0,00414 |
| 54,86919 | 0,00419 |
| 54,98011 | 0,00424 |
| 55,09102 | 0,00429 |
| 55,20193 | 0,00434 |
| 55,31285 | 0,0044 |
| 55,42376 | 0,00446 |
| 55,53467 | 0,00452 |
| 55,64559 | 0,00458 |
| 55,7565 | 0,00465 |
| 55,86741 | 0,00471 |
| 55,97833 | 0,00478 |
| 56,08924 | 0,00485 |
| 56,20016 | 0,00491 |
| 56,31107 | 0,00498 |
| 56,42198 | 0,00505 |
| 56,5329 | 0,00512 |
| 56,64381 | 0,00519 |
| 56,75472 | 0,00526 |
| 56,86564 | 0,00532 |
| 56,97655 | 0,00539 |
| 57,08746 | 0,00546 |
| 57,19838 | 0,00552 |
| 57,30929 | 0,00558 |
| 57,4202 | 0,00565 |
| 57,53112 | 0,00571 |
| 57,64203 | 0,00577 |
| 57,75294 | 0,00584 |
| 57,86386 | 0,0059 |
| 57,97477 | 0,00596 |
| 58,08569 | 0,00603 |
| 58,1966 | 0,00609 |
| 58,30751 | 0,00616 |
| 58,41843 | 0,00622 |
| 58,52934 | 0,00629 |
| 58,64025 | 0,00636 |
| 58,75117 | 0,00644 |
| 58,86208 | 0,00651 |
| 58,97299 | 0,00658 |
| 59,08391 | 0,00666 |
| 59,19482 | 0,00673 |
| 59,30573 | 0,00681 |
| 59,41665 | 0,00688 |
| 59,52756 | 0,00696 |
| 59,63848 | 0,00703 |
| 59,74939 | 0,00711 |
| 59,8603 | 0,00718 |
| 59,97122 | 0,00725 |
| 60,08213 | 0,00733 |
| 60,19304 | 0,0074 |
| 60,30396 | 0,00747 |
| 60,41487 | 0,00755 |
| 60,52578 | 0,00763 |
| 60,6367 | 0,0077 |
| 60,74761 | 0,00779 |
| 60,85852 | 0,00787 |
| 60,96944 | 0,00796 |
| 61,08035 | 0,00805 |
| 61,19126 | 0,00814 |
| 61,30218 | 0,00824 |
| 61,41309 | 0,00834 |
| 61,52401 | 0,00845 |
| 61,63492 | 0,00856 |
| 61,74583 | 0,00867 |
| 61,85675 | 0,00879 |
| 61,96766 | 0,0089 |
| 62,07857 | 0,00902 |
| 62,18949 | 0,00914 |
| 62,3004 | 0,00927 |
| 62,41131 | 0,00939 |
| 62,52223 | 0,00951 |
| 62,63314 | 0,00964 |
| 62,74405 | 0,00976 |
| 62,85497 | 0,00988 |
| 62,96588 | 0,01 |
| 63,07679 | 0,01012 |
| 63,18771 | 0,01024 |
| 63,29862 | 0,01036 |
| 63,40954 | 0,01048 |
| 63,52045 | 0,01059 |
| 63,63136 | 0,0107 |
| 63,74228 | 0,01081 |
| 63,85319 | 0,01091 |
| 63,9641 | 0,01101 |
| 64,07502 | 0,01111 |
| 64,18593 | 0,0112 |
| 64,29684 | 0,01129 |
| 64,40776 | 0,01138 |
| 64,51867 | 0,01146 |
| 64,62958 | 0,01153 |
| 64,7405 | 0,01161 |
| 64,85141 | 0,01168 |
| 64,96232 | 0,01174 |
| 65,07324 | 0,01181 |
| 65,18415 | 0,01187 |
| 65,29507 | 0,01193 |
| 65,40598 | 0,01199 |
| 65,51689 | 0,01205 |
| 65,62781 | 0,01211 |
| 65,73872 | 0,01216 |
| 65,84963 | 0,01222 |
| 65,96055 | 0,01228 |
| 66,07146 | 0,01235 |
| 66,18237 | 0,01242 |
| 66,29329 | 0,01249 |
| 66,4042 | 0,01257 |
| 66,51511 | 0,01266 |
| 66,62603 | 0,01277 |
| 66,73694 | 0,01288 |
| 66,84786 | 0,01301 |
| 66,95877 | 0,01316 |
| 67,06968 | 0,01333 |
| 67,1806 | 0,01352 |
| 67,29151 | 0,01373 |
| 67,40242 | 0,01396 |
| 67,51334 | 0,01421 |
| 67,62425 | 0,01449 |
| 67,73516 | 0,01479 |
| 67,84608 | 0,01511 |
| 67,95699 | 0,01545 |
| 68,0679 | 0,01581 |
| 68,17882 | 0,01619 |
| 68,28973 | 0,01657 |
| 68,40064 | 0,01697 |
| 68,51156 | 0,01737 |
| 68,62247 | 0,01778 |
| 68,73339 | 0,01818 |
| 68,8443 | 0,01858 |
| 68,95521 | 0,01897 |
| 69,06613 | 0,01934 |
| 69,17704 | 0,01971 |
| 69,28795 | 0,02006 |
| 69,39887 | 0,02039 |
| 69,50978 | 0,0207 |
| 69,62069 | 0,02099 |
| 69,73161 | 0,02126 |
| 69,84252 | 0,02152 |
| 69,95343 | 0,02176 |
| 70,06435 | 0,02198 |
| 70,17526 | 0,02218 |
| 70,28617 | 0,02237 |
| 70,39709 | 0,02255 |
| 70,508 | 0,02272 |
| 70,61892 | 0,02288 |
| 70,72983 | 0,02304 |
| 70,84074 | 0,02319 |
| 70,95166 | 0,02334 |
| 71,06257 | 0,02349 |
| 71,17348 | 0,02365 |
| 71,2844 | 0,02381 |
| 71,39531 | 0,02397 |
| 71,50622 | 0,02414 |
| 71,61714 | 0,02432 |
| 71,72805 | 0,0245 |
| 71,83896 | 0,0247 |
| 71,94988 | 0,0249 |
| 72,06079 | 0,02511 |
| 72,1717 | 0,02532 |
| 72,28262 | 0,02554 |
| 72,39353 | 0,02576 |
| 72,50445 | 0,02599 |
| 72,61536 | 0,02622 |
| 72,72627 | 0,02644 |
| 72,83719 | 0,02666 |
| 72,9481 | 0,02689 |
| 73,05901 | 0,0271 |
| 73,16993 | 0,02731 |
| 73,28084 | 0,02752 |
| 73,39175 | 0,02772 |
| 73,50267 | 0,02791 |
| 73,61358 | 0,02809 |
| 73,72449 | 0,02827 |
| 73,83541 | 0,02845 |
| 73,94632 | 0,02861 |
| 74,05723 | 0,02878 |
| 74,16815 | 0,02894 |
| 74,27906 | 0,0291 |
| 74,38998 | 0,02926 |
| 74,50089 | 0,02943 |
| 74,6118 | 0,02959 |
| 74,72272 | 0,02976 |
| 74,83363 | 0,02993 |
| 74,94454 | 0,0301 |
| 75,05546 | 0,03028 |
| 75,16637 | 0,03047 |
| 75,27728 | 0,03066 |
| 75,3882 | 0,03086 |
| 75,49911 | 0,03106 |
| 75,61002 | 0,03127 |
| 75,72094 | 0,03148 |
| 75,83185 | 0,03169 |
| 75,94277 | 0,03191 |
| 76,05368 | 0,03213 |
| 76,16459 | 0,03236 |
| 76,27551 | 0,03258 |
| 76,38642 | 0,0328 |
| 76,49733 | 0,03302 |
| 76,60825 | 0,03324 |
| 76,71916 | 0,03345 |
| 76,83007 | 0,03367 |
| 76,94099 | 0,03387 |
| 77,0519 | 0,03407 |
| 77,16281 | 0,03427 |
| 77,27373 | 0,03446 |
| 77,38464 | 0,03465 |
| 77,49555 | 0,03483 |
| 77,60647 | 0,035 |
| 77,71738 | 0,03517 |
| 77,8283 | 0,03533 |
| 77,93921 | 0,03549 |
| 78,05012 | 0,03564 |
| 78,16104 | 0,03578 |
| 78,27195 | 0,03592 |
| 78,38286 | 0,03605 |
| 78,49378 | 0,03617 |
| 78,60469 | 0,03629 |
| 78,7156 | 0,03639 |
| 78,82652 | 0,03649 |
| 78,93743 | 0,03658 |
| 79,04834 | 0,03666 |
| 79,15926 | 0,03673 |
| 79,27017 | 0,03679 |
| 79,38108 | 0,03684 |
| 79,492 | 0,03689 |
| 79,60291 | 0,03692 |
| 79,71383 | 0,03695 |
| 79,82474 | 0,03697 |
| 79,93565 | 0,03698 |
| 80,04657 | 0,03699 |
| 80,15748 | 0,03699 |
| 80,26839 | 0,03699 |
| 80,37931 | 0,03698 |
| 80,49022 | 0,03697 |
| 80,60113 | 0,03697 |
| 80,71205 | 0,03696 |
| 80,82296 | 0,03695 |
| 80,93387 | 0,03695 |
| 81,04479 | 0,03695 |
| 81,1557 | 0,03695 |
| 81,26661 | 0,03695 |
| 81,37753 | 0,03695 |
| 81,48844 | 0,03696 |
| 81,59936 | 0,03696 |
| 81,71027 | 0,03696 |
| 81,82118 | 0,03696 |
| 81,9321 | 0,03696 |
| 82,04301 | 0,03695 |
| 82,15392 | 0,03693 |
| 82,26484 | 0,0369 |
| 82,37575 | 0,03687 |
| 82,48666 | 0,03682 |
| 82,59758 | 0,03675 |
| 82,70849 | 0,03667 |
| 82,8194 | 0,03658 |
| 82,93032 | 0,03647 |
| 83,04123 | 0,03634 |
| 83,15214 | 0,0362 |
| 83,26306 | 0,03604 |
| 83,37397 | 0,03586 |
| 83,48489 | 0,03566 |
| 83,5958 | 0,03545 |
| 83,70671 | 0,03522 |
| 83,81763 | 0,03498 |
| 83,92854 | 0,03473 |
| 84,03945 | 0,03447 |
| 84,15037 | 0,0342 |
| 84,26128 | 0,03392 |
| 84,37219 | 0,03365 |
| 84,48311 | 0,03337 |
| 84,59402 | 0,03309 |
| 84,70493 | 0,03281 |
| 84,81585 | 0,03253 |
| 84,92676 | 0,03227 |
| 85,03768 | 0,032 |
| 85,14859 | 0,03175 |
| 85,2595 | 0,0315 |
| 85,37042 | 0,03126 |
| 85,48133 | 0,03102 |
| 85,59224 | 0,0308 |
| 85,70316 | 0,03058 |
| 85,81407 | 0,03037 |
| 85,92498 | 0,03017 |
| 86,0359 | 0,02997 |
| 86,14681 | 0,02978 |
| 86,25772 | 0,0296 |
| 86,36864 | 0,02942 |
| 86,47955 | 0,02924 |
| 86,59046 | 0,02907 |
| 86,70138 | 0,02891 |
| 86,81229 | 0,02874 |
| 86,92321 | 0,02858 |
| 87,03412 | 0,02842 |
| 87,14503 | 0,02826 |
| 87,25595 | 0,0281 |
| 87,36686 | 0,02794 |
| 87,47777 | 0,02778 |
| 87,58869 | 0,02761 |
| 87,6996 | 0,02744 |
| 87,81051 | 0,02726 |
| 87,92143 | 0,02708 |
| 88,03234 | 0,02689 |
| 88,14325 | 0,02669 |
| 88,25417 | 0,02649 |
| 88,36508 | 0,02628 |
| 88,47599 | 0,02607 |
| 88,58691 | 0,02586 |
| 88,69782 | 0,02564 |
| 88,80874 | 0,02542 |
| 88,91965 | 0,0252 |
| 89,03056 | 0,02498 |
| 89,14148 | 0,02477 |
| 89,25239 | 0,02456 |
| 89,3633 | 0,02435 |
| 89,47422 | 0,02415 |
| 89,58513 | 0,02396 |
| 89,69604 | 0,02378 |
| 89,80696 | 0,02361 |
| 89,91787 | 0,02344 |
| 90,02878 | 0,02328 |
| 90,1397 | 0,02313 |
| 90,25061 | 0,02299 |
| 90,36152 | 0,02285 |
| 90,47244 | 0,02272 |
| 90,58335 | 0,02258 |
| 90,69427 | 0,02245 |
| 90,80518 | 0,02231 |
| 90,91609 | 0,02217 |
| 91,02701 | 0,02203 |
| 91,13792 | 0,02188 |
| 91,24883 | 0,02172 |
| 91,35975 | 0,02155 |
| 91,47066 | 0,02138 |
| 91,58157 | 0,02119 |
| 91,69249 | 0,021 |
| 91,8034 | 0,0208 |
| 91,91431 | 0,02059 |
| 92,02523 | 0,02037 |
| 92,13614 | 0,02015 |
| 92,24706 | 0,01992 |
| 92,35797 | 0,01969 |
| 92,46888 | 0,01946 |
| 92,5798 | 0,01923 |
| 92,69071 | 0,019 |
| 92,80162 | 0,01877 |
| 92,91254 | 0,01854 |
| 93,02345 | 0,01832 |
| 93,13436 | 0,0181 |
| 93,24528 | 0,01789 |
| 93,35619 | 0,01769 |
| 93,4671 | 0,01748 |
| 93,57802 | 0,01729 |
| 93,68893 | 0,0171 |
| 93,79984 | 0,01691 |
| 93,91076 | 0,01673 |
| 94,02167 | 0,01654 |
| 94,13259 | 0,01637 |
| 94,2435 | 0,01619 |
| 94,35441 | 0,01601 |
| 94,46533 | 0,01584 |
| 94,57624 | 0,01566 |
| 94,68715 | 0,01548 |
| 94,79807 | 0,0153 |
| 94,90898 | 0,01511 |
| 95,01989 | 0,01493 |
| 95,13081 | 0,01474 |
| 95,24172 | 0,01455 |
| 95,35263 | 0,01436 |
| 95,46355 | 0,01416 |
| 95,57446 | 0,01397 |
| 95,68537 | 0,01378 |
| 95,79629 | 0,01358 |
| 95,9072 | 0,01339 |
| 96,01812 | 0,01321 |
| 96,12903 | 0,01303 |
| 96,23994 | 0,01285 |
| 96,35086 | 0,01269 |
| 96,46177 | 0,01254 |
| 96,57268 | 0,0124 |
| 96,6836 | 0,01228 |
| 96,79451 | 0,01217 |
| 96,90542 | 0,01209 |
| 97,01634 | 0,01204 |
| 97,12725 | 0,01202 |
| 97,23816 | 0,01204 |
| 97,34908 | 0,0121 |
| 97,45999 | 0,01221 |
| 97,5709 | 0,01237 |
| 97,68182 | 0,01258 |
| 97,79273 | 0,01285 |
| 97,90365 | 0,01318 |
| 98,01456 | 0,01359 |
| 98,12547 | 0,01406 |
| 98,23639 | 0,01459 |
| 98,3473 | 0,01518 |
| 98,45821 | 0,01582 |
| 98,56913 | 0,01651 |
| 98,68004 | 0,01723 |
| 98,79095 | 0,01797 |
| 98,90187 | 0,0187 |
| 99,01278 | 0,01942 |
| 99,12369 | 0,0201 |
| 99,23461 | 0,02072 |
| 99,34552 | 0,02126 |
| 99,45643 | 0,0217 |
| 99,56735 | 0,02201 |
| 99,67826 | 0,02217 |
| 99,78918 | 0,02218 |
| 100 | 0,02204 |
| Eindtoetsscore | Dichtheid (Dichtheid) |
|---|---|
| 501 | 0,00047 |
| 501,12461 | 0,00049 |
| 501,23129 | 0,00051 |
| 501,33796 | 0,00052 |
| 501,44464 | 0,00054 |
| 501,55131 | 0,00055 |
| 501,65799 | 0,00055 |
| 501,76466 | 0,00056 |
| 501,87134 | 0,00056 |
| 501,97802 | 0,00057 |
| 502,08469 | 0,00057 |
| 502,19137 | 0,00057 |
| 502,29804 | 0,00058 |
| 502,40472 | 0,00058 |
| 502,51139 | 0,00059 |
| 502,61807 | 0,00059 |
| 502,72474 | 0,0006 |
| 502,83142 | 0,00061 |
| 502,9381 | 0,00062 |
| 503,04477 | 0,00063 |
| 503,15145 | 0,00065 |
| 503,25812 | 0,00066 |
| 503,3648 | 0,00067 |
| 503,47147 | 0,00069 |
| 503,57815 | 0,00071 |
| 503,68483 | 0,00072 |
| 503,7915 | 0,00074 |
| 503,89818 | 0,00076 |
| 504,00485 | 0,00078 |
| 504,11153 | 0,0008 |
| 504,2182 | 0,00082 |
| 504,32488 | 0,00084 |
| 504,43156 | 0,00087 |
| 504,53823 | 0,00089 |
| 504,64491 | 0,00092 |
| 504,75158 | 0,00094 |
| 504,85826 | 0,00097 |
| 504,96493 | 0,001 |
| 505,07161 | 0,00103 |
| 505,17829 | 0,00106 |
| 505,28496 | 0,00109 |
| 505,39164 | 0,00112 |
| 505,49831 | 0,00115 |
| 505,60499 | 0,00118 |
| 505,71166 | 0,00121 |
| 505,81834 | 0,00124 |
| 505,92501 | 0,00127 |
| 506,03169 | 0,0013 |
| 506,13837 | 0,00133 |
| 506,24504 | 0,00135 |
| 506,35172 | 0,00138 |
| 506,45839 | 0,00141 |
| 506,56507 | 0,00143 |
| 506,67174 | 0,00146 |
| 506,77842 | 0,00148 |
| 506,8851 | 0,00151 |
| 506,99177 | 0,00154 |
| 507,09845 | 0,00157 |
| 507,20512 | 0,0016 |
| 507,3118 | 0,00163 |
| 507,41847 | 0,00166 |
| 507,52515 | 0,0017 |
| 507,63183 | 0,00174 |
| 507,7385 | 0,00178 |
| 507,84518 | 0,00182 |
| 507,95185 | 0,00187 |
| 508,05853 | 0,00191 |
| 508,1652 | 0,00196 |
| 508,27188 | 0,00202 |
| 508,37856 | 0,00207 |
| 508,48523 | 0,00212 |
| 508,59191 | 0,00218 |
| 508,69858 | 0,00224 |
| 508,80526 | 0,0023 |
| 508,91193 | 0,00236 |
| 509,01861 | 0,00242 |
| 509,12528 | 0,00248 |
| 509,23196 | 0,00255 |
| 509,33864 | 0,00261 |
| 509,44531 | 0,00267 |
| 509,55199 | 0,00274 |
| 509,65866 | 0,0028 |
| 509,76534 | 0,00286 |
| 509,87201 | 0,00293 |
| 509,97869 | 0,003 |
| 510,08537 | 0,00306 |
| 510,19204 | 0,00313 |
| 510,29872 | 0,00319 |
| 510,40539 | 0,00326 |
| 510,51207 | 0,00333 |
| 510,61874 | 0,0034 |
| 510,72542 | 0,00346 |
| 510,8321 | 0,00353 |
| 510,93877 | 0,0036 |
| 511,04545 | 0,00367 |
| 511,15212 | 0,00373 |
| 511,2588 | 0,0038 |
| 511,36547 | 0,00387 |
| 511,47215 | 0,00394 |
| 511,57883 | 0,00401 |
| 511,6855 | 0,00408 |
| 511,79218 | 0,00415 |
| 511,89885 | 0,00422 |
| 512,00553 | 0,0043 |
| 512,1122 | 0,00437 |
| 512,21888 | 0,00445 |
| 512,32555 | 0,00452 |
| 512,43223 | 0,0046 |
| 512,53891 | 0,00468 |
| 512,64558 | 0,00476 |
| 512,75226 | 0,00484 |
| 512,85893 | 0,00493 |
| 512,96561 | 0,00501 |
| 513,07228 | 0,00509 |
| 513,17896 | 0,00518 |
| 513,28564 | 0,00526 |
| 513,39231 | 0,00535 |
| 513,49899 | 0,00543 |
| 513,60566 | 0,00552 |
| 513,71234 | 0,0056 |
| 513,81901 | 0,00569 |
| 513,92569 | 0,00577 |
| 514,03237 | 0,00586 |
| 514,13904 | 0,00595 |
| 514,24572 | 0,00604 |
| 514,35239 | 0,00613 |
| 514,45907 | 0,00623 |
| 514,56574 | 0,00632 |
| 514,67242 | 0,00643 |
| 514,7791 | 0,00653 |
| 514,88577 | 0,00664 |
| 514,99245 | 0,00676 |
| 515,09912 | 0,00688 |
| 515,2058 | 0,007 |
| 515,31247 | 0,00712 |
| 515,41915 | 0,00725 |
| 515,52583 | 0,00738 |
| 515,6325 | 0,00752 |
| 515,73918 | 0,00765 |
| 515,84585 | 0,00779 |
| 515,95253 | 0,00792 |
| 516,0592 | 0,00806 |
| 516,16588 | 0,00819 |
| 516,27255 | 0,00832 |
| 516,37923 | 0,00845 |
| 516,48591 | 0,00857 |
| 516,59258 | 0,00869 |
| 516,69926 | 0,00881 |
| 516,80593 | 0,00893 |
| 516,91261 | 0,00904 |
| 517,01928 | 0,00915 |
| 517,12596 | 0,00925 |
| 517,23264 | 0,00936 |
| 517,33931 | 0,00946 |
| 517,44599 | 0,00956 |
| 517,55266 | 0,00967 |
| 517,65934 | 0,00977 |
| 517,76601 | 0,00988 |
| 517,87269 | 0,00998 |
| 517,97937 | 0,01009 |
| 518,08604 | 0,0102 |
| 518,19272 | 0,01032 |
| 518,29939 | 0,01044 |
| 518,40607 | 0,01056 |
| 518,51274 | 0,01068 |
| 518,61942 | 0,01081 |
| 518,7261 | 0,01094 |
| 518,83277 | 0,01108 |
| 518,93945 | 0,01121 |
| 519,04612 | 0,01135 |
| 519,1528 | 0,01149 |
| 519,25947 | 0,01163 |
| 519,36615 | 0,01177 |
| 519,47282 | 0,0119 |
| 519,5795 | 0,01204 |
| 519,68618 | 0,01218 |
| 519,79285 | 0,01231 |
| 519,89953 | 0,01244 |
| 520,0062 | 0,01257 |
| 520,11288 | 0,0127 |
| 520,21955 | 0,01283 |
| 520,32623 | 0,01296 |
| 520,43291 | 0,01309 |
| 520,53958 | 0,01322 |
| 520,64626 | 0,01335 |
| 520,75293 | 0,01349 |
| 520,85961 | 0,01362 |
| 520,96628 | 0,01376 |
| 521,07296 | 0,01391 |
| 521,17964 | 0,01406 |
| 521,28631 | 0,01421 |
| 521,39299 | 0,01436 |
| 521,49966 | 0,01453 |
| 521,60634 | 0,01469 |
| 521,71301 | 0,01486 |
| 521,81969 | 0,01503 |
| 521,92637 | 0,0152 |
| 522,03304 | 0,01538 |
| 522,13972 | 0,01555 |
| 522,24639 | 0,01573 |
| 522,35307 | 0,01591 |
| 522,45974 | 0,01608 |
| 522,56642 | 0,01626 |
| 522,67309 | 0,01643 |
| 522,77977 | 0,0166 |
| 522,88645 | 0,01677 |
| 522,99312 | 0,01694 |
| 523,0998 | 0,0171 |
| 523,20647 | 0,01726 |
| 523,31315 | 0,01742 |
| 523,41982 | 0,01758 |
| 523,5265 | 0,01774 |
| 523,63318 | 0,0179 |
| 523,73985 | 0,01806 |
| 523,84653 | 0,01822 |
| 523,9532 | 0,01838 |
| 524,05988 | 0,01854 |
| 524,16655 | 0,0187 |
| 524,27323 | 0,01886 |
| 524,37991 | 0,01903 |
| 524,48658 | 0,0192 |
| 524,59326 | 0,01937 |
| 524,69993 | 0,01955 |
| 524,80661 | 0,01973 |
| 524,91328 | 0,01991 |
| 525,01996 | 0,0201 |
| 525,12664 | 0,02029 |
| 525,23331 | 0,02048 |
| 525,33999 | 0,02067 |
| 525,44666 | 0,02087 |
| 525,55334 | 0,02107 |
| 525,66001 | 0,02127 |
| 525,76669 | 0,02147 |
| 525,87336 | 0,02167 |
| 525,98004 | 0,02187 |
| 526,08672 | 0,02207 |
| 526,19339 | 0,02226 |
| 526,30007 | 0,02246 |
| 526,40674 | 0,02265 |
| 526,51342 | 0,02284 |
| 526,62009 | 0,02302 |
| 526,72677 | 0,0232 |
| 526,83345 | 0,02338 |
| 526,94012 | 0,02355 |
| 527,0468 | 0,02372 |
| 527,15347 | 0,02388 |
| 527,26015 | 0,02404 |
| 527,36682 | 0,0242 |
| 527,4735 | 0,02436 |
| 527,58018 | 0,02452 |
| 527,68685 | 0,02468 |
| 527,79353 | 0,02484 |
| 527,9002 | 0,02501 |
| 528,00688 | 0,02517 |
| 528,11355 | 0,02535 |
| 528,22023 | 0,02553 |
| 528,32691 | 0,02571 |
| 528,43358 | 0,02589 |
| 528,54026 | 0,02608 |
| 528,64693 | 0,02627 |
| 528,75361 | 0,02647 |
| 528,86028 | 0,02666 |
| 528,96696 | 0,02686 |
| 529,07363 | 0,02706 |
| 529,18031 | 0,02726 |
| 529,28699 | 0,02745 |
| 529,39366 | 0,02765 |
| 529,50034 | 0,02785 |
| 529,60701 | 0,02805 |
| 529,71369 | 0,02825 |
| 529,82036 | 0,02845 |
| 529,92704 | 0,02865 |
| 530,03372 | 0,02885 |
| 530,14039 | 0,02905 |
| 530,24707 | 0,02925 |
| 530,35374 | 0,02945 |
| 530,46042 | 0,02964 |
| 530,56709 | 0,02983 |
| 530,67377 | 0,03002 |
| 530,78045 | 0,0302 |
| 530,88712 | 0,03037 |
| 530,9938 | 0,03054 |
| 531,10047 | 0,0307 |
| 531,20715 | 0,03085 |
| 531,31382 | 0,031 |
| 531,4205 | 0,03114 |
| 531,52718 | 0,03127 |
| 531,63385 | 0,03139 |
| 531,74053 | 0,03151 |
| 531,8472 | 0,03163 |
| 531,95388 | 0,03174 |
| 532,06055 | 0,03185 |
| 532,16723 | 0,03196 |
| 532,2739 | 0,03206 |
| 532,38058 | 0,03217 |
| 532,48726 | 0,03229 |
| 532,59393 | 0,0324 |
| 532,70061 | 0,03252 |
| 532,80728 | 0,03265 |
| 532,91396 | 0,03278 |
| 533,02063 | 0,03292 |
| 533,12731 | 0,03307 |
| 533,23399 | 0,03322 |
| 533,34066 | 0,03338 |
| 533,44734 | 0,03354 |
| 533,55401 | 0,03372 |
| 533,66069 | 0,0339 |
| 533,76736 | 0,03408 |
| 533,87404 | 0,03428 |
| 533,98072 | 0,03447 |
| 534,08739 | 0,03467 |
| 534,19407 | 0,03487 |
| 534,30074 | 0,03507 |
| 534,40742 | 0,03527 |
| 534,51409 | 0,03547 |
| 534,62077 | 0,03567 |
| 534,72745 | 0,03586 |
| 534,83412 | 0,03605 |
| 534,9408 | 0,03623 |
| 535,04747 | 0,03641 |
| 535,15415 | 0,03659 |
| 535,26082 | 0,03676 |
| 535,3675 | 0,03693 |
| 535,47417 | 0,03709 |
| 535,58085 | 0,03726 |
| 535,68753 | 0,03743 |
| 535,7942 | 0,0376 |
| 535,90088 | 0,03777 |
| 536,00755 | 0,03794 |
| 536,11423 | 0,03812 |
| 536,2209 | 0,0383 |
| 536,32758 | 0,03849 |
| 536,43426 | 0,03868 |
| 536,54093 | 0,03888 |
| 536,64761 | 0,03907 |
| 536,75428 | 0,03927 |
| 536,86096 | 0,03946 |
| 536,96763 | 0,03965 |
| 537,07431 | 0,03984 |
| 537,18099 | 0,04002 |
| 537,28766 | 0,04019 |
| 537,39434 | 0,04035 |
| 537,50101 | 0,0405 |
| 537,60769 | 0,04063 |
| 537,71436 | 0,04075 |
| 537,82104 | 0,04086 |
| 537,92772 | 0,04095 |
| 538,03439 | 0,04102 |
| 538,14107 | 0,04107 |
| 538,24774 | 0,0411 |
| 538,35442 | 0,04112 |
| 538,46109 | 0,04112 |
| 538,56777 | 0,04111 |
| 538,67445 | 0,04108 |
| 538,78112 | 0,04104 |
| 538,8878 | 0,04099 |
| 538,99447 | 0,04093 |
| 539,10115 | 0,04087 |
| 539,20782 | 0,04081 |
| 539,3145 | 0,04074 |
| 539,42117 | 0,04069 |
| 539,52785 | 0,04063 |
| 539,63453 | 0,04059 |
| 539,7412 | 0,04055 |
| 539,84788 | 0,04053 |
| 539,95455 | 0,04052 |
| 540,06123 | 0,04052 |
| 540,1679 | 0,04054 |
| 540,27458 | 0,04057 |
| 540,38126 | 0,0406 |
| 540,48793 | 0,04065 |
| 540,59461 | 0,0407 |
| 540,70128 | 0,04075 |
| 540,80796 | 0,04081 |
| 540,91463 | 0,04086 |
| 541,02131 | 0,04091 |
| 541,12799 | 0,04095 |
| 541,23466 | 0,04098 |
| 541,34134 | 0,041 |
| 541,44801 | 0,041 |
| 541,55469 | 0,041 |
| 541,66136 | 0,04098 |
| 541,76804 | 0,04094 |
| 541,87472 | 0,04089 |
| 541,98139 | 0,04083 |
| 542,08807 | 0,04074 |
| 542,19474 | 0,04065 |
| 542,30142 | 0,04053 |
| 542,40809 | 0,0404 |
| 542,51477 | 0,04026 |
| 542,62144 | 0,0401 |
| 542,72812 | 0,03992 |
| 542,8348 | 0,03974 |
| 542,94147 | 0,03954 |
| 543,04815 | 0,03933 |
| 543,15482 | 0,03911 |
| 543,2615 | 0,03889 |
| 543,36817 | 0,03866 |
| 543,47485 | 0,03843 |
| 543,58153 | 0,03819 |
| 543,6882 | 0,03796 |
| 543,79488 | 0,03774 |
| 543,90155 | 0,03751 |
| 544,00823 | 0,0373 |
| 544,1149 | 0,03708 |
| 544,22158 | 0,03687 |
| 544,32826 | 0,03666 |
| 544,43493 | 0,03645 |
| 544,54161 | 0,03624 |
| 544,64828 | 0,03603 |
| 544,75496 | 0,0358 |
| 544,86163 | 0,03557 |
| 544,96831 | 0,03533 |
| 545,07499 | 0,03508 |
| 545,18166 | 0,03481 |
| 545,28834 | 0,03452 |
| 545,39501 | 0,03422 |
| 545,50169 | 0,0339 |
| 545,60836 | 0,03356 |
| 545,71504 | 0,0332 |
| 545,82171 | 0,03283 |
| 545,92839 | 0,03245 |
| 546,03507 | 0,03205 |
| 546,14174 | 0,03164 |
| 546,24842 | 0,03122 |
| 546,35509 | 0,03079 |
| 546,46177 | 0,03035 |
| 546,56844 | 0,02991 |
| 546,67512 | 0,02947 |
| 546,7818 | 0,02902 |
| 546,88847 | 0,02858 |
| 546,99515 | 0,02813 |
| 547,10182 | 0,02769 |
| 547,2085 | 0,02726 |
| 547,31517 | 0,02683 |
| 547,42185 | 0,02641 |
| 547,52853 | 0,02601 |
| 547,6352 | 0,02562 |
| 547,74188 | 0,02525 |
| 547,84855 | 0,02491 |
| 547,95523 | 0,02459 |
| 548,0619 | 0,02431 |
| 548,16858 | 0,02407 |
| 548,27526 | 0,02387 |
| 548,38193 | 0,02371 |
| 548,48861 | 0,02359 |
| 548,59528 | 0,02352 |
| 548,70196 | 0,02347 |
| 548,80863 | 0,02346 |
| 548,91531 | 0,02347 |
| 549,02198 | 0,02348 |
| 549,12866 | 0,02348 |
| 549,23534 | 0,02345 |
| 549,34201 | 0,02337 |
| 549,44869 | 0,02321 |
| 549,55536 | 0,02297 |
| 549,66204 | 0,02262 |
| 549,76871 | 0,02215 |
| 549,87539 | 0,02154 |
| 550 | 0,02078 |
| Eindtoetsscore | Dichtheid (Dichtheid) |
|---|---|
| 100 | 0,00475 |
| 100,73405 | 0,00479 |
| 101,18836 | 0,00481 |
| 101,64266 | 0,0048 |
| 102,09697 | 0,00477 |
| 102,55128 | 0,00472 |
| 103,00558 | 0,00465 |
| 103,45989 | 0,00456 |
| 103,9142 | 0,00445 |
| 104,3685 | 0,00434 |
| 104,82281 | 0,00421 |
| 105,27712 | 0,00408 |
| 105,73142 | 0,00394 |
| 106,18573 | 0,00381 |
| 106,64003 | 0,00367 |
| 107,09434 | 0,00354 |
| 107,54865 | 0,00341 |
| 108,00295 | 0,00329 |
| 108,45726 | 0,00318 |
| 108,91157 | 0,00308 |
| 109,36587 | 0,00298 |
| 109,82018 | 0,0029 |
| 110,27449 | 0,00282 |
| 110,72879 | 0,00276 |
| 111,1831 | 0,0027 |
| 111,6374 | 0,00265 |
| 112,09171 | 0,00261 |
| 112,54602 | 0,00258 |
| 113,00032 | 0,00256 |
| 113,45463 | 0,00254 |
| 113,90894 | 0,00253 |
| 114,36324 | 0,00252 |
| 114,81755 | 0,00252 |
| 115,27186 | 0,00252 |
| 115,72616 | 0,00252 |
| 116,18047 | 0,00253 |
| 116,63478 | 0,00254 |
| 117,08908 | 0,00256 |
| 117,54339 | 0,00257 |
| 117,99769 | 0,00259 |
| 118,452 | 0,00261 |
| 118,90631 | 0,00263 |
| 119,36061 | 0,00266 |
| 119,81492 | 0,00268 |
| 120,26923 | 0,00271 |
| 120,72353 | 0,00273 |
| 121,17784 | 0,00276 |
| 121,63215 | 0,00279 |
| 122,08645 | 0,00282 |
| 122,54076 | 0,00285 |
| 122,99506 | 0,00288 |
| 123,44937 | 0,00291 |
| 123,90368 | 0,00294 |
| 124,35798 | 0,00297 |
| 124,81229 | 0,003 |
| 125,2666 | 0,00303 |
| 125,7209 | 0,00306 |
| 126,17521 | 0,00309 |
| 126,62952 | 0,00312 |
| 127,08382 | 0,00315 |
| 127,53813 | 0,00318 |
| 127,99244 | 0,00321 |
| 128,44674 | 0,00324 |
| 128,90105 | 0,00327 |
| 129,35535 | 0,0033 |
| 129,80966 | 0,00333 |
| 130,26397 | 0,00336 |
| 130,71827 | 0,00339 |
| 131,17258 | 0,00342 |
| 131,62689 | 0,00345 |
| 132,08119 | 0,00349 |
| 132,5355 | 0,00352 |
| 132,98981 | 0,00355 |
| 133,44411 | 0,00358 |
| 133,89842 | 0,00361 |
| 134,35272 | 0,00365 |
| 134,80703 | 0,00368 |
| 135,26134 | 0,00371 |
| 135,71564 | 0,00375 |
| 136,16995 | 0,00378 |
| 136,62426 | 0,00381 |
| 137,07856 | 0,00385 |
| 137,53287 | 0,00388 |
| 137,98718 | 0,00392 |
| 138,44148 | 0,00395 |
| 138,89579 | 0,00398 |
| 139,3501 | 0,00401 |
| 139,8044 | 0,00405 |
| 140,25871 | 0,00408 |
| 140,71301 | 0,00411 |
| 141,16732 | 0,00415 |
| 141,62163 | 0,00418 |
| 142,07593 | 0,00421 |
| 142,53024 | 0,00424 |
| 142,98455 | 0,00428 |
| 143,43885 | 0,00431 |
| 143,89316 | 0,00434 |
| 144,34747 | 0,00438 |
| 144,80177 | 0,00441 |
| 145,25608 | 0,00445 |
| 145,71038 | 0,00448 |
| 146,16469 | 0,00452 |
| 146,619 | 0,00455 |
| 147,0733 | 0,00459 |
| 147,52761 | 0,00462 |
| 147,98192 | 0,00466 |
| 148,43622 | 0,0047 |
| 148,89053 | 0,00474 |
| 149,34484 | 0,00477 |
| 149,79914 | 0,00481 |
| 150,25345 | 0,00485 |
| 150,70776 | 0,00489 |
| 151,16206 | 0,00492 |
| 151,61637 | 0,00496 |
| 152,07067 | 0,005 |
| 152,52498 | 0,00504 |
| 152,97929 | 0,00507 |
| 153,43359 | 0,00511 |
| 153,8879 | 0,00514 |
| 154,34221 | 0,00518 |
| 154,79651 | 0,00521 |
| 155,25082 | 0,00524 |
| 155,70513 | 0,00528 |
| 156,15943 | 0,00531 |
| 156,61374 | 0,00534 |
| 157,06804 | 0,00537 |
| 157,52235 | 0,0054 |
| 157,97666 | 0,00543 |
| 158,43096 | 0,00546 |
| 158,88527 | 0,0055 |
| 159,33958 | 0,00553 |
| 159,79388 | 0,00556 |
| 160,24819 | 0,0056 |
| 160,7025 | 0,00563 |
| 161,1568 | 0,00567 |
| 161,61111 | 0,00571 |
| 162,06542 | 0,00574 |
| 162,51972 | 0,00578 |
| 162,97403 | 0,00583 |
| 163,42833 | 0,00587 |
| 163,88264 | 0,00591 |
| 164,33695 | 0,00596 |
| 164,79125 | 0,00601 |
| 165,24556 | 0,00606 |
| 165,69987 | 0,00611 |
| 166,15417 | 0,00616 |
| 166,60848 | 0,00621 |
| 167,06279 | 0,00626 |
| 167,51709 | 0,00632 |
| 167,9714 | 0,00637 |
| 168,42571 | 0,00642 |
| 168,88001 | 0,00648 |
| 169,33432 | 0,00654 |
| 169,78862 | 0,00659 |
| 170,24293 | 0,00665 |
| 170,69724 | 0,0067 |
| 171,15154 | 0,00676 |
| 171,60585 | 0,00681 |
| 172,06016 | 0,00687 |
| 172,51446 | 0,00692 |
| 172,96877 | 0,00698 |
| 173,42308 | 0,00703 |
| 173,87738 | 0,00709 |
| 174,33169 | 0,00714 |
| 174,78599 | 0,00719 |
| 175,2403 | 0,00724 |
| 175,69461 | 0,0073 |
| 176,14891 | 0,00735 |
| 176,60322 | 0,0074 |
| 177,05753 | 0,00744 |
| 177,51183 | 0,00749 |
| 177,96614 | 0,00754 |
| 178,42045 | 0,00758 |
| 178,87475 | 0,00763 |
| 179,32906 | 0,00767 |
| 179,78337 | 0,00772 |
| 180,23767 | 0,00776 |
| 180,69198 | 0,0078 |
| 181,14628 | 0,00784 |
| 181,60059 | 0,00788 |
| 182,0549 | 0,00792 |
| 182,5092 | 0,00796 |
| 182,96351 | 0,00799 |
| 183,41782 | 0,00803 |
| 183,87212 | 0,00806 |
| 184,32643 | 0,0081 |
| 184,78074 | 0,00813 |
| 185,23504 | 0,00816 |
| 185,68935 | 0,00819 |
| 186,14365 | 0,00822 |
| 186,59796 | 0,00825 |
| 187,05227 | 0,00828 |
| 187,50657 | 0,00831 |
| 187,96088 | 0,00833 |
| 188,41519 | 0,00835 |
| 188,86949 | 0,00838 |
| 189,3238 | 0,0084 |
| 189,77811 | 0,00842 |
| 190,23241 | 0,00844 |
| 190,68672 | 0,00846 |
| 191,14103 | 0,00847 |
| 191,59533 | 0,00849 |
| 192,04964 | 0,00851 |
| 192,50394 | 0,00852 |
| 192,95825 | 0,00853 |
| 193,41256 | 0,00855 |
| 193,86686 | 0,00856 |
| 194,32117 | 0,00857 |
| 194,77548 | 0,00858 |
| 195,22978 | 0,0086 |
| 195,68409 | 0,00861 |
| 196,1384 | 0,00862 |
| 196,5927 | 0,00863 |
| 197,04701 | 0,00864 |
| 197,50131 | 0,00865 |
| 197,95562 | 0,00866 |
| 198,40993 | 0,00867 |
| 198,86423 | 0,00868 |
| 199,31854 | 0,00869 |
| 199,77285 | 0,0087 |
| 200,22715 | 0,00871 |
| 200,68146 | 0,00872 |
| 201,13577 | 0,00873 |
| 201,59007 | 0,00874 |
| 202,04438 | 0,00875 |
| 202,49869 | 0,00875 |
| 202,95299 | 0,00876 |
| 203,4073 | 0,00877 |
| 203,8616 | 0,00877 |
| 204,31591 | 0,00878 |
| 204,77022 | 0,00878 |
| 205,22452 | 0,00878 |
| 205,67883 | 0,00878 |
| 206,13314 | 0,00878 |
| 206,58744 | 0,00878 |
| 207,04175 | 0,00878 |
| 207,49606 | 0,00878 |
| 207,95036 | 0,00878 |
| 208,40467 | 0,00878 |
| 208,85897 | 0,00877 |
| 209,31328 | 0,00877 |
| 209,76759 | 0,00876 |
| 210,22189 | 0,00875 |
| 210,6762 | 0,00875 |
| 211,13051 | 0,00874 |
| 211,58481 | 0,00872 |
| 212,03912 | 0,00871 |
| 212,49343 | 0,0087 |
| 212,94773 | 0,00868 |
| 213,40204 | 0,00866 |
| 213,85635 | 0,00864 |
| 214,31065 | 0,00861 |
| 214,76496 | 0,00859 |
| 215,21926 | 0,00856 |
| 215,67357 | 0,00852 |
| 216,12788 | 0,00849 |
| 216,58218 | 0,00845 |
| 217,03649 | 0,00841 |
| 217,4908 | 0,00837 |
| 217,9451 | 0,00832 |
| 218,39941 | 0,00828 |
| 218,85372 | 0,00823 |
| 219,30802 | 0,00818 |
| 219,76233 | 0,00813 |
| 220,21663 | 0,00808 |
| 220,67094 | 0,00802 |
| 221,12525 | 0,00797 |
| 221,57955 | 0,00792 |
| 222,03386 | 0,00786 |
| 222,48817 | 0,00781 |
| 222,94247 | 0,00776 |
| 223,39678 | 0,0077 |
| 223,85109 | 0,00765 |
| 224,30539 | 0,0076 |
| 224,7597 | 0,00754 |
| 225,21401 | 0,00749 |
| 225,66831 | 0,00744 |
| 226,12262 | 0,00739 |
| 226,57692 | 0,00734 |
| 227,03123 | 0,00728 |
| 227,48554 | 0,00723 |
| 227,93984 | 0,00718 |
| 228,39415 | 0,00713 |
| 228,84846 | 0,00707 |
| 229,30276 | 0,00702 |
| 229,75707 | 0,00696 |
| 230,21138 | 0,00691 |
| 230,66568 | 0,00685 |
| 231,11999 | 0,00679 |
| 231,57429 | 0,00673 |
| 232,0286 | 0,00667 |
| 232,48291 | 0,00661 |
| 232,93721 | 0,00655 |
| 233,39152 | 0,00648 |
| 233,84583 | 0,00642 |
| 234,30013 | 0,00635 |
| 234,75444 | 0,00629 |
| 235,20875 | 0,00622 |
| 235,66305 | 0,00615 |
| 236,11736 | 0,00608 |
| 236,57167 | 0,00601 |
| 237,02597 | 0,00594 |
| 237,48028 | 0,00586 |
| 237,93458 | 0,00579 |
| 238,38889 | 0,00572 |
| 238,8432 | 0,00564 |
| 239,2975 | 0,00557 |
| 239,75181 | 0,0055 |
| 240,20612 | 0,00542 |
| 240,66042 | 0,00535 |
| 241,11473 | 0,00527 |
| 241,56904 | 0,00519 |
| 242,02334 | 0,00512 |
| 242,47765 | 0,00504 |
| 242,93196 | 0,00497 |
| 243,38626 | 0,00489 |
| 243,84057 | 0,00482 |
| 244,29487 | 0,00474 |
| 244,74918 | 0,00467 |
| 245,20349 | 0,0046 |
| 245,65779 | 0,00453 |
| 246,1121 | 0,00446 |
| 246,56641 | 0,00439 |
| 247,02071 | 0,00432 |
| 247,47502 | 0,00425 |
| 247,92933 | 0,00418 |
| 248,38363 | 0,00412 |
| 248,83794 | 0,00406 |
| 249,29224 | 0,004 |
| 249,74655 | 0,00394 |
| 250,20086 | 0,00388 |
| 250,65516 | 0,00382 |
| 251,10947 | 0,00376 |
| 251,56378 | 0,00371 |
| 252,01808 | 0,00365 |
| 252,47239 | 0,0036 |
| 252,9267 | 0,00354 |
| 253,381 | 0,00349 |
| 253,83531 | 0,00344 |
| 254,28962 | 0,00338 |
| 254,74392 | 0,00333 |
| 255,19823 | 0,00327 |
| 255,65253 | 0,00322 |
| 256,10684 | 0,00317 |
| 256,56115 | 0,00311 |
| 257,01545 | 0,00306 |
| 257,46976 | 0,003 |
| 257,92407 | 0,00295 |
| 258,37837 | 0,00289 |
| 258,83268 | 0,00284 |
| 259,28699 | 0,00278 |
| 259,74129 | 0,00273 |
| 260,1956 | 0,00267 |
| 260,6499 | 0,00262 |
| 261,10421 | 0,00257 |
| 261,55852 | 0,00251 |
| 262,01282 | 0,00246 |
| 262,46713 | 0,00241 |
| 262,92144 | 0,00236 |
| 263,37574 | 0,00231 |
| 263,83005 | 0,00226 |
| 264,28436 | 0,00222 |
| 264,73866 | 0,00217 |
| 265,19297 | 0,00212 |
| 265,64728 | 0,00208 |
| 266,10158 | 0,00204 |
| 266,55589 | 0,00199 |
| 267,01019 | 0,00195 |
| 267,4645 | 0,00191 |
| 267,91881 | 0,00187 |
| 268,37311 | 0,00183 |
| 268,82742 | 0,00179 |
| 269,28173 | 0,00176 |
| 269,73603 | 0,00172 |
| 270,19034 | 0,00168 |
| 270,64465 | 0,00164 |
| 271,09895 | 0,00161 |
| 271,55326 | 0,00157 |
| 272,00756 | 0,00154 |
| 272,46187 | 0,0015 |
| 272,91618 | 0,00147 |
| 273,37048 | 0,00143 |
| 273,82479 | 0,0014 |
| 274,2791 | 0,00137 |
| 274,7334 | 0,00134 |
| 275,18771 | 0,00131 |
| 275,64202 | 0,00128 |
| 276,09632 | 0,00125 |
| 276,55063 | 0,00122 |
| 277,00494 | 0,00119 |
| 277,45924 | 0,00117 |
| 277,91355 | 0,00114 |
| 278,36785 | 0,00112 |
| 278,82216 | 0,0011 |
| 279,27647 | 0,00107 |
| 279,73077 | 0,00105 |
| 280,18508 | 0,00103 |
| 280,63939 | 0,00101 |
| 281,09369 | 0,00099 |
| 281,548 | 0,00097 |
| 282,00231 | 0,00095 |
| 282,45661 | 0,00093 |
| 282,91092 | 0,00091 |
| 283,36522 | 0,00089 |
| 283,81953 | 0,00088 |
| 284,27384 | 0,00086 |
| 284,72814 | 0,00084 |
| 285,18245 | 0,00083 |
| 285,63676 | 0,00081 |
| 286,09106 | 0,0008 |
| 286,54537 | 0,00078 |
| 286,99968 | 0,00077 |
| 287,45398 | 0,00075 |
| 287,90829 | 0,00074 |
| 288,3626 | 0,00073 |
| 288,8169 | 0,00072 |
| 289,27121 | 0,0007 |
| 289,72551 | 0,00069 |
| 290,17982 | 0,00068 |
| 290,63413 | 0,00068 |
| 291,08843 | 0,00067 |
| 291,54274 | 0,00066 |
| 291,99705 | 0,00065 |
| 292,45135 | 0,00065 |
| 292,90566 | 0,00064 |
| 293,35997 | 0,00064 |
| 293,81427 | 0,00063 |
| 294,26858 | 0,00063 |
| 294,72288 | 0,00062 |
| 295,17719 | 0,00062 |
| 295,6315 | 0,00061 |
| 296,0858 | 0,00061 |
| 296,54011 | 0,0006 |
| 296,99442 | 0,00059 |
| 297,44872 | 0,00058 |
| 297,90303 | 0,00058 |
| 298,35734 | 0,00056 |
| 298,81164 | 0,00055 |
| 299,26595 | 0,00054 |
| 300 | 0,00052 |
| Eindtoetsscore | Dichtheid (Dichtheid) |
|---|---|
| 321 | 0,00049 |
| 321,21235 | 0,0005 |
| 321,36715 | 0,00051 |
| 321,52195 | 0,00052 |
| 321,67674 | 0,00053 |
| 321,83154 | 0,00054 |
| 321,98634 | 0,00055 |
| 322,14114 | 0,00055 |
| 322,29593 | 0,00056 |
| 322,45073 | 0,00057 |
| 322,60553 | 0,00058 |
| 322,76033 | 0,00058 |
| 322,91512 | 0,00059 |
| 323,06992 | 0,0006 |
| 323,22472 | 0,00061 |
| 323,37952 | 0,00063 |
| 323,53431 | 0,00064 |
| 323,68911 | 0,00065 |
| 323,84391 | 0,00067 |
| 323,99871 | 0,00068 |
| 324,1535 | 0,0007 |
| 324,3083 | 0,00071 |
| 324,4631 | 0,00073 |
| 324,6179 | 0,00074 |
| 324,77269 | 0,00075 |
| 324,92749 | 0,00077 |
| 325,08229 | 0,00078 |
| 325,23709 | 0,00079 |
| 325,39188 | 0,0008 |
| 325,54668 | 0,00081 |
| 325,70148 | 0,00082 |
| 325,85628 | 0,00083 |
| 326,01107 | 0,00084 |
| 326,16587 | 0,00085 |
| 326,32067 | 0,00086 |
| 326,47547 | 0,00087 |
| 326,63026 | 0,00088 |
| 326,78506 | 0,0009 |
| 326,93986 | 0,00092 |
| 327,09466 | 0,00094 |
| 327,24945 | 0,00096 |
| 327,40425 | 0,00098 |
| 327,55905 | 0,00101 |
| 327,71385 | 0,00105 |
| 327,86864 | 0,00108 |
| 328,02344 | 0,00112 |
| 328,17824 | 0,00117 |
| 328,33304 | 0,00121 |
| 328,48783 | 0,00126 |
| 328,64263 | 0,00131 |
| 328,79743 | 0,00137 |
| 328,95223 | 0,00143 |
| 329,10702 | 0,00149 |
| 329,26182 | 0,00155 |
| 329,41662 | 0,00162 |
| 329,57142 | 0,00168 |
| 329,72621 | 0,00175 |
| 329,88101 | 0,00182 |
| 330,03581 | 0,00188 |
| 330,19061 | 0,00195 |
| 330,3454 | 0,00202 |
| 330,5002 | 0,00209 |
| 330,655 | 0,00216 |
| 330,8098 | 0,00223 |
| 330,96459 | 0,0023 |
| 331,11939 | 0,00237 |
| 331,27419 | 0,00243 |
| 331,42899 | 0,0025 |
| 331,58378 | 0,00258 |
| 331,73858 | 0,00265 |
| 331,89338 | 0,00272 |
| 332,04818 | 0,00279 |
| 332,20297 | 0,00287 |
| 332,35777 | 0,00294 |
| 332,51257 | 0,00302 |
| 332,66737 | 0,0031 |
| 332,82216 | 0,00318 |
| 332,97696 | 0,00327 |
| 333,13176 | 0,00336 |
| 333,28656 | 0,00344 |
| 333,44135 | 0,00354 |
| 333,59615 | 0,00363 |
| 333,75095 | 0,00373 |
| 333,90575 | 0,00383 |
| 334,06054 | 0,00393 |
| 334,21534 | 0,00403 |
| 334,37014 | 0,00413 |
| 334,52494 | 0,00424 |
| 334,67973 | 0,00435 |
| 334,83453 | 0,00446 |
| 334,98933 | 0,00456 |
| 335,14413 | 0,00467 |
| 335,29892 | 0,00478 |
| 335,45372 | 0,00489 |
| 335,60852 | 0,005 |
| 335,76332 | 0,00511 |
| 335,91811 | 0,00521 |
| 336,07291 | 0,00532 |
| 336,22771 | 0,00542 |
| 336,38251 | 0,00553 |
| 336,5373 | 0,00563 |
| 336,6921 | 0,00574 |
| 336,8469 | 0,00584 |
| 337,0017 | 0,00595 |
| 337,15649 | 0,00605 |
| 337,31129 | 0,00616 |
| 337,46609 | 0,00627 |
| 337,62089 | 0,00638 |
| 337,77568 | 0,00649 |
| 337,93048 | 0,00661 |
| 338,08528 | 0,00673 |
| 338,24008 | 0,00686 |
| 338,39487 | 0,00698 |
| 338,54967 | 0,00712 |
| 338,70447 | 0,00725 |
| 338,85927 | 0,0074 |
| 339,01406 | 0,00754 |
| 339,16886 | 0,00769 |
| 339,32366 | 0,00784 |
| 339,47846 | 0,008 |
| 339,63325 | 0,00816 |
| 339,78805 | 0,00833 |
| 339,94285 | 0,00849 |
| 340,09765 | 0,00866 |
| 340,25244 | 0,00884 |
| 340,40724 | 0,00901 |
| 340,56204 | 0,00919 |
| 340,71684 | 0,00936 |
| 340,87163 | 0,00954 |
| 341,02643 | 0,00972 |
| 341,18123 | 0,0099 |
| 341,33603 | 0,01008 |
| 341,49082 | 0,01026 |
| 341,64562 | 0,01044 |
| 341,80042 | 0,01062 |
| 341,95522 | 0,0108 |
| 342,11001 | 0,01098 |
| 342,26481 | 0,01116 |
| 342,41961 | 0,01133 |
| 342,57441 | 0,01151 |
| 342,7292 | 0,01169 |
| 342,884 | 0,01187 |
| 343,0388 | 0,01205 |
| 343,1936 | 0,01224 |
| 343,3484 | 0,01242 |
| 343,50319 | 0,0126 |
| 343,65799 | 0,01279 |
| 343,81279 | 0,01298 |
| 343,96759 | 0,01317 |
| 344,12238 | 0,01336 |
| 344,27718 | 0,01356 |
| 344,43198 | 0,01376 |
| 344,58678 | 0,01396 |
| 344,74157 | 0,01416 |
| 344,89637 | 0,01437 |
| 345,05117 | 0,01458 |
| 345,20597 | 0,01479 |
| 345,36076 | 0,01501 |
| 345,51556 | 0,01522 |
| 345,67036 | 0,01545 |
| 345,82516 | 0,01567 |
| 345,97995 | 0,0159 |
| 346,13475 | 0,01613 |
| 346,28955 | 0,01637 |
| 346,44435 | 0,01661 |
| 346,59914 | 0,01686 |
| 346,75394 | 0,01711 |
| 346,90874 | 0,01736 |
| 347,06354 | 0,01762 |
| 347,21833 | 0,01789 |
| 347,37313 | 0,01815 |
| 347,52793 | 0,01842 |
| 347,68273 | 0,0187 |
| 347,83752 | 0,01897 |
| 347,99232 | 0,01925 |
| 348,14712 | 0,01952 |
| 348,30192 | 0,0198 |
| 348,45671 | 0,02008 |
| 348,61151 | 0,02036 |
| 348,76631 | 0,02063 |
| 348,92111 | 0,0209 |
| 349,0759 | 0,02117 |
| 349,2307 | 0,02144 |
| 349,3855 | 0,02171 |
| 349,5403 | 0,02198 |
| 349,69509 | 0,02224 |
| 349,84989 | 0,02251 |
| 350,00469 | 0,02277 |
| 350,15949 | 0,02304 |
| 350,31428 | 0,0233 |
| 350,46908 | 0,02357 |
| 350,62388 | 0,02383 |
| 350,77868 | 0,0241 |
| 350,93347 | 0,02437 |
| 351,08827 | 0,02464 |
| 351,24307 | 0,02492 |
| 351,39787 | 0,02519 |
| 351,55266 | 0,02547 |
| 351,70746 | 0,02575 |
| 351,86226 | 0,02602 |
| 352,01706 | 0,0263 |
| 352,17185 | 0,02658 |
| 352,32665 | 0,02686 |
| 352,48145 | 0,02714 |
| 352,63625 | 0,02742 |
| 352,79104 | 0,02769 |
| 352,94584 | 0,02796 |
| 353,10064 | 0,02823 |
| 353,25544 | 0,02849 |
| 353,41023 | 0,02875 |
| 353,56503 | 0,029 |
| 353,71983 | 0,02924 |
| 353,87463 | 0,02948 |
| 354,02942 | 0,0297 |
| 354,18422 | 0,02992 |
| 354,33902 | 0,03013 |
| 354,49382 | 0,03032 |
| 354,64861 | 0,0305 |
| 354,80341 | 0,03067 |
| 354,95821 | 0,03083 |
| 355,11301 | 0,03098 |
| 355,2678 | 0,03111 |
| 355,4226 | 0,03123 |
| 355,5774 | 0,03133 |
| 355,7322 | 0,03143 |
| 355,88699 | 0,03151 |
| 356,04179 | 0,03158 |
| 356,19659 | 0,03164 |
| 356,35139 | 0,0317 |
| 356,50618 | 0,03174 |
| 356,66098 | 0,03179 |
| 356,81578 | 0,03182 |
| 356,97058 | 0,03186 |
| 357,12537 | 0,03189 |
| 357,28017 | 0,03192 |
| 357,43497 | 0,03196 |
| 357,58977 | 0,032 |
| 357,74456 | 0,03204 |
| 357,89936 | 0,03209 |
| 358,05416 | 0,03214 |
| 358,20896 | 0,0322 |
| 358,36375 | 0,03227 |
| 358,51855 | 0,03235 |
| 358,67335 | 0,03243 |
| 358,82815 | 0,03253 |
| 358,98294 | 0,03263 |
| 359,13774 | 0,03274 |
| 359,29254 | 0,03285 |
| 359,44734 | 0,03297 |
| 359,60213 | 0,0331 |
| 359,75693 | 0,03322 |
| 359,91173 | 0,03335 |
| 360,06653 | 0,03347 |
| 360,22132 | 0,0336 |
| 360,37612 | 0,03371 |
| 360,53092 | 0,03382 |
| 360,68572 | 0,03393 |
| 360,84051 | 0,03402 |
| 360,99531 | 0,03411 |
| 361,15011 | 0,03418 |
| 361,30491 | 0,03424 |
| 361,4597 | 0,03429 |
| 361,6145 | 0,03432 |
| 361,7693 | 0,03434 |
| 361,9241 | 0,03435 |
| 362,07889 | 0,03434 |
| 362,23369 | 0,03431 |
| 362,38849 | 0,03428 |
| 362,54329 | 0,03423 |
| 362,69808 | 0,03417 |
| 362,85288 | 0,0341 |
| 363,00768 | 0,03401 |
| 363,16248 | 0,03392 |
| 363,31727 | 0,03382 |
| 363,47207 | 0,03371 |
| 363,62687 | 0,03359 |
| 363,78167 | 0,03346 |
| 363,93646 | 0,03333 |
| 364,09126 | 0,03319 |
| 364,24606 | 0,03305 |
| 364,40086 | 0,0329 |
| 364,55565 | 0,03274 |
| 364,71045 | 0,03258 |
| 364,86525 | 0,03242 |
| 365,02005 | 0,03224 |
| 365,17484 | 0,03206 |
| 365,32964 | 0,03188 |
| 365,48444 | 0,03168 |
| 365,63924 | 0,03148 |
| 365,79403 | 0,03127 |
| 365,94883 | 0,03105 |
| 366,10363 | 0,03083 |
| 366,25843 | 0,03059 |
| 366,41322 | 0,03034 |
| 366,56802 | 0,03009 |
| 366,72282 | 0,02983 |
| 366,87762 | 0,02956 |
| 367,03241 | 0,02929 |
| 367,18721 | 0,029 |
| 367,34201 | 0,02872 |
| 367,49681 | 0,02843 |
| 367,6516 | 0,02813 |
| 367,8064 | 0,02784 |
| 367,9612 | 0,02754 |
| 368,116 | 0,02725 |
| 368,2708 | 0,02696 |
| 368,42559 | 0,02667 |
| 368,58039 | 0,02638 |
| 368,73519 | 0,02609 |
| 368,88999 | 0,02581 |
| 369,04478 | 0,02553 |
| 369,19958 | 0,02525 |
| 369,35438 | 0,02497 |
| 369,50918 | 0,0247 |
| 369,66397 | 0,02442 |
| 369,81877 | 0,02414 |
| 369,97357 | 0,02386 |
| 370,12837 | 0,02358 |
| 370,28316 | 0,02329 |
| 370,43796 | 0,023 |
| 370,59276 | 0,0227 |
| 370,74756 | 0,0224 |
| 370,90235 | 0,0221 |
| 371,05715 | 0,02179 |
| 371,21195 | 0,02147 |
| 371,36675 | 0,02115 |
| 371,52154 | 0,02082 |
| 371,67634 | 0,02048 |
| 371,83114 | 0,02015 |
| 371,98594 | 0,01981 |
| 372,14073 | 0,01947 |
| 372,29553 | 0,01912 |
| 372,45033 | 0,01878 |
| 372,60513 | 0,01844 |
| 372,75992 | 0,01809 |
| 372,91472 | 0,01776 |
| 373,06952 | 0,01742 |
| 373,22432 | 0,01709 |
| 373,37911 | 0,01677 |
| 373,53391 | 0,01645 |
| 373,68871 | 0,01614 |
| 373,84351 | 0,01584 |
| 373,9983 | 0,01555 |
| 374,1531 | 0,01526 |
| 374,3079 | 0,01499 |
| 374,4627 | 0,01472 |
| 374,61749 | 0,01446 |
| 374,77229 | 0,01421 |
| 374,92709 | 0,01397 |
| 375,08189 | 0,01373 |
| 375,23668 | 0,0135 |
| 375,39148 | 0,01327 |
| 375,54628 | 0,01306 |
| 375,70108 | 0,01284 |
| 375,85587 | 0,01263 |
| 376,01067 | 0,01243 |
| 376,16547 | 0,01223 |
| 376,32027 | 0,01203 |
| 376,47506 | 0,01183 |
| 376,62986 | 0,01164 |
| 376,78466 | 0,01145 |
| 376,93946 | 0,01126 |
| 377,09425 | 0,01108 |
| 377,24905 | 0,0109 |
| 377,40385 | 0,01072 |
| 377,55865 | 0,01054 |
| 377,71344 | 0,01036 |
| 377,86824 | 0,01019 |
| 378,02304 | 0,01001 |
| 378,17784 | 0,00984 |
| 378,33263 | 0,00967 |
| 378,48743 | 0,0095 |
| 378,64223 | 0,00933 |
| 378,79703 | 0,00916 |
| 378,95182 | 0,00899 |
| 379,10662 | 0,00882 |
| 379,26142 | 0,00865 |
| 379,41622 | 0,00848 |
| 379,57101 | 0,0083 |
| 379,72581 | 0,00813 |
| 379,88061 | 0,00796 |
| 380,03541 | 0,00779 |
| 380,1902 | 0,00761 |
| 380,345 | 0,00744 |
| 380,4998 | 0,00726 |
| 380,6546 | 0,00709 |
| 380,80939 | 0,00692 |
| 380,96419 | 0,00675 |
| 381,11899 | 0,00658 |
| 381,27379 | 0,00641 |
| 381,42858 | 0,00625 |
| 381,58338 | 0,00609 |
| 381,73818 | 0,00593 |
| 381,89298 | 0,00578 |
| 382,04777 | 0,00563 |
| 382,20257 | 0,00548 |
| 382,35737 | 0,00534 |
| 382,51217 | 0,0052 |
| 382,66696 | 0,00506 |
| 382,82176 | 0,00493 |
| 382,97656 | 0,0048 |
| 383,13136 | 0,00467 |
| 383,28615 | 0,00454 |
| 383,44095 | 0,00441 |
| 383,59575 | 0,00429 |
| 383,75055 | 0,00417 |
| 383,90534 | 0,00405 |
| 384,06014 | 0,00393 |
| 384,21494 | 0,00381 |
| 384,36974 | 0,0037 |
| 384,52453 | 0,00359 |
| 384,67933 | 0,00348 |
| 384,83413 | 0,00337 |
| 384,98893 | 0,00326 |
| 385,14372 | 0,00316 |
| 385,29852 | 0,00306 |
| 385,45332 | 0,00297 |
| 385,60812 | 0,00288 |
| 385,76291 | 0,0028 |
| 385,91771 | 0,00272 |
| 386,07251 | 0,00265 |
| 386,22731 | 0,00259 |
| 386,3821 | 0,00253 |
| 386,5369 | 0,00248 |
| 386,6917 | 0,00244 |
| 386,8465 | 0,0024 |
| 387,00129 | 0,00237 |
| 387,15609 | 0,00234 |
| 387,31089 | 0,00232 |
| 387,46569 | 0,0023 |
| 387,62048 | 0,00229 |
| 387,77528 | 0,00228 |
| 387,93008 | 0,00228 |
| 388,08488 | 0,00227 |
| 388,23967 | 0,00226 |
| 388,39447 | 0,00226 |
| 388,54927 | 0,00225 |
| 388,70407 | 0,00224 |
| 388,85886 | 0,00222 |
| 389,01366 | 0,0022 |
| 389,16846 | 0,00217 |
| 389,32326 | 0,00214 |
| 389,47805 | 0,0021 |
| 389,63285 | 0,00205 |
| 389,78765 | 0,00199 |
| 390 | 0,00193 |
| Eindtoetsscore | Dichtheid (Dichtheid) |
|---|---|
| 300 | 0,00568 |
| 300,77567 | 0,00583 |
| 301,29112 | 0,00597 |
| 301,80657 | 0,00611 |
| 302,32202 | 0,00624 |
| 302,83748 | 0,00636 |
| 303,35293 | 0,00648 |
| 303,86838 | 0,00659 |
| 304,38383 | 0,00669 |
| 304,89928 | 0,00679 |
| 305,41473 | 0,00687 |
| 305,93018 | 0,00695 |
| 306,44563 | 0,00702 |
| 306,96108 | 0,00708 |
| 307,47653 | 0,00713 |
| 307,99199 | 0,00718 |
| 308,50744 | 0,00722 |
| 309,02289 | 0,00725 |
| 309,53834 | 0,00727 |
| 310,05379 | 0,00728 |
| 310,56924 | 0,00729 |
| 311,08469 | 0,00729 |
| 311,60014 | 0,00729 |
| 312,11559 | 0,00727 |
| 312,63105 | 0,00726 |
| 313,1465 | 0,00723 |
| 313,66195 | 0,0072 |
| 314,1774 | 0,00717 |
| 314,69285 | 0,00713 |
| 315,2083 | 0,00709 |
| 315,72375 | 0,00705 |
| 316,2392 | 0,007 |
| 316,75465 | 0,00694 |
| 317,2701 | 0,00689 |
| 317,78556 | 0,00683 |
| 318,30101 | 0,00678 |
| 318,81646 | 0,00672 |
| 319,33191 | 0,00665 |
| 319,84736 | 0,00659 |
| 320,36281 | 0,00653 |
| 320,87826 | 0,00647 |
| 321,39371 | 0,0064 |
| 321,90916 | 0,00634 |
| 322,42462 | 0,00628 |
| 322,94007 | 0,00621 |
| 323,45552 | 0,00615 |
| 323,97097 | 0,00609 |
| 324,48642 | 0,00603 |
| 325,00187 | 0,00597 |
| 325,51732 | 0,00592 |
| 326,03277 | 0,00586 |
| 326,54822 | 0,00581 |
| 327,06367 | 0,00576 |
| 327,57913 | 0,00571 |
| 328,09458 | 0,00566 |
| 328,61003 | 0,00561 |
| 329,12548 | 0,00556 |
| 329,64093 | 0,00552 |
| 330,15638 | 0,00548 |
| 330,67183 | 0,00544 |
| 331,18728 | 0,0054 |
| 331,70273 | 0,00537 |
| 332,21819 | 0,00533 |
| 332,73364 | 0,0053 |
| 333,24909 | 0,00527 |
| 333,76454 | 0,00524 |
| 334,27999 | 0,00521 |
| 334,79544 | 0,00518 |
| 335,31089 | 0,00516 |
| 335,82634 | 0,00514 |
| 336,34179 | 0,00512 |
| 336,85725 | 0,0051 |
| 337,3727 | 0,00508 |
| 337,88815 | 0,00506 |
| 338,4036 | 0,00504 |
| 338,91905 | 0,00503 |
| 339,4345 | 0,00501 |
| 339,94995 | 0,005 |
| 340,4654 | 0,00498 |
| 340,98085 | 0,00497 |
| 341,4963 | 0,00496 |
| 342,01176 | 0,00495 |
| 342,52721 | 0,00494 |
| 343,04266 | 0,00493 |
| 343,55811 | 0,00492 |
| 344,07356 | 0,00491 |
| 344,58901 | 0,0049 |
| 345,10446 | 0,00489 |
| 345,61991 | 0,00488 |
| 346,13536 | 0,00488 |
| 346,65082 | 0,00487 |
| 347,16627 | 0,00486 |
| 347,68172 | 0,00485 |
| 348,19717 | 0,00485 |
| 348,71262 | 0,00484 |
| 349,22807 | 0,00483 |
| 349,74352 | 0,00482 |
| 350,25897 | 0,00482 |
| 350,77442 | 0,00481 |
| 351,28987 | 0,0048 |
| 351,80533 | 0,00479 |
| 352,32078 | 0,00479 |
| 352,83623 | 0,00478 |
| 353,35168 | 0,00477 |
| 353,86713 | 0,00476 |
| 354,38258 | 0,00475 |
| 354,89803 | 0,00474 |
| 355,41348 | 0,00474 |
| 355,92893 | 0,00473 |
| 356,44439 | 0,00472 |
| 356,95984 | 0,00471 |
| 357,47529 | 0,0047 |
| 357,99074 | 0,00469 |
| 358,50619 | 0,00468 |
| 359,02164 | 0,00467 |
| 359,53709 | 0,00466 |
| 360,05254 | 0,00465 |
| 360,56799 | 0,00464 |
| 361,08344 | 0,00463 |
| 361,5989 | 0,00461 |
| 362,11435 | 0,0046 |
| 362,6298 | 0,00459 |
| 363,14525 | 0,00458 |
| 363,6607 | 0,00457 |
| 364,17615 | 0,00456 |
| 364,6916 | 0,00455 |
| 365,20705 | 0,00454 |
| 365,7225 | 0,00453 |
| 366,23796 | 0,00452 |
| 366,75341 | 0,0045 |
| 367,26886 | 0,00449 |
| 367,78431 | 0,00448 |
| 368,29976 | 0,00447 |
| 368,81521 | 0,00446 |
| 369,33066 | 0,00446 |
| 369,84611 | 0,00445 |
| 370,36156 | 0,00444 |
| 370,87702 | 0,00443 |
| 371,39247 | 0,00442 |
| 371,90792 | 0,00441 |
| 372,42337 | 0,00441 |
| 372,93882 | 0,0044 |
| 373,45427 | 0,00439 |
| 373,96972 | 0,00439 |
| 374,48517 | 0,00438 |
| 375,00062 | 0,00438 |
| 375,51607 | 0,00437 |
| 376,03153 | 0,00437 |
| 376,54698 | 0,00437 |
| 377,06243 | 0,00436 |
| 377,57788 | 0,00436 |
| 378,09333 | 0,00436 |
| 378,60878 | 0,00436 |
| 379,12423 | 0,00435 |
| 379,63968 | 0,00435 |
| 380,15513 | 0,00435 |
| 380,67059 | 0,00435 |
| 381,18604 | 0,00435 |
| 381,70149 | 0,00435 |
| 382,21694 | 0,00435 |
| 382,73239 | 0,00435 |
| 383,24784 | 0,00435 |
| 383,76329 | 0,00435 |
| 384,27874 | 0,00435 |
| 384,79419 | 0,00435 |
| 385,30964 | 0,00435 |
| 385,8251 | 0,00436 |
| 386,34055 | 0,00436 |
| 386,856 | 0,00436 |
| 387,37145 | 0,00436 |
| 387,8869 | 0,00436 |
| 388,40235 | 0,00436 |
| 388,9178 | 0,00436 |
| 389,43325 | 0,00436 |
| 389,9487 | 0,00437 |
| 390,46416 | 0,00437 |
| 390,97961 | 0,00437 |
| 391,49506 | 0,00437 |
| 392,01051 | 0,00437 |
| 392,52596 | 0,00437 |
| 393,04141 | 0,00437 |
| 393,55686 | 0,00437 |
| 394,07231 | 0,00437 |
| 394,58776 | 0,00437 |
| 395,10321 | 0,00438 |
| 395,61867 | 0,00438 |
| 396,13412 | 0,00438 |
| 396,64957 | 0,00438 |
| 397,16502 | 0,00438 |
| 397,68047 | 0,00438 |
| 398,19592 | 0,00438 |
| 398,71137 | 0,00438 |
| 399,22682 | 0,00438 |
| 399,74227 | 0,00438 |
| 400,25773 | 0,00438 |
| 400,77318 | 0,00438 |
| 401,28863 | 0,00438 |
| 401,80408 | 0,00438 |
| 402,31953 | 0,00438 |
| 402,83498 | 0,00438 |
| 403,35043 | 0,00438 |
| 403,86588 | 0,00437 |
| 404,38133 | 0,00437 |
| 404,89679 | 0,00437 |
| 405,41224 | 0,00437 |
| 405,92769 | 0,00437 |
| 406,44314 | 0,00437 |
| 406,95859 | 0,00437 |
| 407,47404 | 0,00437 |
| 407,98949 | 0,00436 |
| 408,50494 | 0,00436 |
| 409,02039 | 0,00436 |
| 409,53584 | 0,00436 |
| 410,0513 | 0,00436 |
| 410,56675 | 0,00435 |
| 411,0822 | 0,00435 |
| 411,59765 | 0,00435 |
| 412,1131 | 0,00435 |
| 412,62855 | 0,00434 |
| 413,144 | 0,00434 |
| 413,65945 | 0,00434 |
| 414,1749 | 0,00433 |
| 414,69036 | 0,00433 |
| 415,20581 | 0,00433 |
| 415,72126 | 0,00432 |
| 416,23671 | 0,00432 |
| 416,75216 | 0,00431 |
| 417,26761 | 0,00431 |
| 417,78306 | 0,0043 |
| 418,29851 | 0,0043 |
| 418,81396 | 0,00429 |
| 419,32941 | 0,00429 |
| 419,84487 | 0,00429 |
| 420,36032 | 0,00428 |
| 420,87577 | 0,00428 |
| 421,39122 | 0,00427 |
| 421,90667 | 0,00426 |
| 422,42212 | 0,00426 |
| 422,93757 | 0,00425 |
| 423,45302 | 0,00425 |
| 423,96847 | 0,00424 |
| 424,48393 | 0,00424 |
| 424,99938 | 0,00423 |
| 425,51483 | 0,00423 |
| 426,03028 | 0,00423 |
| 426,54573 | 0,00422 |
| 427,06118 | 0,00422 |
| 427,57663 | 0,00421 |
| 428,09208 | 0,00421 |
| 428,60753 | 0,0042 |
| 429,12298 | 0,0042 |
| 429,63844 | 0,0042 |
| 430,15389 | 0,0042 |
| 430,66934 | 0,00419 |
| 431,18479 | 0,00419 |
| 431,70024 | 0,00419 |
| 432,21569 | 0,00419 |
| 432,73114 | 0,00419 |
| 433,24659 | 0,00419 |
| 433,76204 | 0,00419 |
| 434,2775 | 0,00419 |
| 434,79295 | 0,00419 |
| 435,3084 | 0,00419 |
| 435,82385 | 0,00419 |
| 436,3393 | 0,00419 |
| 436,85475 | 0,00419 |
| 437,3702 | 0,00419 |
| 437,88565 | 0,0042 |
| 438,4011 | 0,0042 |
| 438,91656 | 0,0042 |
| 439,43201 | 0,00421 |
| 439,94746 | 0,00421 |
| 440,46291 | 0,00421 |
| 440,97836 | 0,00422 |
| 441,49381 | 0,00422 |
| 442,00926 | 0,00422 |
| 442,52471 | 0,00423 |
| 443,04016 | 0,00423 |
| 443,55561 | 0,00423 |
| 444,07107 | 0,00424 |
| 444,58652 | 0,00424 |
| 445,10197 | 0,00424 |
| 445,61742 | 0,00425 |
| 446,13287 | 0,00425 |
| 446,64832 | 0,00425 |
| 447,16377 | 0,00426 |
| 447,67922 | 0,00426 |
| 448,19467 | 0,00426 |
| 448,71013 | 0,00426 |
| 449,22558 | 0,00426 |
| 449,74103 | 0,00426 |
| 450,25648 | 0,00426 |
| 450,77193 | 0,00426 |
| 451,28738 | 0,00426 |
| 451,80283 | 0,00426 |
| 452,31828 | 0,00426 |
| 452,83373 | 0,00426 |
| 453,34918 | 0,00426 |
| 453,86464 | 0,00425 |
| 454,38009 | 0,00425 |
| 454,89554 | 0,00425 |
| 455,41099 | 0,00424 |
| 455,92644 | 0,00424 |
| 456,44189 | 0,00424 |
| 456,95734 | 0,00423 |
| 457,47279 | 0,00423 |
| 457,98824 | 0,00422 |
| 458,5037 | 0,00422 |
| 459,01915 | 0,00422 |
| 459,5346 | 0,00421 |
| 460,05005 | 0,00421 |
| 460,5655 | 0,0042 |
| 461,08095 | 0,0042 |
| 461,5964 | 0,00419 |
| 462,11185 | 0,00419 |
| 462,6273 | 0,00418 |
| 463,14275 | 0,00418 |
| 463,65821 | 0,00417 |
| 464,17366 | 0,00417 |
| 464,68911 | 0,00417 |
| 465,20456 | 0,00416 |
| 465,72001 | 0,00416 |
| 466,23546 | 0,00416 |
| 466,75091 | 0,00415 |
| 467,26636 | 0,00415 |
| 467,78181 | 0,00415 |
| 468,29727 | 0,00415 |
| 468,81272 | 0,00414 |
| 469,32817 | 0,00414 |
| 469,84362 | 0,00414 |
| 470,35907 | 0,00414 |
| 470,87452 | 0,00414 |
| 471,38997 | 0,00414 |
| 471,90542 | 0,00414 |
| 472,42087 | 0,00414 |
| 472,93633 | 0,00413 |
| 473,45178 | 0,00413 |
| 473,96723 | 0,00413 |
| 474,48268 | 0,00413 |
| 474,99813 | 0,00413 |
| 475,51358 | 0,00413 |
| 476,02903 | 0,00412 |
| 476,54448 | 0,00412 |
| 477,05993 | 0,00412 |
| 477,57538 | 0,00411 |
| 478,09084 | 0,00411 |
| 478,60629 | 0,0041 |
| 479,12174 | 0,00409 |
| 479,63719 | 0,00408 |
| 480,15264 | 0,00407 |
| 480,66809 | 0,00406 |
| 481,18354 | 0,00405 |
| 481,69899 | 0,00404 |
| 482,21444 | 0,00402 |
| 482,7299 | 0,004 |
| 483,24535 | 0,00398 |
| 483,7608 | 0,00396 |
| 484,27625 | 0,00394 |
| 484,7917 | 0,00391 |
| 485,30715 | 0,00389 |
| 485,8226 | 0,00386 |
| 486,33805 | 0,00383 |
| 486,8535 | 0,00379 |
| 487,36895 | 0,00375 |
| 487,88441 | 0,00372 |
| 488,39986 | 0,00367 |
| 488,91531 | 0,00363 |
| 489,43076 | 0,00358 |
| 489,94621 | 0,00353 |
| 490,46166 | 0,00348 |
| 490,97711 | 0,00343 |
| 491,49256 | 0,00337 |
| 492,00801 | 0,00331 |
| 492,52347 | 0,00325 |
| 493,03892 | 0,00318 |
| 493,55437 | 0,00312 |
| 494,06982 | 0,00305 |
| 494,58527 | 0,00298 |
| 495,10072 | 0,00291 |
| 495,61617 | 0,00283 |
| 496,13162 | 0,00275 |
| 496,64707 | 0,00268 |
| 497,16252 | 0,0026 |
| 497,67798 | 0,00252 |
| 498,19343 | 0,00244 |
| 498,70888 | 0,00236 |
| 499,22433 | 0,00227 |
| 500 | 0,00219 |
De verschillende eindtoetsen laten een andere verdeling van de eindtoetsscores zien, die bij sommige aanbieders wel wat lijkt op een normale verdeling, maar bij met name AMN eerder lijkt op een uniforme verdeling.
Om toch te zien wat het effect is van een z-score, zullen we deze wel berekenen zodat we later bij de ontwikkeling van het herijkte model voor onderwijsachterstanden een vergelijking kunnen maken met een van de andere methoden. Dit doen we als volgt per toetsaanbieder t, met t = (AMN, CET, Dia, Iep, Route.8):
$$x_{herschaald\_ t} = \ \frac{x_{t} - \overline{x_{t}}}{\sigma(x_{t})}$$
Hierbij is xt de oorspronkelijke variabele met de eindtoetsscore per toetsaanbieder, (xt) het gemiddelde van de eindtoetsscores per toetsaanbieder en σ(xt) de standaarddeviatie van de eindtoetsscores per toetsaanbieder. Voor alle toetsaanbieders zal dan het gemiddelde 0 worden en de standaarddeviatie 1. Idealiter zouden we willen dat na standaardisatie de scores van de verschillende toetsaanbieders dicht bij elkaar liggen en nauwelijks te onderscheiden zijn.
Methode 2: Normalisatie met min-max transformatie naar toetsaanbieder en toetsadvies
Ten tweede passen we per toetsaanbieder een normalisatie met min-max transformatie toe waarbij we rekening houden met het bijbehorende toetsadvies. Over het algemeen kun je als volgt normaliseren met een min-max transformatie:
$$x_{herschaald} = \ \frac{x - \min(x)}{\max(x) - \min(x)}$$
Hierbij is x de oorspronkelijke variabele met de eindtoetsscore, min(x) het minimum van de variabele en max(x) het maximum van de variabele. Door het toepassen van deze formule valt de nieuwe variabele x in het bereik [0,1]. Om dit bereik aan te passen naar [a, b], kunnen we de formule als volgt gebruiken:
$$x_{herschaald} = a + \ \frac{\left( x - min(x) \right)*(b - a)}{max(x) - min(x)}$$
Omdat we rekening willen houden met zowel het toetsadvies als de toetsaanbieder, gaan we per combinatie van toetsadvies en toetsaanbieder normaliseren (per cel in tabel 5.2.1). Als we dit doen voor iedere cel apart, zal alles op een bereik van [0, 1] komen te liggen. Omdat we hierin ook de zes toetsadviezen willen meenemen, zullen we de schaal aanpassen per toetsadvies, zodat deze in totaal loopt van [0, 6]. Elk toetsadvies blijft hierbij een bereik van lengte 1 behouden. We komen dan op de volgende formule:
$$x_{herschaald\_ ti} = i - 1 + \ \frac{x_{ti} - \min(x_{ti})}{\max(x_{ti}) - \min(x_{ti})}$$
Hierbij staat i voor de waarde behorende tot de toetsadviescategorie: pro/vmbo b (1), vmbo b/k (2), vmbo k/gt (3), vmbo gt/havo (4), havo/vwo (5) en vwo (6) en t voor de toetsaanbieder.
Om ervoor te zorgen dat de scores over de toetsadviezen niet overlappen, bijvoorbeeld de maximum score in categorie 1 en de minimum score in categorie 2, doen we nog een kleine aanpassing zodat dit niet kan gebeuren. We passen de min(x) en max(x) per cel van de toetsaanbieder en het toetsadvies aan door van het minimum 0,5 af te trekken en bij het maximum 0,5 op te tellen. Door dit te doen krijg je minimum- en maximumscores die precies tussen de ranges van de twee toetsadviezen in liggen, bijvoorbeeld bij CET zal de maximumscore voor pro/vmbo b en de minimumscore voor vmbo b/k op 510,5 liggen wat precies tussen de waarden 510 en 511 is, die de grens vormen tussen beide toetsadviezen. De schaal zal op die manier ook netjes verdeeld zijn tussen de toetsadviezen. De aangepaste formule is als volgt:
$$x_{herschaald\_ ti} = i - 1 + \ \frac{x_{ti} - (\min\left( x_{ti} \right) - 0,5)}{(max\left( x_{ti} \right) + 0,5) - (\min\left( x_{ti} \right) - 0,5)}$$
Een normalisatie met min-max transformatie past beter bij een situatie waarin de onderliggende toetsaanbieders verschillende verdelingen hebben. Het voordeel is dat alles op dezelfde schaal komt te liggen én we rekening kunnen houden met de toetsadviezen.
Methode 3: Normalisatie met min-max transformatie naar toetsaanbieder en toetsadvies + correctie van de schaalverdeling over de toetsadviezen
In tabel 5.2.1 zien we dat het bereik van de eindtoetsscores over de toetsadviezen nog kan verschillen. Bijvoorbeeld, het bereik voor pro/vmbo b voor Iep is smaller dan het bereik voor vmbo k/gt. Met methode 2 hebben we alle toetsadviezen een bereik van dezelfde lengte gegeven op de schaal, namelijk (i-1,i) bij toetsadvies i. In methode 3 stellen we voor om ook dit bereik nog te herschalen zodat we rekening houden met hoe vaak de toetsadviezen voorkomen in de populatie. Op deze manier brengen we de schaal meer in verhouding met de realiteit. De bereiken per toetsadvies die bij methode 2 gelijk waren aan 1 zullen dus aangepast kunnen worden naar een passend bereik op basis van verhoudingen in de populatie.
De frequenties waarin de toetsadviezen voorkomen – over alle toetsaanbieders heen – worden in figuur 5.2.7 weergegeven. Daarbij zien we dat de middelste toetsadviezen vaker voorkomen dan de toetsadviezen die daarna of daarvoor volgen.
| Toetsadvies | Aantal (Aantal ) |
|---|---|
| Pro/vmbo b | 4593 |
| Vmbo b/k | 24317 |
| Vmbo k/gt | 35559 |
| Vmbo gt/havo | 50999 |
| Havo/vwo | 32988 |
| Vwo | 29226 |
We nemen in dit geval aan dat onderliggende toetsadviezen ongeveer normaal verdeeld zijn in de populatie. Daarom passen we de schaalgrenzen zo aan dat ze aansluiten bij die van een normale verdeling. Dat doen we in de volgende stappen:
- We berekenen het aandeel leerlingen per toetsadvies voor de totale populatie en berekenen hierbij het cumulatieve aandeel.
- Vervolgens gaan we uit van een normale verdeling met een gemiddelde van 3 en een standaarddeviatie van 1. Op deze manier sluiten we aan bij de schaal uit methode 2 die loopt van [0, 6], met 3 als middelpunt. De schaal past het beste bij deze toepassing, maar je zou ook een andere schaalverdeling kunnen hanteren. Vervolgens zoeken we op basis van de cumulatieve proporties per toetsadvies de juiste grenzen op in de normale verdeling. Hieronder staat een voorbeeld voor pro/vmbo-b. Dit toetsadvies heeft een cumulatieve proportie van 0,0258 en daarbij hoort de grens in de normale verdeling van 1,0544.
- Omdat de staarten van de normale verdeling oneindig zijn en geen harde grens hebben, zetten wij deze op 0 en 6. (Dit afkappen heeft slechts een zeer beperkt effect op de uitkomsten, aangezien een trekking uit de normale verdeling N(3,1) met ruim 99,7% kans ligt tussen 0 en 6). Zo loopt de schaal voor pro vmbo-b van 0 tot 1,0544. Deze methode kunnen we toepassen op elk toetsadvies. Hierbij nemen we ook weer de aangepaste min(x) en max(x) waarden mee zoals beschreven bij methode 2, om precies tussen de toetsadviezen uit te komen.
- Vervolgens normaliseren we de eindtoetsscores weer opnieuw, maar dan met de schaalgrenzen per toetsadvies i, aangepast naar de normale verdeling:
$$x_{herschaald\_ ti} = a_{i} + \ \frac{(x_{ti} - \left( \min\left( x_{ti} \right) - 0,5 \right))*(b_{i} - a_{i})}{(max\left( x_{ti} \right) + 0,5) - (\min\left( x_{ti} \right) - 0,5)}$$
Hierbij staat ai voor de ondergrens voor toetsadviescategorie i en bi voor de bovengrens. Beide grenzen zijn gebaseerd op de normale verdeling behorende bij het cumulatieve aandeel van de betreffende toetsadviescategorie.
5.3 Resultaten
In figuur 5.3.1 wordt het resultaat van de uniformering van de eindtoetsscores weergegeven voor de verschillende methoden. In de eerste figuur (linksboven) zien we de oorspronkelijke verdeling. In de tweede figuur (rechtsboven) zien we methode 1 met z-scores, figuur 3 (linksonder) de methode met min-max transformatie en in figuur vier (rechtsonder) de methode met de min-max transformatie én extra herschaling naar een normale verdeling.
Methode 2 (min-max normalisatie) zet alles netjes op een schaal van 0 tot 6, maar heeft nog vrij uitgesmeerde verdelingen tussen 0 en 6. Bij methode 3 (min-max normalisatie + herschaling) zien we dat de verdeling in totaal wel meer lijkt op een normale verdeling. Terwijl bij methode 1 (z-scores) alles nog dichter bij elkaar komt te liggen in het middelpunt. Wel valt op dat AMN en Dia een vrij vlakke verdeling blijven houden in alle scenario’s, zoals we ook terugzien in de oorspronkelijke scores. De grootste toetsaanbieders domineren de uitkomst het meest bij het gebruik van z-scores. Daarnaast houden de z-scores geen rekening met bijbehorende toetsadviezen, terwijl de andere normalisaties dit wel doen. Door het gebruik van min-max normalisatie krijgen we een praktische schaal van 0 tot 6. Door dit ook nog te herschalen komen we in de buurt van een normale verdeling, maar houden we ook nog vast aan de oorspronkelijke verdelingen per toetsaanbieder. We sluiten hierbij meer aan bij de verhoudingen in de populatie én houden vast aan de toetsadviezen die hierbij horen.
Het nadeel van z-scores is dat we geen rekening houden met de toetsadviezen. Dit kan betekenen dat scores gaan overlappen over toetsadviezen heen. In tabel 5.3.2 wordt duidelijk dat dit inderdaad gebeurt. Bijvoorbeeld: een z-score van –1 hoort een toetsadvies vmbo- k/gt als deze afkomstig is van CET, maar een toetsadvies vmbo-b/k als deze afkomstig is van Route 8.
We hebben de nieuwe voorkomende bereiken toegevoegd aan tabel 5.2.1 om een voorbeeld te geven van de nieuwe herschaalde scores, zie tabel 5.3.2.
| Toetsadvies | CET | Route 8 | Iep | Dia | AMN | Z-scores | min-max normalisatie | min-max normalisatie + herschaling |
|---|---|---|---|---|---|---|---|---|
| Pro / vmbo b | 501-510 | 100-112 | 50-51 | 321-338 | 300-304 | -3,49 – (-1,34) | 0,03-0,97 | 0,03-1,03 |
| Vmbo b/k | 511-523 | 113-159 | 52-68 | 339-349 | 305-332 | -2,47 – (-0,67) | 1,01-1,99 | 1,06-2,01 |
| Vmbo k/gt | 524-531 | 160-187 | 69-76 | 350-356 | 333-374 | -1,13 – (-0,06) | 2,01-2,99 | 2,02-2,64 |
| Vmbo gt/havo | 532-539 | 188-216 | 77-84 | 357-365 | 375-433 | -0,31 – 0,75 | 3,02-3,99 | 2,66-3,38 |
| Havo/vwo | 540-544 | 217-238 | 85-91 | 366-371 | 434-468 | 0,43 – 1,31 | 4,01-4,99 | 3,39-3,97 |
| Vwo | 545-550 | 239-300 | 92-100 | 372-390 | 469-500 | 1,03 – 2,57 | 5,01-5,99 | 3,99-5,98 |
5.4 Conclusie en discussie
Om de eindtoetsen zo goed mogelijk te uniformeren met de beschikbare gegevens, zou methode 3 met min-max normalisatie én herschaling de voorkeur hebben. Met deze methode zetten we alles op eenzelfde schaal en houden we rekening met het aandeel per toetsadvies in de populatie en bijbehorende toetsadviezen.
Daarnaast hebben we bij methode 3 gekozen voor een normale verdeling om te herschalen. Hier zou ook een andere methode bedacht kunnen worden om te herschalen. Tevens is de keuze voor een normale verdeling met een gemiddelde van 3 en standaarddeviatie van 1 een pragmatische. Dit zou ook iets anders kunnen zijn als basis. Omdat de ranges over de toetsadviezen, in combinatie met de toetsaanbieders kunnen verschillen, kunnen we niet zomaar wegen naar deze ranges.
Hoewel methode 3 de beste benadering is voor uniformering met de huidige data, zijn er nog steeds enkele kanttekeningen te maken. Bij de voorgestelde methoden wordt de aanname gemaakt dat alle toetsen ook werkelijk hetzelfde meten bij leerlingen. We kunnen op dit moment niet beoordelen of dit daadwerkelijk het geval is. We zien daarnaast in de figuren terug dat de verdeling van de eindtoetsscores verschilt per toetsaanbieder. De toetsen bestaan wel uit enkele ankeritems op rekenen en taal die terugkomen in alle toetsen, maar de overige inhoud van de toetsen zou wel kunnen verschillen. Dit kunnen we op dit moment niet beoordelen. Daarnaast zou de populatie per eindtoets kunnen verschillen, doordat scholen verschillend een keuze maken voor een bepaalde eindtoets. Zo stelde het CPB eerder in een rapport vast dat scholen met een slechtere uitkomst op de eindtoets eerder geneigd zijn om te kiezen voor een andere toets dan de Centrale Eindtoets (CET) van Cito (Swart, L., Van den Berge, W., & Visser, D., 2019).
Om rekening te houden met bovenstaande kanttekeningen zou er verder onderzocht moeten worden of er systematische verschillen voorkomen tussen scholen én leerlingen. We zouden ten eerste kunnen corrigeren voor het type eindtoets, door dit mee te nemen als predictor in het uiteindelijke onderwijsachterstandenmodel. Wanneer hierbij duidelijk wordt dat deze predictor verschillen verklaart in de onderwijsprestatie, zal dit een indicatie kunnen zijn dat er systematische verschillen zijn tussen de verschillende eindtoetsen. Daarnaast kan een dergelijke uitkomst ook gebruikt worden om de uniformeringsmethode te verbeteren. Ook zouden we het model kunnen toepassen per toetspopulatie om te zien of er verschillen naar voren komen. Daarnaast zou er gekeken moeten worden wat de kenmerken zijn van scholen per type eindtoets en welke scholen zijn overgestapt van CET naar een andere type eindtoets. We zouden dit bijvoorbeeld kunnen koppelen aan de historische onderwijsprestatie op CET van de scholen. Wanneer het type eindtoets systematisch verschilt per type school, kunnen we wel hiervoor corrigeren door achtergrondkenmerken mee te nemen die deze verschillen verklaren. Om dus werkelijk verder te gaan met methode 3, moet er verder in kaart worden gebracht of de assumptie dat de eindtoetsen hetzelfde meten bij leerlingen kan worden gehouden.
6. Expert raadpleging
6.1 Inleiding
Als voorbereiding op de ontwikkeling van een nieuw model voor het risico op onderwijsachterstand is het noodzakelijk om zicht te hebben op welke achtergrondkenmerken van kinderen in potentie bij kunnen dragen aan het schatten van het risico op onderwijsachterstand. Middels het bevragen van experts op het gebied van onderwijsachterstanden kan een overzicht worden opgesteld van achtergrondkenmerken die mogelijk een bijdrage kunnen leveren aan een nieuw model. Dit overzicht zal worden aangevuld met de uitkomsten van literatuuronderzoek (CBS, 2024).6.2 Methode
Door middel van een Delphi-studie kan op systematische wijze de kennis van meerdere experts verzameld worden. Anonimiteit staat hierin centraal: er is geen interactie tussen de experts. Dit zorgt ervoor dat de experts niet beïnvloed worden door elkaars antwoorden. Na iedere ronde worden de uitkomsten door CBS-onderzoekers samengevat en weer in een volgende ronde voorgelegd aan de experts. In de huidige studie is gekozen voor twee rondes waarin experts per e-mail gevraagd zijn om antwoord te geven op onze vragen. De experts in ons onderzoek zijn allen wetenschappers die (onder andere) onderzoek doen op het gebied van onderwijsachterstanden.
Ronde 1
Het doel van ronde 1 was om factoren in kaart te brengen die bijdragen aan het risico op onderwijsachterstand in het Nederlandse basisonderwijs. Aan de experts zijn de volgende vragen voorgelegd:
- Welke factoren dragen volgens u bij aan risico op onderwijsachterstand in het Nederlandse basisonderwijs?
- Welke academische literatuur beschrijft de door u genoemde factoren? U hoeft hiervoor geen literatuurzoekopdracht uit te voeren. Het gaat hierbij om verwijzingen die u gemakkelijk (uit het hoofd) kunt reproduceren.
- In het geval van buitenlands onderzoek, kunt u kort reflecteren op mogelijke relevantie voor de Nederlandse (onderwijs)context?
Ronde 2
Voor ronde 2 hebben wij de antwoorden uit ronde 1 samengevat en gecategoriseerd in vier gebieden: de gezinssituatie, het kind, de school, en de omgeving. Aan de experts werd vervolgens gevraagd om 10 factoren uit de lijst te selecteren die volgens hen de belangrijkste risicofactoren van onderwijsachterstand zijn.
6.3 Resultaten
In de eerste ronde hebben wij aan de 10 deelnemende experts onze vragen voorgelegd. Zes van hen hebben een inhoudelijke reactie gegeven. In ronde 2 ontvingen wij van vijf van deze zes experts een inhoudelijke bijdrage.
Ronde 1
In ronde 1 werd aan de experts gevraagd wat volgens hen factoren zijn die bijdragen aan het risico op onderwijsachterstand in het Nederlandse basisonderwijs. Er werden door de experts ook risicofactoren genoemd die niet beschikbaar zijn in onze registerdata. Voor deze factoren is allereerst een proxy geprobeerd te vinden en wanneer dit niet lukte, werd de factor buiten beschouwing gelaten in ronde 2. De volledige lijst van de in ronde 1 genoemde risicofactoren is te vinden in Bijlage 4.
Ronde 2
Voor ronde 2 hebben wij de factoren die beschikbaar zijn (al dan niet via een proxy) onderverdeeld in de volgende gebieden: gezinssituatie, kind, school, en omgeving. Experts gaven vervolgens aan welke tien risicofactoren voor onderwijsachterstand volgens hen het belangrijkst waren. In Bijlage 5 is per risicofactor te zien hoeveel experts de betreffende factor in hun top 10 hebben gezet. De factoren die in ronde 2 door minstens twee experts zijn aangemerkt als belangrijkste factoren worden hieronder nader beschreven.
Gezinssituatie:
- Opleidingsniveau van de ouders
Eerdere studies laten zien dat er een verband is tussen het opleidingsniveau van de ouders en onderwijsachterstanden van het kind. Dit verband kan door verschillende mechanismen worden verklaard. Zo worden kinderen van lager opgeleide ouders cognitief vaak minder gestimuleerd: ze hebben beperkte toegang tot educatieve hulpbronnen zoals boeken, computers en buitenschoolse activiteiten (Mesman, 2020; Haelermans et al, 2022). Ook laten studies zien dat leraren geneigd zijn de prestaties en mogelijkheden van kinderen van lager opgeleide ouders te onderschatten, wat de leerprestaties negatief kan beïnvloeden (Weinberg et al., 2019; Timmermans, Kuyper & van der Werf, 2015; Mulder et al., 2014) . Daarnaast laten lager opgeleide ouders vaak minder betrokkenheid bij het onderwijs zien dan hoger opgeleide ouders. Ook dit kan de leerresultaten negatief beïnvloeden (Mulder et al., 2014). - Werkstatus van de ouders
Vooral werkloosheid van de vader lijkt samen te hangen met slechtere leerprestaties van het kind (Mooi-Reci et al., 2019). Werkende ouders spenderen wellicht minder tijd met hun kind dan niet-werkende ouders, maar niet zozeer minder kwalitatieve tijd. En juist dat laatste is belangrijk voor de cognitieve ontwikkeling van een kind ( Schildberg-Hörisch, 2016). - Eenoudergezin
Leerlingen uit eenoudergezinnen presteren vaak lager op school dan leerlingen die bij beide ouders wonen. Dit kan verklaard worden door de afwezigheid van hulpbronnen en financiële stress, maar ook door emotionele problemen en stress als gevolg van een scheiding (Lange & Dronkers, 2018). - Langdurige betalingsachterstanden (proxy voor chronische financiële stress/armoede)
Behalve het gebrek aan hulpbronnen dat kan ontstaan in geval van schulden of armoede, kan dagelijkse stress die dit met zich mee brengt ook invloed hebben op de opvoeding. Zo stelt Mesman (2020) dat deze stress kan leiden tot minder sensitief opvoeden wat weer een negatieve invloed heeft op de cognitieve ontwikkeling van het kind. - Gezinsinkomen
Leerlingen uit gezinnen met een lager inkomen presteren gemiddeld slechter op school dan hun leeftijdgenoten uit gezinnen met een hoger inkomen (Zumbuehl & Dillingh, 2020). Ook hieraan kan bijvoorbeeld een gebrek aan hulpbronnen, maar ook financiële stress ten grondslag liggen. - Ingrijpende levensgebeurtenissen
Hieronder worden levensgebeurtenissen verstaan als verhuizing, overlijden van een gezinslid of ernstige ziekte van het kind of gezinslid. - Niet-westerse migratieachtergrond (ouders en grootouders)
Onderpresteren komt vaker voor bij leerlingen met een niet-westerse migratieachtergrond dan bij leerlingen zonder migratieachtergrond (Driessen, 2012; Entorf, 2015; Zumbuehl & Dillingh, 2020). Ook hier lijken de verwachtingen van leraren weer een rol te spelen, evenals het opleidingsniveau van de ouders, ouderbetrokkenheid, beschikbaarheid van hulpbronnen en taalbeheersing van de ouders en het kind zelf (Entorf, 2015; Fleischmann & de Haas, 2016; Sylke, 2024). - Verblijfsduur van de ouders in Nederland
Bij de huidige indicator wordt alleen de verblijfsduur van één ouder - de moeder - gebruikt omdat er een hoge correlatie is tussen de verblijfsduur van beide ouders. - Beperkte Nederlandse taalvaardigheid bij moeder en daardoor bij kind
School:
- Proportie leerlingen met een lage SES op school/in de klas
Leerlingen op scholen met een hoge gemiddelde SES presteren vaak beter dan leerlingen op scholen met een lage gemiddelde SES (Belfi, Haelermans & Fraine, 2016). Dit komt mogelijk doordat leraren op deze scholen lagere verwachtingen hebben. Ook kunnen leerlingen mogelijk eerder een negatieve leerhouding en negatief leergedrag van leeftijdsgenoten overnemen. - Percentage achterstandsleerlingen op school
Voor de proportie achterstandsleerlingen op een school is eenzelfde samenhang met leerprestaties te verwachten als voor de proportie leerlingen met een lage SES op een school (Bluemink et al, 2022; Mulder et al., 2014).
Omgeving:
- Gemiddelde SES van de buurt
Een lage gemiddelde SES van een buurt kan leerprestaties negatief beïnvloeden( Kuyvenhoven & Boterman, 2020; Nieuwenhuis & Hooimeijer, 2016). - Aandeel huishoudens onder de armoedegrens in de buurt
Er is een samenhang tussen armoede in de buurt en lagere leerprestaties( Nieuwenhuis & Hooimeijer, 2016).
Voor zowel SES als armoede op buurtniveau geldt dat er verschillende mechanismen een rol kunnen spelen(Kuyvenhoven & Boterman, 2020). Zo kan het aanbod van hulpbronnen in de buurt (bijvoorbeeld bibliotheken en wijkcentra) effect hebben op de cognitieve ontwikkeling en leerprestaties. Daarnaast is er een mechanisme genaamd ‘collectieve socialisatie’ wat wil zeggen dat mensen individueel beïnvloed worden door de sociale organisatie van hun buurt (bijvoorbeeld de sociale controle, normen en waarden en rolmodellen). Ook kunnen de houding en het gedrag van leeftijdsgenoten uit de buurt het leergedrag van kinderen direct beïnvloeden. Het is ook mogelijk dat een deel van het effect verklaard kan worden door de kenmerken van de scholen in deze buurten (zie School).
6.4 Samenvatting en conclusies
De expertraadpleging heeft een bruikbare set aan achtergrondkenmerken opgeleverd. Deze set aan kenmerken vertoont grote overeenkomsten met de kenmerken zoals die bij de oorspronkelijke ontwikkeling van de risico-indicator onderwijsachterstanden zijn onderzocht (CBS, 2016). Ook zijn er sterke overeenkomsten met de uitkomsten van de literatuurstudie die is uitgevoerd (CBS, 2024).
Bijlage 1. Referenties
Belfi, B., Haelermans, C., & De Fraine, B. (2016). The long‐term differential achievement effects of school socioeconomic composition in primary education: A propensity score matching approach. British Journal of Educational Psychology, 86(4), 501-525.
Bethlehem, J. (2007). Methodenreeks: wegen als correctie voor non-respons. Rapport, CBS, Den Haag.
Bluemink, C., Jenniskens, T., Langen, A. V., Leest, B., & Wolbers, M. (2022). Onderpresteren in het Nederlandse basisonderwijs anno 2021. KBA Nijmegen.
Buuren, S. van, Groothuis-Oudshoorn, K. (2011). mice: Multivariate Imputation by Chained Equations in R. Journal of Statistical Software, 45(3), 1-67. DOI 10.18637/jss.v045.i03
CBS. (2016). Herziening gewichtenregeling primair onderwijs – Fase I. Rapport, CBS, Den Haag.
CBS. (2019). De nieuwe onderwijsachterstandenindicator primair onderwijs – Samenvattend rapport. Rapport, CBS, Den Haag.
CBS. (2024). Hoe kan de Landelijke Jeugdmonitor bijdragen aan het monitoren van kansenongelijkheid?
Daalmans, J. (2021). Notitie stuurgroep imputatie opleidingsniveau 2021-07-11. Intern document, CBS, Den Haag.
Driessen, G. (2012). Trends in Educational Disadvantage in Dutch Elementary School.
Entorf, H. (2015). Migrants and educational achievement gaps. IZA World of Labor.
Fleischmann, F., & de Haas, A. (2016). Explaining parents' school involvement: The role of ethnicity and gender in the Netherlands. The Journal of Educational Research, 109(5), 554-565.
Haelermans, C., Korthals, R., Jacobs, M., de Leeuw, S., Vermeulen, S., van Vugt, L., ... & de Wolf, I. (2022). Sharp increase in inequality in education in times of the COVID-19-pandemic. Plos one, 17(2), e0261114.
Johnson, N.L., S. Kotz & N. Balakrishnan (1994), Continuous univariate distributions, Volume 1. John Wiley & Sons, New York.
Kish, L. (1992). Weighting for Unequal Pi. Journal of Official Statistics 8, pp. 183–200.
Kuyvenhoven, J., & Boterman, W. R. (2021). Neighbourhood and school effects on educational inequalities in the transition from primary to secondary education in Amsterdam. Urban Studies, 58(13), 2660-2682.
Linder, F., van Roon, D. en Bakker, B. (2011). Combining Data from Administrative Sources and Sample Surveys; the Single-Variable Case. Case Study: Educational Attainment. In: Final Report, Work Package 4.2, ESSnet Project ‘Data Integration’.
Lange, M. de, & Dronkers, J. (2018). Single parenthood and children’s educational performance: inequality among families and schools. In The triple bind of single-parent families (pp. 125-144). Policy Press.
Mesman, J. (2010). Oud geleerd, jong gedaan: Investeren in ouders bevordert onderwijskansen van kinderen. Universiteit Leiden.
Mooi-Reci, I., Bakker, B., Curry, M., & Wooden, M. (2019). Why parental unemployment matters for children’s educational attainment: empirical evidence from The Netherlands. European Sociological Review, 35(3), 394-408.
Mulder, C. W. J., Fettelaar, D., Schouwenaars, I., Ledoux, G., Dikkers, L., & Kuiper, E. (2014). De achterstand van autochtone doelgroepleerlingen Oorzaken en aanpak. ITS Radboud Universiteit Nijmegen, Nijmegen
Nieuwenhuis, J., & Hooimeijer, P. (2016). The association between neighbourhoods and educational achievement, a systematic review and meta-analysis. Journal of Housing and the Built Environment, 31, 321-347.
R Core Team. (2023). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria.
Scholtus, S. en Pannekoek, J. (2015). Massa-imputatie van opleidingsniveaus. Rapport (PPM-2015-12-11-SSHS-JPNK). CBS, Den Haag.
Schildberg-Hörisch, H. (2016). Parental employment and children’s academic achievement. IZA World of Labor.
Schnepf, S. V. (2004). How different are immigrants? A cross-country and cross-survey analysis of educational achievement. A Cross-Country and Cross-Survey Analysis of Educational Achievement (November 2004).
Swart, L., Van den Berge, W., & Visser, D. (2019). De waarde van eindtoetsen in het primair onderwijs. CPB notitie.
Timmermans, A. C., Kuyper, H., & van der Werf, G. (2015). Accurate, inaccurate, or biased teacher expectations: Do Dutch teachers differ in their expectations at the end of primary education?. British Journal of Educational Psychology, 85(4), 459-478.
Venables, W. N. & Ripley, B. D. (2002). Modern Applied Statistics with S. Fourth Edition. Springer, New York. ISBN 0-387-95457-0
Weinberg, D., Stevens, G. W., Finkenauer, C., Brunekreef, B., Smit, H. A., & Wijga, A. H. (2019). The pathways from parental and neighbourhood socioeconomic status to adolescent educational attainment: An examination of the role of cognitive ability, teacher assessment, and educational expectations. Plos one, 14(5), e0216803.
Zumbuehl, M., & Dillingh, R. (2020). Ongelijkheid van het jonge kind. Den Haag: Centraal Planbureau.
Bijlage 2. Afleiding parameter K
De onderstaande afleiding is gebaseerd op een soortgelijke afleiding uit het rapport “Herziening gewichtenregeling primair onderwijs – Fase 3: bijschatting voor niet-ingeschreven leerlingen”.
Noteer de onderwijsscore van leerling i als yi. Een algemene formule voor de achterstandsscore zonder drempel van school j met een populatie van bekostigde leerlingen Uj is gegeven door:
$$S_{j}(q) = \sum_{i \in U_{j}}^{}{I\left\{ y_{i} \leq y_{L}(q) \right\}\left( y_{ref} - y_{i} \right)}. \tag{1}$$
Hierbij is yref een referentiescore en yL (q) de score die hoort bij het q × 100%-percentiel van de verdeling van onderwijsscores. Verder is I{.} een indicatorfunctie die gelijk is aan 1 als het argument waar is en anders gelijk aan 0. De achterstandsscore (zonder drempel) waarmee in de praktijk wordt gewerkt is een speciaal geval van (1) met q = 0,15 en \(y_{ref} = \overline{y}\) (het landelijke gemiddelde).
In het vervolg nemen we ter vereenvoudiging aan dat de populatie leerlingen bestaat uit M strata, waarbij de bijdrage van een leerling aan de variantie van de achterstandsscore constant is per stratum. We stellen voor om in de praktijk de volgende M = 7 strata te onderscheiden:
| Stratum | Omschrijving |
|---|---|
| 1 | opleidingsniveau van beide ouders onbekend, onderwijsscore direct bepaald |
| 2 | opleidingsniveau van beide ouders onbekend, onderwijsscore geïmputeerd |
| 3 | opleidingsniveau alleen van moeder bekend, onderwijsscore direct bepaald |
| 4 | opleidingsniveau alleen van moeder bekend, onderwijsscore geïmputeerd |
| 5 | opleidingsniveau alleen van vader bekend, onderwijsscore direct bepaald |
| 6 | opleidingsniveau alleen van vader bekend, onderwijsscore geïmputeerd |
| 7 | opleidingsniveau van beide ouders bekend, onderwijsscore direct bepaald óf leerling komt voor in een bestand van COA of IND |
De reden om voor deze indeling in strata te kiezen is dat de hoeveelheid beschikbare informatie per stratum verschilt, wat mogelijk leidt tot verschillende bijdragen per stratum aan de variantie van de achterstandsscore op schoolniveau. Voor leerlingen die voorkomen in de registraties van het COA en de IND wordt een vaste score geïmputeerd: hun variantiebijdrage is daarom praktisch nul. Dit laatste hebben zij gemeenschappelijk met alle kinderen voor wie van beide ouders het opleidingsniveau bekend is; vandaar dat deze twee deelpopulaties zijn samengenomen tot één stratum. De overige strata komen overeen met een indeling die is gebruikt in de Jaarlijkse monitor Risico-indicator onderwijsachterstanden Primair Onderwijs.
We noteren de fractie leerlingen
op school j die behoren tot stratum g als pjg, met 0 ≤ pjg ≤ 1 (g = 1,…,7). Per definitie geldt: pj1 + pj2 + pj3 + pj4 + pj5 + pj6 + pj7 = 1 voor elke school.
Stel dat de achterstandsscore zonder drempel Sj = Sj (q) voor school j met nj bekostigde leerlingen (of algemener: een groep van nj kinderen) twee keer onafhankelijk zou worden berekend op basis van dezelfde brongegevens, met als resultaat de scores Sj1 en Sj2. Omdat de twee scores onafhankelijk van elkaar zijn7), geldt voor de variantie van het verschil Sj2 -Sj1:
$${var}\left( S_{j2} - S_{j1} \right) = {var}\left( S_{j1} \right) + {var}\left( S_{j2} \right) = 2{var}\left( S_{j} \right).$$
Dat wil zeggen:
$${var}\left( S_{j} \right) = \frac{{var}\left( S_{j2} - S_{j1} \right)}{2}. \tag{2}$$
Een formule voor var(Sj) kan daarom worden afgeleid uit een formule voor var(Sj2 - Sj1).
Bij de twee onafhankelijke berekeningen horen strikt genomen ook aparte waarden voor de grootheden yref, yL (q) en (bij scores met drempel) yref,L (q). Zeg: yref,1, yL,1 (q) bij de eerste berekening en yref,2, yL,2 (q) bij de tweede berekening. De variatie in deze grootheden is echter veel kleiner dan die in de achterstandsscores per school, omdat ze worden geschat uit de volledige populatie (meer dan een miljoen leerlingen). We kunnen de stochastiek in deze grootheden daarom verwaarlozen en we zullen ze hieronder behandelen als constanten.
De twee achterstandsscores Sj1 en Sj2 zijn gebaseerd op onafhankelijk van elkaar berekende individuele onderwijsscores. Noteer deze onderwijsscores voor leerling i als yi1 en yi2. Volgens formule (1) is Sj2 - Sj1 voor een school met leerlingenpopulatie Uj te schrijven als:
$$S_{j2} - S_{j1} = \sum_{i \in U_{j}}^{}\left\lbrack I\left\{ y_{i2} \leq y_{L,2}(q) \right\}\left( y_{ref,2} - y_{i2} \right) - I\left\{ y_{i1} \leq y_{L,1}(q) \right\}\left( y_{ref,1} - y_{i1} \right) \right\rbrack \equiv \sum_{i \in U_{j}}^{}z_{i}$$
Beschouw eerst de situatie dat een school uitsluitend leerlingen heeft die zijn ingeschreven in één bepaald stratum. Op basis van hun onderwijsscores yi1 en yi2 kunnen deze leerlingen worden verdeeld in vier groepen, elk met een eigen bijdrage zi aan het verschil Sj2 - Sj1:
yi2 ≥ yL,2 (q) yi2 < yL,2 (q)
yi1 ≥ yL,1 (q) groep W groep X
bijdrage: zi = 0 bijdrage: zi = yref,2 - yi2
yi1 < yL,1 (q) groep Y groep Z
bijdrage: zi = yi1 - yref,1 bijdrage: zi = yi1 - yi2
Voor leerlingen in groep W vallen beide realisaties van de onderwijsscore boven de ondergrens yL (q). De bijdragen van deze leerlingen aan Sj1 en Sj2 zijn beide gelijk aan nul. Voor leerlingen in groep X en Y valt een van beide onderwijsscores onder yL (q) en de andere erboven. De bijdrage aan Sj2 - Sj1 is daarom zi=yref,2 - yi2 (groep X) of zi=yi1 - yref,1 (groep Y). In de onderstaande afleiding is voor deze leerlingen relevant wat de gemiddelde waarde van deze bijdrage is en wat de variantie daaromheen is. Definieer:
$$\begin{align} \mu_{XY} &= E\left( y_{ref,2} - y_{i2} \middle| i \in X \right) = - E\left( y_{i1} - y_{ref,1} \middle| i \in Y \right)\\ \omega_{XY}^{2} &= {var}\left( y_{ref,2} - y_{i2} \middle| i \in X \right) = {var}\left( y_{i1} - y_{ref,1} \middle| i \in Y \right). \end{align}$$
Ter vereenvoudiging is hierbij aangenomen dat (per stratum) alle leerlingen in groep X (en Y) dezelfde verwachting en dezelfde variantie hebben. De gelijkheden E(yref,2 - yi2│i ∈ X) = - E(yi1 - yref,1)│i ∈ Y) en var(yref,2 - yi2│i ∈ X)=var(yi1 - yref,1│i ∈ Y) volgen uit symmetrie-overwegingen, aangezien beide scores yi1 en yi2 afkomstig zijn uit dezelfde verdeling.
Voor leerlingen in groep Z vallen beide onderwijsscores onder yL (q). De bijdrage aan het verschil Sj2 - Sj1 is zi = yi1 - yi2. In verwachting is dit verschil gelijk aan nul. Voor de variantie van het verschil wordt de volgende parameter ingevoerd:
$$\sigma_{Z}^{2} = {var}\left( y_{i1} - y_{i2} \middle| i \in Z \right)$$
Ook hier is de vereenvoudigende aanname gemaakt dat deze variantie (per stratum) voor alle leerlingen in groep Z gelijk is. Definieer ten slotte de kans dat een willekeurig gekozen leerling in groep V valt als πV (met V ∈ {W,X,Y,Z}).
De onderwijsscores zijn bij benadering onafhankelijk tussen verschillende leerlingen. (De gebruikte imputatiemethoden introduceren enige afhankelijkheid tussen de scores, maar deze kan worden verwaarloosd.) Onder de aanname dat de onderwijsscores onafhankelijk zijn tussen leerlingen volgt:
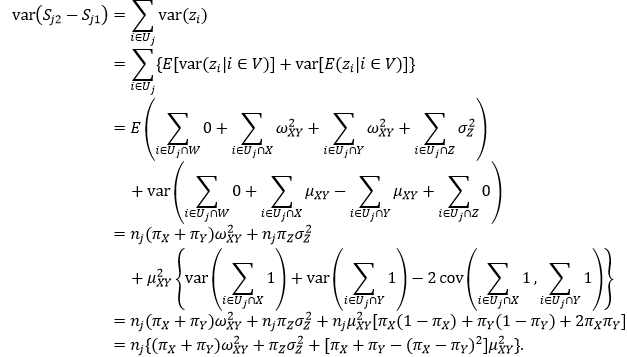
In de tweede regel is een standaard-variantiedecompositie gebruikt, waarbij in de binnenste variantie en verwachting is geconditioneerd op de groep (W, X, Y of Z) waarin leerling i valt. In de een-na-laatste regel is gebruikgemaakt van eigenschappen van een multinomiale verdeling.
Stel nu dat de school leerlingen kan bevatten uit alle strata van de populatie die hierboven zijn gedefinieerd, waarbij pjg de fractie leerlingen uit stratum g aanduidt. Per stratum hebben de geïmputeerde scores mogelijk andere eigenschappen. Daarom moeten aparte parameters worden ingevoerd per stratum. De kans dat een willekeurig gekozen leerling uit stratum g in groep V valt wordt genoteerd als πVg (V ∈ {W,X,Y,Z}). Definieer verder:
$$\begin{align}
\mu_{XYg} &= E\left( y_{ref,2} - y_{i2} \middle| i \in X,g \right) = - E\left( y_{i1} - y_{ref,1} \middle| i \in Y,g \right),\\
\omega_{XYg}^{2} &= {var}\left( y_{ref,2} - y_{i2} \middle| i \in X,g \right) = {var}\left( y_{i1} - y_{ref,1} \middle| i \in Y,g \right),\\
\sigma_{Zg}^{2} &= {var}\left( y_{i1} - y_{i2} \middle| i \in Z,g \right).
\end{align}$$
Analoog aan het voorafgaande kan voor de variantie van Sj2 - Sj1 bij een school met pjg nj leerlingen uit stratum g worden afgeleid dat:
$${var}\left( S_{j2} - S_{j1} \right) = n_{j}\sum_{g = 1}^{M}{p_{jg}\left\{ \left( \pi_{Xg} + \pi_{Yg} \right)\omega_{XYg}^{2} + \pi_{Zg}\sigma_{Zg}^{2} + \left\lbrack \pi_{Xg} + \pi_{Yg} - {(\pi_{Xg} - \pi_{Yg})}^{2} \right\rbrack\mu_{XYg}^{2} \right\}}.$$
Definieer:
$$K_{g} = \left( \pi_{Xg} + \pi_{Yg} \right)\omega_{XYg}^{2} + \pi_{Zg}\sigma_{Zg}^{2} + \left\lbrack \pi_{Xg} + \pi_{Yg} - {(\pi_{Xg} - \pi_{Yg})}^{2} \right\rbrack\mu_{XYg}^{2} \tag{3}$$
Uit (2) volgt nu dat
$${var}\left( S_{j} \right) = \frac{n_{j}}{2}\sum_{g = 1}^{M}{p_{jg}K_{g}}.$$
De grootheden Kg en de onderliggende parameters uit formule (3) hebben we in dit onderzoek geschat door voor de populatie van 2021 het volledige bijschattingsproces drie keer onafhankelijk uit te voeren. Dit geeft drie mogelijke paarsgewijze vergelijkingen tussen onderwijsscores: (yi1,yi2 ), (yi1,yi3 ) en (yi2,yi3 ).
8) Gelijk is de bijdrage in deze groep zi = yi1 - yi2 + yref,2 - yref,1. Zoals opgemerkt is het verschil yref,2 - yref,1 in de praktijk verwaarloosbaar klein. Het wordt hier daarom gemakshalve weggelaten.
Bijlage 3. Variantieschatting gebruikt in de validatiestudie
In deze bijlage leiden we een variantiebenadering af die in de validatiestudie uit hoofdstuk 3 is gebruikt.
Definieer δci = 1 als persoon i opleidingsniveau c heeft en anders δci = 0. Er is een steekproef van omvang n beschikbaar waar δci is waargenomen. Hieruit wordt de proportie personen met opleidingsniveau c geschat door:
$${\widehat{P}}_{c} = \frac{\sum_{i = 1}^{n}{w_{i}\delta_{ci}}}{\sum_{i = 1}^{n}w_{i}}$$
waarbij wi het ophooggewicht is van persoon i in de steekproef. Ter vereenvoudiging nemen we aan dat er (bij benadering) sprake is van een enkelvoudig aselecte steekproef en dat de steekproeffractie uit de doelpopulatie verwaarloosbaar klein is.
Verder zijn J=10 geïmputeerde versies van de steekproef beschikbaar. Definieer δimp,cij=1 als in ronde j opleidingsniveau c is geïmputeerd voor persoon i en anders δimp,cij=0. Uit de geïmputeerde data kan de proportie personen met opleidingsniveau c worden geschat door:
$${\overline{\widehat{P}}}_{imp,cJ} = \frac{1}{J}\sum_{j = 1}^{J}{\widehat{P}}_{imp,cj},\ \ \ \ {\widehat{P}}_{imp,cj} = \frac{\sum_{i = 1}^{n}{w_{i}\delta_{imp,cij}}}{\sum_{i = 1}^{n}w_{i}}$$
We zijn geïnteresseerd in de variantie van het verschil \({\overline{\widehat{P}}}_{imp,cJ} - {\widehat{P}}_{c}\) Deze variantie kan worden geschreven als:
$$\begin{align} var\left( \overline{\widehat{P}}_{imp,cJ} - \widehat{P}_{c} \right) &= E\left\{ var\left( \overline{\widehat{P}}_{imp,cJ} - \widehat{P}_{c} \middle| steekproef \right) \right\} + var\left\{ E\left( \overline{\widehat{P}}_{imp,cJ} - \widehat{P}_{c} \middle| steekproef \right) \right\} \\ &= E\left\{ var\left( \overline{\widehat{P}}_{imp,cJ} \middle| steekproef \right) \right\} + var\left\{ \overline{\widehat{P}}_{imp,c\infty} - \widehat{P}_{c} \right\} \\ &= \frac{1}{J} E\left\{ var\left( \widehat{P}_{imp,cj} \middle| steekproef \right) \right\} + var\left\{ \overline{\widehat{P}}_{imp,c\infty} - \widehat{P}_{c} \right\} \\ &= V_{1c} + V_{2c}, \end{align}$$
waarbij \({\overline{\widehat{P}}}_{imp,c\infty}\) de theoretische schatter is die gevonden zou worden als J→∞.
De variantie \(V_{2c} = {var}\left\{ {\overline{\widehat{P}}}_{imp,c\infty} - {\widehat{P}}_{c} \right\}\) kan bij benadering worden geschat door:
$$\begin{align} \widehat{V}_{2c} &= \frac{1}{n(n - 1)}\sum_{i = 1}^{n}\left( z_{ci} - \overline{z}_{c} \right)^{2},\\ z_{ci} &= \frac{1}{J}\sum_{j = 1}^{J}\delta_{imp,cij} - \delta_{ci}, \end{align}$$
met \({\overline{z}}_{c} = n^{- 1}\sum_{i = 1}^{n}z_{ci}\). In deze formule is nog geen rekening gehouden met de ophooggewichten wi. In de praktijk leiden ongelijke ophooggewichten doorgaans tot een hogere variantie. Een redelijke benadering van dit effect wordt vaak gegeven door de zogenaamde Kish-factor (Kish, 1992). Toevoegen van deze factor geeft:
$${\widehat{V}}_{2c} = \frac{1}{n(n - 1)}\sum_{i = 1}^{n}\left( z_{ci} - {\overline{z}}_{c} \right)^{2}\left( 1 + {CV}_{w}^{2} \right),$$
waarbij CVw de variatiecoëfficiënt van de ophooggewichten is (de standaarddeviatie van de gewichten gedeeld door het gemiddelde gewicht).
De andere term V1c kan bij benadering worden geschat met behulp van de empirische variantie van \({\widehat{P}}_{imp,cj}\) over de imputatieronden heen:
$${\widehat{V}}_{1c} = \frac{1}{J(J - 1)}\sum_{j = 1}^{J}\left( {\widehat{P}}_{imp,cj} - {\overline{\widehat{P}}}_{imp,cJ} \right)^{2}.$$
Samengevat vinden we dus de volgende variantieschatter:
$$\widehat{var}\left( {\overline{\widehat{P}}}_{imp,cJ} - {\widehat{P}}_{c} \right) = \frac{1}{J(J - 1)}\sum_{j = 1}^{J}\left( {\widehat{P}}_{imp,cj} - {\overline{\widehat{P}}}_{imp,cJ} \right)^{2} + \frac{1}{n(n - 1)}\sum_{i = 1}^{n}\left( z_{i} - \overline{z} \right)^{2}\left( 1 + {CV}_{w}^{2} \right).$$
Bijlage 4. Resultaten expertraadpleging ronde 1: risicofactoren onderwijsachterstand
Ouders/gezin
- Laag opleidingsniveau van ouders
- Beroep van ouders
- Eenoudergezinnen
- Veel kinderen in het gezin
- Jonge moeder
- Laag gezinsinkomen (netto)
- Laag eigen vermogen gezin
- (Problematische) schulden in gezin
- Chronische (financiële) stress/ armoede
- Slechte huisvesting
- Gebrek aan sociaal steunend netwerk van ouders
- Werkstatus van ouders
- Niet-westerse migratieachtergrond van ouders (ook grootouders)
- Thuistaal niet-Nederlands
- Beperkte etnische menging van ouders en kind (eigen kring)
- Beperkt cultureel kapitaal
- Lage ouderbetrokkenheid
- Beperkte ouderstimulering en educatieve materialen
- Beperkte kennis en vaardigheden van ouders m.b.t. (school)taal, wereldkennis, geletterdheid en wiskundig inzicht om passende inhoud te geven aan interacties met kinderen
- Beperkte kennis van ouders om succesvol te navigeren in het schoolsysteem
- Beperkte sensitieve responsiviteit, autoritaire opvoedstijl
- Beperkte ambitie van ouders
- Motivatie van ouders
- Beperkte tijd en energie van ouders
- Oriëntatie van ouders op het hier-en-nu in plaats van op de toekomst
- Weinig (gelegenheid tot) vakanties/uitjes met het gezin
Kind
- Jongen
- Aangeboren cognitieve beperkingen
- Plaats in kinderrij
- Geen eigen kamer
- Geen mobiele telefoon/Tablet/Laptop/PC in bezit
- Beperkt informatieve tv-programma’s (en programma’s in de niet-Nederlandse taal) bekijken
- Geen internetverbinding
- Beperkt aantal echte vriendjes/vriendinnetjes
- Niet deelgenomen aan VVE-programma
- Niet of beperkt deelgenomen aan (naschoolse) opvang en andere vormen van culturele socialisatie
- Niet of beperkt deelgenomen aan non-formele en informele educatie en socialisatie die privaat bekostigd wordt (schaduwonderwijs, brede sociale en culturele vorming)
- Niet of beperkte tijd doorgebracht in kinderopvang
- Doubleren
School
- Verwachtingen van en stereotypering door leerkrachten
- Gebrek aan divergente differentiatie
- Peer-learning effecten
- Groter aandeel leerlingen met een lage SES
- Groter aandeel niet-westerse achtergrond
- Hoger percentage achterstandsleerlingen op school
- Hoge mate van stedelijkheid van postcodegebied waar de school staat
- Samenloop van sociaaleconomisch zwakkere achtergronden van leerlingen op school én een groter tekort aan personeel
- Gemiddeld lager opleidingsniveau van ouders op de school
- Aandeel eenoudergezinnen
- Denominatie
Omgeving
- Minder goede leefbaarheid van wijken waarin leerlingen wonen (kwaliteit van woningen en fysieke omgeving, veiligheid)
- Lagere SES van de buurt
Bijlage 5. Resultaten expertraadpleging ronde 2
| Gezinssituatie | Aantal keer genoemd in top 10 | |
|---|---|---|
| 1. | Opleidingsniveau van ouders (met name moeder) | 5 |
| 2. | Werkstatus van ouders (werkend, uitkering, inactief) | 3 |
| 3. | Beroepssector van werkende ouders | 1 |
| 4. | Aantal kinderen in het gezin | 1 |
| 5 | Eenoudergezin | 2 |
| 6. | Leeftijd van moeder bij eerste kind | 1 |
| 7. | Gezinsinkomen (netto) | 2 |
| 8. | Eigen vermogen van het gezin | 1 |
| 9 | Betalingsachterstanden (proxy voor problematische schulden) | 1 |
| 10. | Langdurige betalingsachterstanden (proxy voor chronische financiële stress/armoede) | 3 |
| 11. | Ingrijpende levensgebeurtenissen (b.v.: verhuizing, overlijden gezinslid) | 2 |
| 12. | Familierelaties (proxy voor gebrek aan sociaal steunend netwerk) | 1 |
| 13. | Niet-westerse migratieachtergrond (ouders en grootouders) | 4 |
| 14. | Segregatie naar herkomst in sociaal netwerk (proxy voor etnische menging ouders en kind) | 0 |
| 15. | Werkuren en aantal kinderen in het gezin (proxy voor tijd en energie van ouders) | 1 |
| 16. | Verblijfsduur van de moeder in Nederland | 2 |
| Kind | Aantal keer genoemd in | |
|---|---|---|
| 1. | Geslacht | 0 |
| 2. | Plaats in de kinderrij | 1 |
| 3. | Aantal kamers in verhouding tot aantal personen in het huishouden (proxy voor het hebben van een eigen kamer) | 1 |
| 4. | Deelname aan vve-programma | 0 |
| 5. | Tijd doorgebracht in kinderopvang | 1 |
| 6. | Doubleren | 0 |
| School | Aantal keer genoemd in | |
|---|---|---|
| 1. | Gemiddeld opleidingsniveau van ouders in klas/proportie leerlingen met een lage SES in klas | 3 |
| 2. | Gemiddeld opleidingsniveau van ouders op school/proportie leerlingen met een lage SES op school | 3 |
| 3. | Proportie kinderen met een niet-westerse achtergrond op school | 1 |
| 4. | Percentage achterstandsleerlingen op school | 4 |
| 5. | Aandeel eenoudergezinnen op school | 0 |
| 6. | Stedelijkheid van het postcodegebied van school | 0 |
| 7. | Denominatie | 0 |
| 8. | Afwijking schooladvies – toetsadvies | 0 |
| Omgeving | Aantal keer genoemd in top 10 | |
|---|---|---|
| 1. | Gemiddelde SES van de buurt | 3 |
| 2. | Aandeel huishoudens onder de armoedegrens in de buurt | 4 |













