HSMR 2023 Methodological Report
About this publication
Statistics Netherlands has calculated The Hospital Standardised Mortality Ratios (HSMRs) for Dutch hospitals for the period 2021-2023. This report describes the methods that were used.
The following files are made available in the Appendix: the Excel file ‘Statistical significance of covariates HSMR 2023 model’ presents the statistical significance (95% confidence) of the covariates for the 158 logistic regressions; the Excel file ‘Classification of variables HSMR 2023’ contains the classifications used for the diagnosis groups, severity of main diagnosis, socio-economic status and source of admission and; the Excel file ‘Coefficients HSMR 2023’ contains the coefficients and standard errors of the HSMR model by diagnosis group.
In chapter 2 the changes compared to previous HSMR calculations are described. Chapter 3 describes the HSMR model methods and in chapter 4 the quality of the present HSMR model is evaluated.
HSMR 2023 outcomes are published by the hospitals (31 December 2024 at the latest), on the websites of the individual hospitals.
1. Introduction
This report presents the methods Statistics Netherlands (CBS) has used to calculate the Hospital Standardised Mortality Ratios (HSMRs) for Dutch hospitals. HSMRs are ratios of observed and expected numbers of deaths and aim to present in-hospital mortality figures in comparison to the national average. This chapter gives a general overview of the HSMR. Chapter 2 presents the changes introduced in the method of calculating the HSMR. The methodological aspects of the model used to calculate the HSMRs are described in chapter 3. The model outcomes are evaluated in chapter 4. Conclusions are given in chapter 5.
1.1 What is the (H)SMR?
In-hospital mortality can be measured as the ratio of the number of hospital deaths to the number of hospital admissions (hospital stays) in the same period. This is generally referred to as the “gross mortality rate”. Judging hospital performance on the basis of gross mortality rates is unfair, since one hospital may have had more life-threatening cases than another. Therefore it is more appropriate to adjust (i.e. standardise) mortality rates for differences in patient characteristics (”case mix”) across hospitals as much as possible. To this end, the SMR (Standardised Mortality Ratio) of a hospital h for diagnosis d is defined as
The numerator is the observed number of deaths with main diagnosis d in hospital h. The denominator is the expected number of deaths for this type of admission under the assumption that individual mortality probabilities (per admission) do not depend on the hospital, i.e. are equal to mortality probabilities of identical cases in other hospitals. The denominator is determined using a model based on data from all national hospitals, in which the in-hospital mortality is explained by patient characteristics, such as age and diagnosis, and characteristics of the admission, such as whether the admission is acute or not. Characteristics of the hospital, such as the number of doctors per bed, are generally not incorporated in the model, since these can be related to the quality of care which is the intended outcome of the indicator. The model thus produces an expected (estimated) mortality probability for each admission. Adding up these probabilities per hospital gives the total expected mortality over all admissions of that hospital. For each diagnosis d, the average SMRd across all hospitals equals 100 when each hospital is weighted with its (relative) expected mortality.
The HSMR of hospital h is defined as
in which both the numerator and denominator are sums across all admissions for all considered diagnoses. The HSMR thus also has a weighted average of 100. As HSMRs may also deviate from 100 by chance only, confidence intervals are calculated for the SMRs and HSMRs to inform hospitals whether they have a (statistically) significantly high or low adjusted mortality rate compared with the average value of 100.
1.2 Purpose of the HSMR
As in many other countries, there is much interest in measuring the quality of health care in the Netherlands. Various quality indicators are available, such as the number of medical staff per bed or the availability of certain facilities. However, these indicators do not measure the outcomes of medical performance. A good indicator for the performance of a hospital is the extent to which its patients recover, given the diagnoses and other important patient characteristics, such as age, sex and comorbidity. Unfortunately, recovery is hard to measure and mostly occurs after patients have been discharged from the hospital. Although in-hospital mortality is a much more limited quality indicator, it can be measured accurately and is therefore used as a quality indicator in several countries, using the HSMR and SMRs as defined in section 1.1. If these instruments were totally valid, i.e. the calculations would adjust perfectly for everything that cannot be influenced by the hospital, a value above 100 would always indicate inferior quality of care, and the difference between numerator and denominator could be considered an estimate of “avoidable mortality”. This would only be possible if the measurement was perfect and mortality by unforeseeable complications was equally distributed across hospitals, after adjustment for differences in case mix. However, it is impossible to construct such a perfect instrument to measure the quality of health care; the outcome of the indicator will to some extent always be partially influenced by differences between hospitals with regard to case mix, availability of highly specialized treatment options, etc. A significantly high (H)SMR will at most be an indication of possible shortcomings in hospital care, but a high value may also be caused by coding errors in the data or a lack of essential covariates related to mortality in the model. Still, a significantly high (H)SMR is often seen as a warning sign and a reason for further investigation by the hospital.
1.3 History of the HSMR
In 1999 Jarman initiated the calculation of the (H)SMR for hospitals in England (Jarman et al., 1999). In the following years the model for estimating mortality probabilities was improved by incorporating additional covariates. Analogous models were adopted by some other countries.
In 2005, Jarman started to calculate the (H)SMR for the Netherlands. Later on, these Dutch (H)SMRs were calculated by Kiwa Prismant, in collaboration with Jarman and his colleagues of Imperial College London, Dr Foster Intelligence in London and De Praktijk Index in the Netherlands. Their method, described in Jarman et al. (2010), was slightly adapted by Prismant (Prismant, 2008) up to reporting year 2009. In 2010 DHD (Dutch Hospital Data, Utrecht), the registry holder of the national hospital discharge data, asked CBS to calculate the (H)SMRs for the period 2008-2010 and for subsequent years. CBS is an independent public body and is familiar with the input data for the HSMR, i.e. the hospital discharge register (LBZ: Landelijke Basisregistratie Ziekenhuiszorg and its predecessor LMR: Landelijke Medische Registratie), as it uses this data source for a number of health statistics (see https://opendata.cbs.nl/statline/#/CBS/nl/navigatieScherm/thema?themaNr=82174).
The starting point for CBS was the HSMR method previously used by Prismant. As a result of progressive insight, over the years CBS has introduced changes in the model for the HSMR, which are described in the annual methodological reports (CBS, 2011, 2012, 2013, etc.).
1.4 Confidentiality
Under the Statistics Netherlands Act, CBS is required to keep all data about individuals, households, companies or institutions confidential. Therefore it normally does not deliver recognisable data from institutions to third parties, unless the institutions concerned explicitly agree. For this reason, CBS needs written consent from all hospitals to deliver their hospital-specific (H)SMR figures to DHD. CBS only supplies DHD with (H)SMR outcomes of hospitals that have granted authorisation to do so. In turn, DHD sends each hospital its individual outcome report. Publication of (H)SMR data, which has become mandatory in the Netherlands since 2014 by a regulation of the Dutch Healthcare Authority (NZa), is the responsibility of the hospitals themselves. CBS does not publish data on identifiable hospitals.
1.5 CBS output
CBS annually estimates the models for expected mortality per diagnosis for the most recent three-year period. It calculates the HSMRs and SMRs for all hospitals that (1) had authorised CBS, (2) had registered all of its admissions in the LBZ in the relevant period, and (3) were not excluded on the grounds of criteria for data quality and comparability, which means that the hospital’s LBZ data were not too deviant in some respects (see section 3.5).
CBS produces the following output:
- Individual hospital reports, containing their HSMR and diagnosis-specific SMR figures for the most recent reporting year and the three-year period. SMRs are also presented for different patient groups (by age, sex and urgency of admission) and for clusters of diagnoses. Hospitals can compare their outcome with the national average: overall, and per diagnosis and patient group.
- A dataset for each hospital with the mortality probabilities for all its individual admissions. Besides the mortality probability, each admission record contains the observed mortality (0 or 1) and the scores on the covariates of the HSMR model. Hospitals can use these data for internal investigation.
- A report on the methods used for calculating the HSMR, including the model results and parameters (this document; see www.cbs.nl).
1.6 Limitations of the HSMR
In section 1.2 we argued that the HSMR is not the only indicator to measure quality of hospital care. Furthermore, the quality and limitations of the HSMR (and the SMR) instrument are under debate. After all it is based on a statistical model (i.e. the denominator), which is always a simplification of reality.
Since the very first publication on the HSMR in the United Kingdom, there has been an on-going debate about the value of the HSMR as an instrument. Supporters and opponents agree that the HSMR is not a unique, ideal measure, but at most a possible indicator of the quality of health care, alongside other possible indicators. But even if HSMRs were to be used for a more limited purpose, i.e. standardising in-hospital mortality rates for unwanted side-effects, the interpretation of HSMRs would present various problems, some of which are described briefly below. See also Van Gestel et al. (2012) for an overview.
- Section 3.4 contains the list of covariates included in the regression model. Hospitals do not always code these variables in the same way. Variables such as age and sex are registered uniformly, but the registration of whether an admission was acute or not, the main discharge diagnosis or comorbidity may depend on individual physicians and coders. Lilford and Pronovost (2010) argue that if the quality of the source data is insufficient, the regression model should not adjust for such erroneously coded covariates. Our own research (Van der Laan, 2013) shows that comorbidities in particular present a problem in the Netherlands, as there is large variation in coding of this covariate (see also section 4.3). Van den Bosch et al. (2010) refer extensively to the influence of coding errors and Van Erven et al. (2018) also describe underreporting of comorbidities. Nationwide, the registration of comorbidities in Dutch hospitals has increased strongly up to 2014. From 2015 onwards the yearly increase is smaller, and in 2021 the registration of comorbidities seemed to stabilize. However, there are still hospitals with annual shifts in the registration of comorbidities. Exclusion criteria for outliers may solve this problem partly but not completely.
- Another problem is that some hospitals do not sufficiently register whether a comorbidity was a complication or not. As complications are excluded from the HSMR comorbidity covariates, underreporting complications might falsely lead to a higher comorbidity rate, thus influencing the HSMR outcomes. To stimulate correct coding of in-hospital complications, an indicator has been added to the hospital HSMR reports showing the percentage of conditions not present on admission (not POA) in a hospital, and the overall average. The introduction of this indicator has led to less underreporting of conditions not POA, though there are still differences in the number of not POA registrations by hospitals.
- Some hospitals may, on average, treat more seriously ill patients than others, even if those patients have the same set of scores on the covariates. University hospitals may, for example, have more complicated cases than other hospitals, while regional hospitals are generally more involved in end of life care. It is questionable whether the model sufficiently adjusts for factors such as severity and complexity of disease. As some of the desired covariates, such as disease stage, are not registered in the LBZ and may actually be hard to measure at all in this type of registry with routinely collected hospital discharge data, essential information to correct for differences in case mix between hospitals may be missing.
- A similar problem occurs when certain high-risk surgical procedures are only performed in a selection of hospitals. For instance, open heart surgery only occurs in authorised cardiac centres, and these hospitals may have higher SMRs for heart disease because they perform such risky interventions. This could be solved by including a covariate in the model that indicates whether such a procedure was performed. The downside however, of using a treatment method as a covariate, is that ideally it should not be part of the model as it is a component of hospital care.
- Hospital admission and discharge policies may differ between hospitals. For instance, one hospital may admit the same patient more frequently but for shorter stays than another. Or it may discharge a patient earlier due to higher availability of external terminal care facilities in the neighbourhood. Also, patients may be referred from one hospital to another for further treatment. Obviously, all these situations that mostly are unrelated to quality of care influence the observed mortality numbers and thereby the outcome of the HSMR.
- Hospitals can compare their HSMR and SMRs with the national average value of 100. A comparison of (H)SMRs between two (or more) hospitals is more complicated, as there is no complete adjustment for differences in case mix between pairs of hospitals. Theoretically, it is even possible that hospital A has higher SMRs than hospital B for all diagnosis groups, but a lower HSMR. Although this is rather theoretical, bilateral comparison of HSMRs should be undertaken with caution (Heijink et al., 2008).
Some issues in the incomplete correction for differences in case mix between hospitals may be partly addressed by peer group comparison of (H)SMRs. The calculation of (H)SMRs is still based on the model for all hospitals (without correcting for the type of hospital), but peer group comparison allows a specialised hospital to compare its results with the average for similar hospitals. For instance, the average HSMR of university hospitals is >100 in the Netherlands due to insufficient case mix correction, but comparing their results with a peer group average allows these hospitals (and for specific diagnoses also other specialised hospitals) to better interpret their own scores.
To tackle the problem relating to differences in discharge policies (e.g. the availability of terminal care outside hospital), and to some extent referrals between hospitals, an indicator of early post-discharge mortality could be included, in addition to in-hospital mortality. Ploemacher et al. (2013) observed a decrease in standardised in-hospital mortality in the Netherlands in 2005-2010, which may have been caused by an overall improvement in quality of care, but may also be partly explained by substitution of in-hospital mortality by outside-hospital mortality, possibly caused by changes in hospital admission and discharge policies. Pouw et al. (2013) performed a retrospective analysis on Dutch hospital data linked to mortality data, and concluded that including early post-discharge mortality diminishes the effect of discharge bias on the HSMR. In the UK, the SHMI (Summary Hospital-level Mortality Indicator) has been adopted, which includes mortality up to 30 days after discharge (Campbell et al., 2011). In 2014, CBS studied the optimal time frame and definition of an indicator including early post-discharge mortality (Van der Laan et al., 2015). Including all mortality within a 45-day period after admission was advised to reduce the influence of hospital discharge policies on the HSMR. A French study also recommended fixed post-admission periods of more than 30 days (Lamarche-Vadel et al., 2015).
However, including post-discharge mortality in the indicator will not reduce the effect of differences in admission policies for terminally ill patients. Some hospitals may admit more terminally ill patients to provide terminal palliative care than other hospitals and those admissions may distort HSMR outcomes. Unfortunately, an international definition for palliative care in general is lacking and definitions are therefore not uniformly or consistently applied. Palliative care can be registered with ICD-10 code Z51.5, but this variable should be used with caution, as differences between hospitals in coding practices are likely and have already been shown in the UK and Canada (NHS, 2013; Chong et al., 2012; Bottle et al., 2011). Alternatively, in the Netherlands, procedure codes (‘Zorgactiviteiten’) 190006, 190067 (introduced in 2018) and 190173 (code introduced in 2023 for palliative care for children) can be used as palliative care indicators. These procedure codes are used to register a meeting regarding palliative care or a consult by a palliative care team member. As the Dutch Healthcare Authority has formulated guidelines for registration of palliative care using these procedure codes, it is more likely that these are more uniformly applied between hospitals within the Netherlands. Using procedure codes rather than ICD-10 codes as palliative care indicators is also preferable considering the LBZ coding guidelines which prescribe that ICD-10 codes should not be used to register care when a procedure code has already been used to register that same care. Nevertheless, considerable differences between hospitals regarding consultation of a palliative care team and the registration of palliative care using procedure codes may still exist. Additionally, neither ICD-10 nor procedure codes distinguish between early and terminal palliative care, and adjusting the HSMR for palliative care may increase the risk of gaming (NHS, 2013; Chong et al., 2012). Palliative care admissions have therefore not yet been excluded from the calculation of the HSMR in the Netherlands. However, the hospital HSMR reports include information on the percentage of the hospital’s admissions and deaths related to palliative care as registered in the LBZ compared to the overall average. This may indicate to some extent whether or not palliative care could have biased a hospital’s HSMR. From the HSMR 2023 onwards (applied to all years of the present reporting period), the procedure codes will be used as a palliative care indicator instead of the ICD-10 code Z51.5 (see section 2.1).
Despite the above-mentioned limitations and the ongoing debate on the validity and reliability of mortality-based indicators like the HSMR, there are studies that suggest that mortality monitoring can be indicative of failings in quality of care. In an English hospital setting, Cecil et al. (2020) found that mortality alerts, based on higher than expected mortality in 122 diagnosis and procedure groups, were associated with structural indicators of lower quality of care (e.g. lower nurse-to-bed ratio, overcrowding and financial pressures) and outcome indicators like lower patient and trainee satisfaction. They conclude that a mortality alerting system might be valuable in highlighting poor quality of care.
2. Method changes
This chapter summarizes the changes in the HSMR method (HSMR 2023) compared to the method used last year (HSMR 2022).
For previous changes see the respective methodological reports (CBS, 2011, …, 2023). Overall, the method has
remained the same.
Since last year (HSMR 2022) COVID-19 admissions from 2022 onwards are included in the HSMR model using a specific
COVID-19 SMR model with different definitions of covariates “Severity of the main diagnosis” and
“Month of admission” (see section 3.4). This year the same COVID-19 SMR model is used as last year, but
now also includes covariate “Year of discharge”, as COVID-admissions of two years (2022 and 2023) are
now included. COVID-19 admissions in 2021 are still excluded. The three-year COVID-19 SMR therefore only includes
COVID-19 admissions from 2022-2023.
This year only a few changes related to the indicators used for data quality and case mix have been implemented.
These indicators are not used in the HSMR model, but serve as background information for the hospitals (see also
section 1.6). The changes in these indicators are described below and are applied to all years of the present
reporting period (2021-2023):
Indicators of palliative care:
Palliative care was previously measured with ICD-10 code Z51.5. However, this approach has limitations, see section 1.6. Therefore it is now measured using procedure codes (‘Zorgactiviteiten’) 19006, 190067 and 190173. These codes are registered when a meeting regarding palliative care or a consult by a palliative care team member has taken place during the hospital admission.
Indicator of the registration of secondary diagnoses:
In the calculation of the indicator “average number of registered secondary diagnoses per admission” supplementary diagnosis codes indicating external causes, morphology and the type of bacteria in case of an infection, are now excluded. This concerns ICD-10 codes B95-B98, U80-U85, codes starting with V, W, X or Y and morphology codes. These codes are registered supplementary to codes representing diagnoses such as injury, neoplasms and infections and do not represent a separate condition.
Indicator of the registration of complications:
In the calculation of the indicator ”percentage of registered diagnoses not present on admission (not POA)” apart from the above-mentioned supplementary diagnosis codes, Z-codes that do not indicate a condition are now also excluded. In total the following ICD-10 codes are thus excluded in this indicator: B95-B98, U80-U85, codes starting with V, W, X or Y, morphology codes, and (in the numerator only) all Z-codes except Z04.3 and Z20.
3. (H)SMR model
Expected in-hospital mortality - i.e. the denominator of the SMR - has to be determined for each diagnosis group. To this end we use logistic regression models, with mortality as the target (dependent) variable and various variables available in the LBZ as covariates. The regression models to calculate the (H)SMR of a three-year period (year t-2 up to year t), and the (H)SMRs of the individual years t-2, t-1 and t, are based on LBZ data of four years: year t-3 up to year t. The addition of an additional year (t-3) increases the stability and accuracy of the estimates, while the moving four-year period up to year t keeps the model up to date.
3.1 Target population and dataset
3.1.1 Hospitals
“Hospital” is the primary observation unit. Hospitals register data on admissions (hospital stay data) in the LBZ. However, not all hospitals participate in the LBZ. In principle, the HSMR model includes all short-stay hospitals with inpatient admissions participating in the LBZ in the relevant years. The target population of hospitals that qualify for entry in the HSMR model thus includes all general hospitals, all university hospitals, and short-stay specialised hospitals with inpatient admissions that participate in the LBZ. In case of partial non-response by hospitals, only the fully registered months are included in the model, as in the other months fatal cases might be registered completely and non-fatal cases partially. The partially registered months of those hospitals are removed from the model as these might otherwise unjustly influence the estimates. In addition, if for any reason registered data of hospitals in a specific LBZ year had not been not validated by DHD, that year of data is not included in the HSMR model.
All of the above-mentioned hospitals were included in the model. Data of a short-stay specialised hospital that started registering data in the LBZ in 2022 were also included. (H)SMRs were only calculated for hospitals that met the criteria for LBZ participation, data quality and case mix (see section 3.5).
3.1.2 Admissions
In addition to the population of hospitals, the population of admissions is considered. Our target population of admissions consists of all hospital stays (i.e. inpatient admissions, and prolonged observations, unplanned, without overnight stay) of Dutch residents in Dutch hospitals in a certain period, except admissions that do not meet the billing criteria of the Dutch Healthcare Authority for inpatient admissions, prolonged observations, and admissions of healthy persons, such as healthy newborns, healthy parents accompanying sick children, or other healthy boarders. The date of discharge, and not the day of admission, determines the year a record is assigned to. So the population of hospital stays of year t comprises all admissions that ended in year t. For the sake of convenience mostly we call these hospital stays “admissions”, thus meaning the hospital stay instead of only its beginning. Day admissions are excluded as these are in principle non-life-threatening cases with hardly any mortality. However, from 2015 onwards the new case type “prolonged observations, unplanned, without overnight stay” is included in the HSMR. This case type was introduced by the Dutch Healthcare Authority (NZa), and replaces the majority of the acute one-day inpatient admissions that had formerly been registered. It involves more mortality than day cases, and it is therefore relevant to include this case type in the HSMR.
Admissions that do not meet the billing criteria of the Dutch Healthcare Authority are removed from the data in all consecutive model years. This primarily concerns one-day inpatient admissions where the patient returned home after discharge. Also, over a hundred in-hospital deaths where the patient was admitted after 20:00 hrs. and died before 24:00 hrs. on the same day, were removed from the dataset.
Admissions of healthy persons are additionally removed. These admissions are identified by the main diagnosis of the admission (ICD-10 code Z76.2-Z76.4) and/or the registration of procedure codes for a stay of a healthy newborn or healthy mother for each individual day of the admission (Dutch procedure codes 190032, 190033 (‘Zorgactiviteiten’ codes), 339911 or 339912 (‘CBV’ codes)).
For the years 2020 and 2021 all admissions with COVID-19 as the principal diagnosis (ICD-10 codes U07.1 (COVID-19, virus identified (lab confirmed)), U07.2 (COVID-19, virus not identified (clinically diagnosed)) and U10.9 (Multisystem inflammatory syndrome associated with COVID-19, unspecified)) were removed from the dataset.
Lastly, admissions of foreigners are excluded from the HSMR model, partly in the context of possible future modifications of the model, when other data can be linked to admissions of Dutch residents. The number of admissions of foreigners is relatively small.
3.2 Target variable (dependent variable)
3.3 Stratification
Instead of performing one logistic regression for all admissions, we performed a separate logistic regression for each of the diagnosis groups d. These sub-populations of admissions are more homogeneous than the entire population. Hence, this stratification may improve the precision of the estimated mortality probabilities. As a result of the stratification, covariates are allowed to have different regression coefficients across diagnosis groups.
The diagnosis groups are clusters of ICD codes registered in the LBZ. Here the main diagnosis of the admission is used, i.e. the main reason for the hospital stay, which is determined at discharge. The basis for the clustering is the CCS (Clinical Classifications Software1)), which clusters ICD diagnoses into 259 clinically meaningful categories. The COVID-19 admissions were arbitrarily assigned to group number 260, although this group is originally assigned to external causes of disease by the Clinical Classifications Software. But since external causes of disease cannot be registered as main diagnosis (only as secondary diagnosis) in the LBZ this does not cause any conflict in the data. For the HSMR, we further clustered these 260 categories into 158 diagnosis groups (where group nr. 158 consists of the COVID-19 admissions), which are partly the same clusters used for the SHMI (Summary Hospital-level Mortality Indicator) in the UK (HSCIC, 2016). Therefore, the model includes 158 separate logistic regressions, one for each diagnosis group d selected.
In the file “Classification of variables”, published together with this report, for each of the 158 diagnosis groups the corresponding CCS group(s) are given, as well as the ICD-10 codes of each CCS group.
Apart from the SMRs for each of the 158 diagnosis groups, hospitals also receive SMRs for 17 aggregates of diagnosis groups. This allows the evaluation of SMR outcomes at both the detailed and the aggregated diagnosis level. The 17 main clusters are also given in the “Classification of variables” file. These were derived from the main clusters in the CCS classification of HCUP, with the following adaptations:
- HCUP main clusters 17 (“Symptoms; signs; and ill-defined conditions and factors influencing health status”) and 18 (“Residual codes; unclassified”) were merged into one cluster.
- CCS group 54 (“Gout and other crystal arthropathies”) is classified in main cluster “Diseases of the musculoskeletal system and connective tissue”, and CCS group 57 (“Immunity disorders”) is classified in main cluster “Diseases of the blood and blood-forming organs”, whereas in the HCUP classification these groups fall in main cluster “Endocrine, nutritional and metabolic diseases, and immunity disorders”.
- CCS group 113 (“Late effects of cerebrovascular disease”) is classified in main cluster “Diseases of the nervous system and sense organs”, whereas in the HCUP classification this group falls in main cluster “Diseases of the circulatory system”.
- CCS group 218 (“Liveborn”) is classified in main cluster “Complications of pregnancy, childbirth, and the puerperium; liveborn”, whereas in the HCUP classification this group falls in main cluster “Certain conditions originating in the perinatal period”.
- COVID-19 (group 158) was added to the main cluster “Infectious and parasitic diseases”.
These adaptations are in accordance with the diagnosis groups used for the SHMI (Summary Hospital-level Mortality Indicator) in the United Kingdom (HSCIC, 2016).
Although the names of the main clusters are quite similar to the names of the chapters of the ICD-10, there is no one-to-one relation between the two. Although most ICD-10 codes of a CCS group do fall within one ICD-10 chapter, often some of the codes are categorised in other chapters. Especially the codes from the R chapter of ICD-10 are scattered over several HCUP main clusters.
3.4 Covariates (explanatory variables or predictors of in-hospital mortality)
By including covariates of patient and admission characteristics in the model, the in-hospital mortality and thus the (H)SMRs are adjusted for these characteristics. Thus, variables (available in the LBZ) associated with patient in-hospital mortality are chosen as covariates. The more the covariates discriminate between hospitals, the larger the effect on the (H)SMR.
The LBZ variables that are included in the model as covariates are age, sex, socioeconomic status, severity of the main diagnosis, urgency of admission, Charlson comorbidities, source of admission, year of discharge and month of admission. These variables are described below. Detailed classifications of the variables socioeconomic status, severity of the main diagnosis and source of admission are provided in the file “Classification of variables”, published together with this report.
For the regressions, all categorical covariates are transformed into dummy variables (indicator variables), having scores of 0 or 1. A patient scores 1 on a dummy variable if he/she belongs to the corresponding category, and 0 otherwise. As the dummy variables for a covariate are linearly dependent, one dummy variable is left out for each categorical covariate. The corresponding category is the so-called reference category. We took the first category of each covariate as the reference category.
The general procedure for collapsing categories is described in section 3.6.2. Special (deviant) cases of collapsing are mentioned below.
Age at admission (in years):
- 0, 1-4, 5-9, 10-14, …, 90-94, 95+.
Sex of the patient:
- male, female.
If Sex is unknown, “female” was imputed. This is a rare occurrence.
SES (socioeconomic status) of the postal area of patient’s home address:
- lowest, below average, average, above average, highest, unknown.
The SES variable was added to the LBZ dataset on the basis of the postal code of the patient’s residence, as
registered in the LBZ. The SES classification is derived from the so called ‘SES-WOA’ scores calculated
by Statistics Netherlands (Arts et al., 2022). This SES-WOA score is based on household data concerning welfare (a
combination of income and wealth), level of education and recent labour participation. The scores are determined at
the household level and then averaged to scores per four-digit postal code. Household-weighted quintiles were
calculated from these scores, resulting in the six SES categories mentioned above. Patients for whom the postal area
does not exist in the dataset (category “unknown”), were added to the category “average” if
collapsing was necessary.
For the HSMR model years 2020-and 2021 the SES-WOA scores of 2019 calculated by Statistics Netherlands were used and
for model years 2022 and 2023 the SES-WOA scores of 2021 were used.
Severity of the main diagnosis groups:
- [0-0.01), [0.01-0.02), [0.02-0.05), [0.05-0.1), [0.1-0.2), [0.2-0.3), [0.3-0.4), [0.4-1], Other.
COVID-19_ subdiagnosis:
(for diagnosis group 158 (COVID-19), instead of ‘Severity of the main diagnosis’)
- U07.1, U07.2, U10.9
The ”Severity of the main diagnosis” covariate is a categorisation of main diagnoses into mortality rates. For the diagnosis groups 1-157, each ICD-10 main diagnosis code is classified in one of these groups, as explained below.
Most of the diagnosis groups have many subdiagnoses (individual ICD-10 codes), which may differ in severity (mortality risk). To classify the severity of the subdiagnoses, we used the method suggested by Van den Bosch et al. (2011), who suggested categorising the ICD codes into mortality rate categories. To this end, we computed inpatient mortality rates for all occurring ICD subdiagnoses of the admissions in the current model years, using data of six historical LBZ years, and chose the following boundaries for the mortality rate intervals: 0, .01, .02, .05, .1, .2, .3, .4 and 1. (“0” means 0 percent mortality; “1” means 100 percent mortality). These boundaries are used for all individual ICD codes. The higher severity categories only occur in a few diagnosis groups. Six historical LBZ years are used to determine this classification, not overlapping with the years the HSMR is calculated for as otherwise both are using the same mortality data. The period of the historical dataset shifts every year for each new HSMR calculation, to keep it up to date.
For newly added ICD-10 codes in recent years a converted “old” ICD-10 code (code used for the disease prior to the introduction of the new ICD-10 code) was determined, in consultation with DHD. If such an ICD-10 code did not occur in the historical dataset, a severity of ”other” was assigned in the calculation of the (H)SMR. ICD codes that are used by less than four hospitals and/or have less than 20 admissions were also set to ”other”. The category ”other” contains diagnoses for which it is not possible to accurately determine the severity. However, if this category “other” needs to be collapsed (see section 3.6.2), it does not have a natural nearby category. We decided to collapse “other” with the category with the highest frequency (i.e. the mode), if necessary. In the file with regression coefficients (see section 4.5) this will result in a coefficient for “other” equal to that of the category with which “other” is collapsed. The only exceptions are when Comorbidity 17 (Severe liver disease) is collapsed with Comorbidity 9 (Liver disease), and when Comorbidity 11 (Diabetes complications) is collapsed with Comorbidity 10 (Diabetes). In these cases the regression coefficient of Comorbidity 17/11 is set to zero in the coefficients file, and the coefficient of the less severe analogue (Comorbidity 9/11) should be used for Comorbidity 17/11.
The individual ICD-10 codes with the corresponding severity categories are available in the separate file “Classification of variables”, published together with this report.
Urgency of the admission
- elective, acute.
The definition of an acute admission is: an admission that cannot be postponed, as immediate medical treatment or aid within 24 hours is necessary. Within 24 hours means 24 hours from the moment the specialist decides that acute admission is necessary.
Comorbidity 1 – Comorbidity 17.
- All these 17 covariates are dummy variables, having categories: 0 (no) and 1 (yes).
The 17 comorbidity groups are listed in table 3.4.1, with their corresponding ICD-10 codes. These are the same comorbidity groups as in the Charlson index. However, separate dummy variable are used for each of the 17 comorbidity groups.
All secondary diagnoses registered in the LBZ and belonging to the 17 comorbidity groups are used, but if the ICD-10 code of a secondary diagnosis is identical to that of the main diagnosis, it is not considered a comorbidity. Secondary diagnoses registered as not present on admission (not POA) are not counted as a comorbidity either.
In conformity with the collapsing procedure for other covariates (see section 3.6.2), comorbidity groups registered in fewer than 50 admissions or that have no deaths are left out, as the two categories of the dummy variable are then collapsed. An exception was made for Comorbidity 17 (Severe liver disease) and Comorbidity 11 (Diabetes complications). Instead of leaving out these covariates in the case of fewer than 50 admissions or no deaths, they are first added to the less severe analogues Comorbidity 9 (Liver diseases) and Comorbidity 10 (Diabetes), respectively. If the combined comorbidities still have fewer than 50 admissions or no deaths, then these are dropped after all.
The ICD-10 definitions listed in table 3.4.1 are mostly identical or nearly identical to those of Quan et al. (2005), with some adaptations, which are described in CBS (2014). Furthermore, newly introduced ICD-10 codes have been added by CBS if the corresponding ‘old’ ICD-10 code is part of a comorbidity group.
3.4.1 Comorbidity groups of Charlson index and the corresponding ICD-10 codes
No. Comorbidity groups ICD-10 codes 1 Myocardial infarction I21, I22, I25.2 2 Congestive heart failure and cardiomyopathy I50, I11.0, I13.0, I13.2, I25.5, I42, I43, P29.0 3 Peripheral vascular disease I70, I71, I73.1, I73.8, I73.9, I77.1, I79.0, I79.2, K55.1, K55.8, K55.9, Z95.8, Z95.9, R02, Z99.4 4 Cerebrovascular disease G45.0-G45.2, G45.4, G45.8, G45.9, G46, I60-I69 5 Dementia F00-F03, F05.1, G30, G31.1 6 Pulmonary disease J40-J47, J60-J67 7 Connective tissue disorder M05, M06.0, M06.3, M06.9, M32, M33.2, M34, M35.3 8 Peptic ulcer K25-K28 9 Liver disease B18, K70.0-K70.3, K70.9, K71.3-K71.5, K71.7, K73, K74, K76.0, K76.2-K76.4, K76.8, K76.9, Z94.4 10 Diabetes E10.9, E11.9, E12.9, E13.9, E14.9 11 Diabetes complications E10.0-E10.8, E11.0-E11.8, E12.0-E12.8, E13.0-E13.8, E14.0-E14.8 12 Hemiplegia or paraplegia G04.1, G11.4, G80.1, G80.2, G81, G82, G83.0-G83.5, G83.8, G83.9 13 Renal disease I12.0, I13.1, N01, N03, N05.2-N05.7, N18, N19, N25, Z49.0-Z49.2, Z94.0, Z99.2 14 Cancer C00-C26, C30-C34, C37-C41, C43, C45-C58, C60-C76, C81-C85, C86.0-C86.6, C88, C90-C97, D47.5 15 HIV B20-B24, O98.7 16 Metastatic cancer C77-C80 17 Severe liver disease I85.0, I85.9, I86.4, I98.2, I98.3, K70.4, K71.1, K72.1, K72.9, K76.5, K76.6, K76.7
| No. | Comorbidity groups | ICD-10 codes |
|---|---|---|
| 1 | Myocardial infarction | I21, I22, I25.2 |
| 2 | Congestive heart failure and cardiomyopathy | I50, I11.0, I13.0, I13.2, I25.5, I42, I43, P29.0 |
| 3 | Peripheral vascular disease | I70, I71, I73.1, I73.8, I73.9, I77.1, I79.0, I79.2, K55.1, K55.8, K55.9, Z95.8, Z95.9, R02, Z99.4 |
| 4 | Cerebrovascular disease | G45.0-G45.2, G45.4, G45.8, G45.9, G46, I60-I69 |
| 5 | Dementia | F00-F03, F05.1, G30, G31.1 |
| 6 | Pulmonary disease | J40-J47, J60-J67 |
| 7 | Connective tissue disorder | M05, M06.0, M06.3, M06.9, M32, M33.2, M34, M35.3 |
| 8 | Peptic ulcer | K25-K28 |
| 9 | Liver disease | B18, K70.0-K70.3, K70.9, K71.3-K71.5, K71.7, K73, K74, K76.0, K76.2-K76.4, K76.8, K76.9, Z94.4 |
| 10 | Diabetes | E10.9, E11.9, E12.9, E13.9, E14.9 |
| 11 | Diabetes complications | E10.0-E10.8, E11.0-E11.8, E12.0-E12.8, E13.0-E13.8, E14.0-E14.8 |
| 12 | Hemiplegia or paraplegia | G04.1, G11.4, G80.1, G80.2, G81, G82, G83.0-G83.5, G83.8, G83.9 |
| 13 | Renal disease | I12.0, I13.1, N01, N03, N05.2-N05.7, N18, N19, N25, Z49.0-Z49.2, Z94.0, Z99.2 |
| 14 | Cancer | C00-C26, C30-C34, C37-C41, C43, C45-C58, C60-C76, C81-C85, C86.0-C86.6, C88, C90-C97, D47.5 |
| 15 | HIV | B20-B24, O98.7 |
| 16 | Metastatic cancer | C77-C80 |
| 17 | Severe liver disease | I85.0, I85.9, I86.4, I98.2, I98.3, K70.4, K71.1, K72.1, K72.9, K76.5, K76.6, K76.7 |
Source of admission:
- home, nursing home or other institution, (other) hospital.
This variable indicates the patient’s location before admission.
Year of discharge:
- 2020, 2021, 2022, 2023.
Inclusion of the year of discharge guarantees that the total number of observed and expected (predicted) deaths are equal for that year. As a result the yearly (H)SMRs have an average of 100 when weighting the hospitals proportional to their expected mortality.
Month of admission:
- For diagnosis groups 1-157 there are 6 categories:
January/February, …, November/December. - For diagnosis group 158 (COVID-19) there are 13 categories:
0-before Year of discharge, 1-January, 2-February, …, 12-December.
For diagnosis groups 1-157 the months of admission are combined into 2-month periods. As was done previous year, a more detailed variant of month of admission is used for the COVID-19 diagnosis group (nr. 158), consisting of 13 values: one for each individual month and a separate category ‘before Year of discharge’ for admissions that started in the calendar year prior to the year of discharge. This more detailed variable allows the COVID-19 model to more distinctly adjust for the effects of different transmission waves. For example, admissions that started in November 2023 and ended in December 2023 (Month of admission ‘November’; Year of discharge ‘2023’) are thus distinguished from admissions that started in November 2022 and ended in January 2023 (Month of admission ‘Before Year of discharge’, Year of discharge ‘2023’). These admissions with the same year of discharge would otherwise fall in the same category of Month of admission (‘November’ in this example). However, as the HSMR is calculated using additive models (without interactions), the present two year’s COVID-19 model with month of admission and year of discharge does not capture all of the differences between COVID-19 waves in 2022 and 2023 (the months at which they occurred differ and the COVID-19 variants differ). Furthermore, a disadvantage of using the category ‘Before Year of discharge’ in the month of admission covariate is that this implicitly includes information on the length of the hospital stay, as this category can only be encoded for admissions that start in one month and end in a later month. This is undesirable as in principle we only want to correct for characteristics at the moment of admission. It was decided to only investigate a different method of handling month of admission in case this year’s COVID-19 model quality would have significantly deteriorated compared to last year’s COVID-19 model, which was not the case (see section 4.4). Therefore, we did not change the COVID-19 model.
3.5 Exclusion criteria
Although all hospitals mentioned in section 3.1.1 are included in the model, HSMR outcome data were not produced for
all hospitals. HSMRs were only calculated for hospitals that met the criteria for LBZ participation, data quality
and case mix. In addition to this, only HSMRs were calculated for hospitals that had authorised CBS to supply their
HSMR figures to DHD.
The criteria for excluding a hospital from calculating HSMRs, based on the characteristics of the registered
inpatient admissions and prolonged observations without overnight stay, were:
Insufficient participation in the LBZ
- Hospitals are excluded if they do not register all inpatient admissions and “prolonged observations, unplanned, without overnight stay” that meet the billing criteria of the Dutch Healthcare Authority (NZa) in the LBZ.
Data quality
Hospitals are excluded if:
- ≤30% of admissions are coded as acute.
- ≤1.5 secondary diagnoses are registered per admission, on average per hospital2).
Case mix
Hospitals are excluded if:
- Observed mortality is less than 60 in all registered admissions.
Admissions in 2021 with COVID-19 as main diagnosis were excluded from the dataset that was used to calculate the outcomes of the data quality and case mix criteria. For 2022 and 2023 the COVID-19 admissions were included in this dataset.
In addition to the above-mentioned criteria, hospitals are also excluded if they had not authorised CBS to supply their HSMR figures.
3.6 Computation of the model and the (H)SMR
3.6.1 SMR and HSMR
According to the first formula in section 1.1, the SMR of hospital h for diagnosis d is written as
with Odh the observed number of deaths with diagnosis d in hospital h, and Edh the expected number of deaths in a certain period. We can denote these respectively as
and
where Ddhi denotes the observed mortality for the ith admission of the combination (d,h), with scores 1 (death) and 0 (survival), and p̂dhi the mortality probability for this admission, as estimated by the logistic regression of “mortality diagnosis d” on the set of covariates mentioned in section 3.4. This gives
with Xdhi the scores of admission i of hospital h on the set of covariates, and the maximum likelihood estimates of 𝛽d, the corresponding regression coefficients, i.e. the so-called log-odds.
For the HSMR of hospital h, we have accordingly
It follows from the above formulae that:
Hence, an HSMR is a weighted mean of the SMRs, with the expected mortalities across diagnoses as the weights.
3.6.2 Modelling and model-diagnostics
We estimated a logistic regression model for each of the 158 CCS diagnosis groups, using the categorical covariates mentioned in section 3.4. Computations were performed using the glm routine of the statistical software R (R Core Team, 2015). Categories, including the reference category, are collapsed if the number of admissions is smaller than 50 or when there are no deaths in the category, to prevent standard errors of the regression coefficients becoming too large. This collapsing is performed starting with the smallest category, which is combined with the smallest nearby category, etc. For variables with only two categories collapsing results in dropping the covariate out of the model (except for comorbidities 17 (Severe liver disease) and 11 (Diabetes complications) which are first combined with comorbidity 9 (Liver disease), and comorbidity 10 (Diabetes), respectively; see section 3.4). Non-significant covariates are preserved in the model, unless the number of admissions is smaller than 50 (or if there are no deaths) for all but one category of a covariate. All regression coefficients are presented in a file published together with this report.
The following statistics are presented to evaluate the models:
- standard errors for all regression coefficients (published with the regression coefficients);
- statistical significance of the covariates with significance level α=.05, i.e. confidence level .95 (see “Statistical significance of covariates HSMR 2023 model” published together with this report);
- Wald statistics for the overall effect and the significance testing of categorical variables;
- C-statistics for the overall fit. The C-statistic is a measure for the predictive validity of, in our case, a logistic regression. Its maximum value of 1 indicates perfect discriminating power and 0.5 discriminating power not better than expected by chance, which will be the case if no appropriate covariates are found. We present the C-statistics as an evaluation criterion for the logistic regressions.
In addition to these diagnostic measures for the regressions, we present the average shift in HSMR by inclusion/deletion of the covariate in/from the model (table 4.4.1). This average absolute difference in HSMR is defined as
where
The Wald statistic is used to test whether the covariates have a significant impact on mortality, but it can also be used as a measure of association. A large value of a Wald statistic points to a strong impact of that covariate on mortality, adjusting for the impact of the other covariates. It is a kind of “explained chi-square”. As the number of categories may “benefit” covariates with many categories, it is necessary to also take into account the corresponding numbers of degrees of freedom (df), where the df is the number of categories minus one. As a result of collapsing the categories, the degrees of freedom can be smaller than the original number of categories minus one.
A high Wald statistic implies that the covariate’s categories discriminate in mortality rates. But if the frequency distribution of the covariate is equal for all hospitals, the covariate would not have any impact on the (H)SMRs. Therefore we also present the change in HSMRs resulting from deleting the covariate. Of course, a covariate that only has low Wald statistics has little impact on the (H)SMRs.
3.6.3 Confidence intervals and control limits
A confidence interval, i.e. an upper and lower confidence limit, is calculated for each SMR and HSMR. For the HSMR and most SMRs a confidence level of 95 percent is used, while for the SMRs of the 158 diagnosis groups a confidence level of 98 percent is used to reduce the number of undue statistically significant SMRs as a result of the large number of comparisons made when evaluating 158 diagnosis groups. A lower limit above 100 indicates a statistically significant high (H)SMR, and an upper limit below 100 a statistically significant low (H)SMR. In the calculation of these confidence intervals, a Poisson distribution is assumed for the numerator of the (H)SMR, while the denominator is assumed to have no variation. This is a good approximation, since the variance of the denominator is small. As a result of these assumptions, we were able to compute exact confidence limits.
3.6.4 Funnel plot HSMR (example)
<h3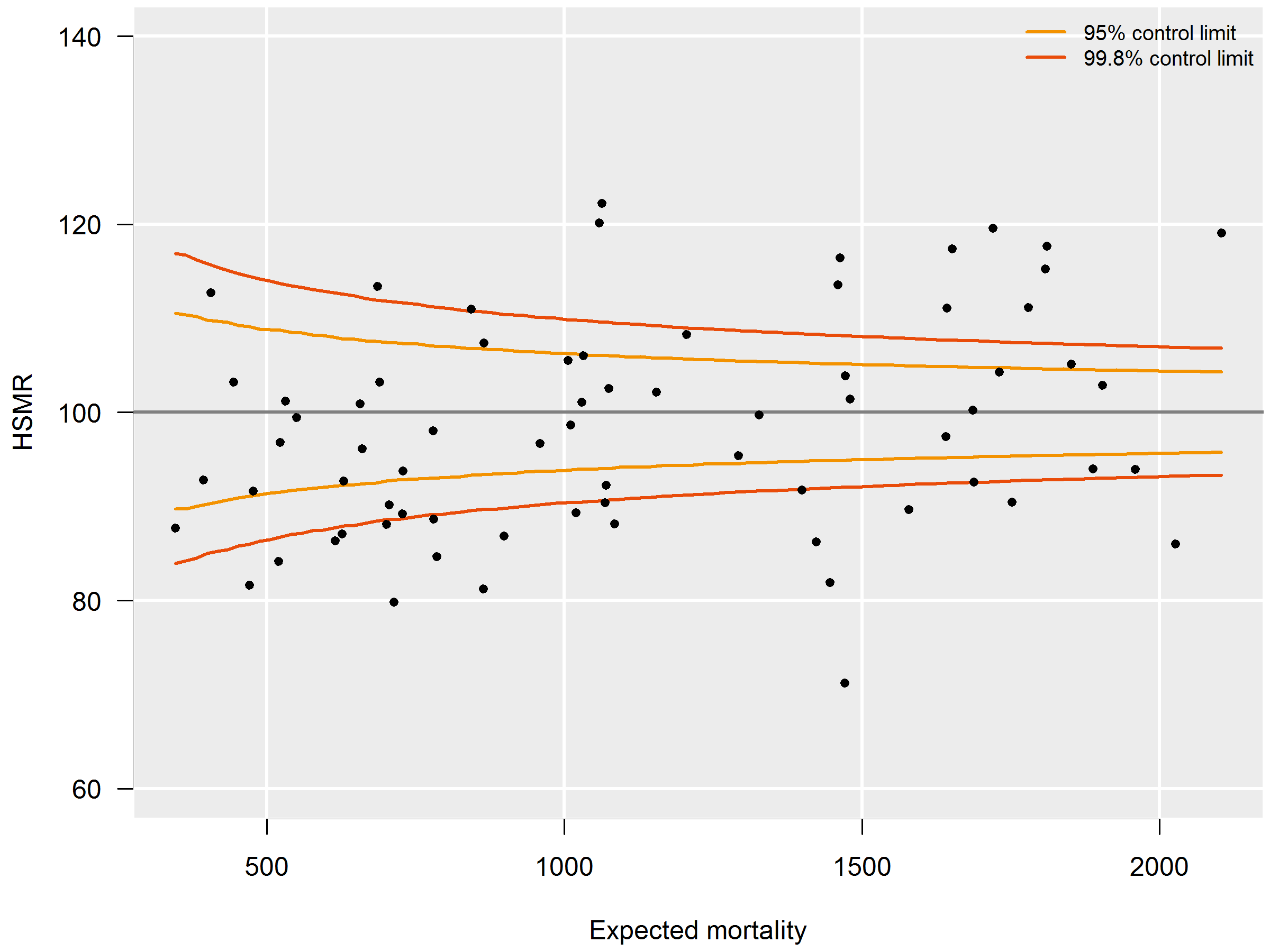
3.6.4 P-Values
2) For this criterion, all secondary diagnoses are considered, even if they do not belong to the 17 comorbidity groups used as covariates. If identical secondary diagnoses (identical ICD-10 codes) are registered within one admission, only one is counted. If a secondary diagnosis is identical to the main diagnosis of the admission, it is not counted as a secondary diagnosis.
4. Evaluation of the HSMR 2023 model
This chapter presents and evaluates the HSMR model results. Summary outcomes of the 158 logistic regressions are presented, with in-hospital mortality as the dependent variable and the variables mentioned in section 3.4 as explanatory variables. More detailed results are presented in the tables “Statistical significance of covariates HSMR 2023 model” and “Coefficients HSMR 2023”. These tables are published together with this report.
4.1 Target population and data set
All hospitals that register complete records of inpatient admissions and prolonged observations without overnight stay in the LBZ are included in the HSMR model. In 2020-2023 all general hospitals and university hospitals were included in the model, as well as three short-stay specialised hospitals (two cancer hospitals and an eye hospital). From 2022 onwards a fourth short-stay specialised (orthopaedic) hospital also participated in the LBZ and was included in the model as well. All of the hospitals had completely registered all admissions in the LBZ.
| 2020 | 2021 | 2022 | 2023 | total | |
|---|---|---|---|---|---|
| Excluded admissions not meeting the NZa criteria* | 123,889 | 131,521 | 143,399 | 148,014 | 546,823 |
| Excluded admissions of foreigners | 6,231 | 5,993 | 7,973 | 8,707 | 28,904 |
| Excluded admissions due to COVID-19** | 40,430 | 60,228 | 100,658 | ||
| Excluded admissions of healthy persons*** | 18,202 | 19,196 | 18,943 | 19,398 | 75,739 |
| Total number of admissions included in model | 1,395,545 | 1,407,749 | 1,481,648 | 1,489,868 | 5,774,810 |
| Number of inpatient admissions | 1,288,291 | 1,295,255 | 1,367,700 | 1,381,070 | 5,332,316 |
| Number of observations | 107,254 | 112,494 | 113,948 | 108,798 | 442,494 |
| Number of deaths included in model | 29,151 | 29,779 | 36,207 | 34,808 | 129,945 |
| Crude mortality (in admissions in model) | 2.1% | 2.1% | 2.4% | 2.3% | 2.3% |
| *Admissions that do not meet the billing criteria of the Dutch Healthcare Authority (NZa) for inpatient admissions, and for prolonged observations, unplanned, without overnight stay. The number of these admissions in the LBZ varies over the years, due to different registration instructions of DHD. **Admissions with COVID-19 as the main diagnosis (ICD-10 codes U07.1 (COVID-19, virus identified (lab confirmed)), U07.2 (COVID-19, virus not identified (clinically diagnosed)) and, from 2021 onwards, U10.9 (Multisystem inflammatory syndrome associated with COVID-19, unspecified)). *** Admissions of healthy persons are admissions of healthy newborns, healthy parents accompanying sick children, or other healthy boarders. | |||||
The total number of hospitals included in the HSMR model of 2020-2023 is 75 and includes 64 general hospitals, 7 university hospitals and 4 short stay specialised hospitals. These numbers are based on the number of hospital units in 2023, counting hospitals that merged in the period 2020-2023 as one unit for all years.
Table 4.1.1 lists some characteristics of the admissions included in the HSMR 2023 model per year. Admissions not meeting the criteria of the Dutch Healthcare Authority, admissions of foreigners and admissions of healthy persons were excluded. For the years 2020 and 2021, admissions with COVID-19 as the principal diagnosis were also excluded. The number of admissions included in 2023 (1,489,868) was comparable to the number of admissions in 2022 (1,481,648). The total number of admissions in the 2020-2023 model (5,774,810) however, is 2.2% lower than the total number of admissions in the previous model (2019-2022; 5,902,313). This decrease is due to the effect of the COVID-19 pandemic: the pre-pandemic year 2019, with substantially more admissions (1,617,371) than in the pandemic and post-pandemic years, was still included in the HSMR 2019-2022 model, but is excluded in the present 2020-2023 model.
Crude mortality of the admissions included in the HSMR model was increased in 2022 compared to mortality of previous years (partly due to the inclusion of COVID-19 admissions), but similar in 2023 (2.3%) compared to 2022 (2.4%).
4.2 Hospital exclusion
Hospitals were only provided with (H)SMR outcomes if the data fulfilled the criteria stated in paragraph 3.5. In order to qualify for a three-year report (2021-2023) hospitals had to fulfil these criteria for the three consecutive years.
Of the 75 hospitals included in the model, all had registered (valid) data over 2023. The four short stay specialised hospitals and one general hospital had not been asked to grant authorization for providing HSMR numbers because their case mix was very different from that of the other hospitals. In fact, all of these hospitals had participated in the LBZ but the data of these hospitals did not meet one or more of the previously stated criteria, such as a minimum number of 60 registered deaths or on average a minimum number of 1.5 comorbidities per admission. All of the other 70 hospitals that had granted authorization fulfilled the criteria and were provided with a HSMR figure for 2023. For these 70 hospitals the data of 2021 and 2022 was additionally investigated in order to determine if a three-year report could be provided. The data of all 70 hospitals met the criteria in all years considered and so all hospitals were also provided with three-year HSMR figures.
4.3 Impact of the covariates on mortality and HSMR
The table “Statistical significance of covariates HSMR 2023 model” published together with this report
shows which covariates have a statistically significant (95 percent confidence) impact on in-hospital mortality for
each of the 158 diagnosis groups: “1” indicates (statistical) significance, and “0”
non-significance, while a dash (-) means that the covariate has been dropped as the number of admissions is smaller
than 50 (or as there are no deaths) for all but one category of a covariate; see section 3.6.2.
The last row of the table “Statistical significance of covariates HSMR 2023 model” published together
with this report gives the numbers of significant results across the diagnosis groups for each covariate. These
values are presented again in table 4.3.1, as a summary, but ordered by the number of times a covariate is
significant. Age, urgency of the admission, and severity of the main diagnosis are significant for a large majority
of the diagnosis groups. This is also true for several of the comorbidity groups, especially for group 2 (Congestive
heart failure and cardiomyopathy). Comorbidity 15 (HIV) is only rarely registered as a comorbidity; most diagnosis
groups had fewer than 50 admissions with HIV comorbidity. In only one of the models comorbidity 15 is statistically
significant. The number of times month of admission is significant varies over the years (CBS, 2017, 2018, 2019,
2020, 2021, 2022): it increased from 27 in 2017 to 43 in 2018 and decreased steadily since 2019 to 28 in 2022. In
2023 it increases slightly to 32. The number of times year of discharge is significant was 22 in the HSMR models of
2019, 2020 and 2021, increased substantially to 32 in 2022 (CBS 2020, 2021, 2022, 2023), and drops again to 26 in
2023. Compared to the HSMR 2022 model, other large changes were observed for the covariate comorbidity 3 (Peripheral
vascular disease): it was significant in 95 models in 2021, increased to 103 in 2022, and decreases again to 91
models in 2023. The changes are smaller for the other covariates. The total number of significant covariates
decreased from 1,613 in 2022 to 1,586 in 2023.
| var | No. of significant results |
|---|---|
| Age | 141 |
| Urgency | 127 |
| Comorbidity 2 | 126 |
| Severity main diagnosis | 114 |
| Comorbidity 13 | 106 |
| Comorbidity 16 | 104 |
| Comorbidity 9 | 94 |
| Source of admission | 94 |
| Comorbidity 3 | 91 |
| Comorbidity 6 | 82 |
| Comorbidity 14 | 64 |
| Comorbidity 4 | 61 |
| Comorbidity 5 | 57 |
| Comorbidity 17 | 45 |
| Comorbidity 1 | 41 |
| Sex | 39 |
| Month of admission | 32 |
| Comorbidity 10 | 29 |
| Comorbidity 12 | 27 |
| Comorbidity 7 | 27 |
| Comorbidity 11 | 26 |
| Year of discharge | 26 |
| SES | 21 |
| Comorbidity 8 | 11 |
| Comorbidity 15 | 1 |
| Comorbidity groups: 1 Myocardial infarction, 2 Congestive heart failure and cardiomyopathy, 3 Peripheral vascular disease, 4 Cerebrovascular disease , 5 Dementia, 6 Pulmonary disease, 7 Connective tissue disorder, 8 Peptic ulcer, 9 Liver disease, 10 Diabetes, 11 Diabetes complications, 12 Hemiplegia or paraplegia, 13 Renal disease, 14 Cancer, 15 HIV, 16 Metastatic cancer, 17 Severe liver disease. | |
The significance only partially reflects the effect of the covariates on mortality. This is better measured using the Wald statistic. Table 4.3.2 presents the total of all Wald statistics summed over the diagnosis groups with the respective sum of the degrees of freedom, for each of the covariates ordered by value. It shows that severity of the main diagnosis has the highest explanatory power. Age and urgency of admission are also important variables. Of the comorbidities in the model, comorbidity groups 2, 16, and 13 are the groups with the most impact on mortality. Compared to the outcome of the 2022 model (CBS, 2023), the order of the covariates with regard to explanatory power is almost identical. Note that the values of the Wald statistics themselves cannot be compared directly between years as these values depend on the number of admissions used in the models.
| Covariate | Sum of Wald statistics | Sum of df |
|---|---|---|
| Severity main diagnosis | 39,017 | 408 |
| Age | 30,489 | 2,000 |
| Urgency | 16,082 | 156 |
| Comorbidity 2 | 9,285 | 147 |
| Comorbidity 16 | 4,082 | 139 |
| Comorbidity 13 | 3,485 | 151 |
| Source admission | 2,929 | 281 |
| Comorbidity 3 | 2,415 | 147 |
| Comorbidity 6 | 1,979 | 152 |
| Month of admission | 1,653 | 788 |
| Comorbidity 9 | 1,601 | 123 |
| Comorbidity 17 | 1,496 | 66 |
| Comorbidity 4 | 1,249 | 122 |
| Comorbidity 14 | 1,225 | 144 |
| Comorbidity 5 | 1,221 | 119 |
| SES | 1,013 | 706 |
| Year of discharge | 913 | 468 |
| Sex | 837 | 150 |
| Comorbidity 12 | 791 | 99 |
| Comorbidity 1 | 641 | 149 |
| Comorbidity 10 | 395 | 152 |
| Comorbidity 7 | 308 | 129 |
| Comorbidity 11 | 282 | 114 |
| Comorbidity 8 | 137 | 32 |
| Comorbidity 15 | 14 | 11 |
| Comorbidity groups: 1 Myocardial infarction, 2 Congestive heart failure and cardiomyopathy, 3 Peripheral vascular disease, 4 Cerebrovascular disease , 5 Dementia, 6 Pulmonary disease, 7 Connective tissue disorder, 8 Peptic ulcer, 9 Liver disease, 10 Diabetes, 11 Diabetes complications, 12 Hemiplegia or paraplegia, 13 Renal disease, 14 Cancer, 15 HIV, 16 Metastatic cancer, 17 Severe liver disease. | ||
The explanatory power of year of discharge increases since the HSMR 2021 model, with the largest increase in 2022 (13%) and a further small increase of 3.2% in this year’s HSMR 2023 model. This implies that the
differences in mortality between the years in the model (corrected for differences in patient characteristics) has
slightly increased. The impact of comorbidity 1 (myocardial infarction) has stabilized after having decreased for
seven years.
In addition, the impact of comorbidity 14 (cancer) has decreased by 33% since the 2016 model. A decreased impact of
a comorbidity could reflect a decreased effect of the comorbidity (e.g. the likelihood of dying in hospital when
having this condition as comorbidity has decreased), and/or a decreased number of patients with this comorbidity
resulting in less accurate estimates of the effect of this comorbidity (which also decreases the Wald statistic).
The opposite applies in the case of an increased impact of a variable.
The impact of month of admission has increased considerably in the 2022 (12%) and 2023 models (8%). The increase in
2022 is probably caused by the inclusion of COVID-19 in the 2022 model for which month of admission is an important
predictor. In 2023 the increase of the impact of month of admission is mostly caused by diagnoses other than
COVID-19, such as pneumonia. As was mentioned in section 3.6.2, when the hospitals differ little on a covariate, the
effect of this covariate on the HSMR can still be small even if this covariate is a strong predictor for mortality.
Table 4.3.3 shows the impact of each covariate on the HSMR, as measured by the formula in paragraph 3.6.2, for the
hospitals for which HSMRs are calculated. The comorbidities, which are considered here as one group (17
comorbidities together), have the largest effect on the HSMR. This is caused by differences in case mixes between
hospitals, but possibly also by differences in coding practices (see Van der Laan, 2013). The effect of
comorbidities has increased somewhat (from 4.25 to 5.05) compared to the 2022 HSMR model. Deleting sex as a
covariate hardly has an impact on the HSMRs, whereas SES has a reasonable impact on the HSMR. This is probably
because hospitals differ more in terms of SES categories of the postal areas in their vicinity than in terms of the
sex distribution of their patients. In general, the magnitudes of the effect on the HSMR of the covariates shown in
table 4.3.3 are about the same as in the previous model.
| Covariate | Average shift in HSMR |
|---|---|
| Comorbidity* | 5.05 |
| Age | 3.68 |
| Severity main diagnosis | 2.25 |
| Urgency | 1.92 |
| Source of admission | 0.99 |
| SES | 0.96 |
| Month of admission | 0.13 |
| Sex | 0.12 |
| *The comorbidities were deleted as one group and not separately. | |
4.4 Model evaluation for the 158 regression analyses
Table 4.4.1 presents numbers of admissions and deaths, and C-statistics for the 158 diagnosis groups. The
C-statistic is explained in section 3.6.2. Overall the C-statistics have changed little compared to the previous
model. Only three C-statistics show a moderate increase: an increase from 0.94 to 0.99 for “Cancer of testis and other male genital organs” (24), an increase from
0.88 to 0.92 for “Cystic fibrosis” (43) and an increase from 0.86 to 0.91 for “Complications
of pregnancy, childbirth, and the puerperium; liveborn” (118). All other changes are smaller than 0.04, with
most below 0.02. For 67 diagnosis groups the C-statistic did not change compared to last year.
Only two of the 158 diagnosis groups have a C-statistic below 0.70: “Congestive heart failure,
nonhypertensive” (70), and “Aspiration pneumonitis; food/vomitus” (84). For the diagnosis
groups with a C-statistic below 0.70, the model’s ability to explain patient mortality is less than
‘good’. This increases the risk that the model does not completely correct for population
differences between the hospitals. For the highest scoring diagnosis groups (0.90 and above) the covariates
strongly reduce the uncertainty in predicting patient mortality. In 2023, 65 diagnosis groups had a C-statistic
above or equal to 0.90, compared to 64 diagnosis groups in 2022.
As mentioned in chapter 2 and section 3.4, it was decided not to change the model for COVID-19 compared to last
year - except for adding year of discharge as we now have two years of data in the model (2022 and 2023). Only
in case the model quality would deteriorate significantly (resulting in a C-statistic <0.7), we would
consider changing the model. As the C-statistic has decreased only slightly from 0.75 to 0.74 (see table 4.4.1),
we did not change the COVID-19 model. However, as we only use additive models (without interactions) in
calculating the HSMR, the present two year’s COVID-19 model with month of admission and year of discharge
does not capture all of the differences in the COVID-19 waves between 2022 and 2023 (the months at which they
occurred differ and the COVID-19 variants differ; see section 3.4). As the C-statistic of the present two
year’s model is almost the same as in the previous one year model, this had little effect on the model
quality.
| Diag. group no. | Description of diagnosis group | Number of admis- sions | Number of deaths | C-statistic |
|---|---|---|---|---|
| 1 | Tuberculosis | 1,469 | 48 | 0.87 |
| 2 | Septicemia (except in labor) | 11,348 | 3,312 | 0.72 |
| 3 | Bacterial infection, unspecified site | 10,059 | 664 | 0.80 |
| 4 | Mycoses | 2,674 | 329 | 0.78 |
| 5 | HIV infection | 725 | 23 | 0.83 |
| 6 | Hepatitis, viral and other infections | 23,166 | 299 | 0.93 |
| 7 | Cancer of head and neck | 14,475 | 239 | 0.90 |
| 8 | Cancer of esophagus | 9,516 | 584 | 0.78 |
| 9 | Cancer of stomach | 10,082 | 439 | 0.82 |
| 10 | Cancer of colon | 41,039 | 1,098 | 0.83 |
| 11 | Cancer of rectum and anus | 16,514 | 383 | 0.86 |
| 12 | Cancer of liver and intrahepatic bile duct | 7,354 | 466 | 0.82 |
| 13 | Cancer of pancreas | 16,006 | 899 | 0.81 |
| 14 | Cancer of other GI organs, peritoneum | 8,565 | 375 | 0.80 |
| 15 | Cancer of bronchus, lung | 44,395 | 4,074 | 0.80 |
| 16 | Cancer, other respiratory and intrathoracic | 2,061 | 140 | 0.82 |
| 17 | Cancer of bone and connective tissue | 8,034 | 94 | 0.92 |
| 18 | Melanomas of skin and other non-epithelial cancer of skin | 5,724 | 111 | 0.94 |
| 19 | Cancer of breast | 37,178 | 371 | 0.97 |
| 20 | Cancer of uterus | 9,049 | 126 | 0.94 |
| 21 | Cancer of cervix and other female genital organs | 10,015 | 87 | 0.93 |
| 22 | Cancer of ovary | 7,717 | 239 | 0.85 |
| 23 | Cancer of prostate | 24,785 | 326 | 0.94 |
| 24 | Cancer of testis and other male genital organs | 6,375 | 5 | 0.99 |
| 25 | Cancer of bladder | 53,078 | 431 | 0.93 |
| 26 | Cancer of kidney, renal pelvis and other urinary organs | 15,520 | 288 | 0.89 |
| 27 | Cancer of brain and nervous system | 11,590 | 234 | 0.78 |
| 28 | Cancer of thyroid | 6,060 | 51 | 0.98 |
| 29 | Hodgkin`s disease | 1,701 | 42 | 0.92 |
| 30 | Non-Hodgkin`s lymphoma | 22,872 | 961 | 0.83 |
| 31 | Leukemias | 21,318 | 1,201 | 0.80 |
| 32 | Multiple myeloma | 9,963 | 438 | 0.80 |
| 33 | Cancer, other and unspec. primary, maintenance chemotherapy and radioth. | 4,413 | 110 | 0.90 |
| 34 | Secondary malignancies | 77,034 | 4,179 | 0.77 |
| 35 | Malignant neoplasm without specification of site | 2,151 | 345 | 0.81 |
| 36 | Neoplasms of unspecified nature or uncertain behavior | 10,936 | 214 | 0.88 |
| 37 | Other and unspecified benign neoplasm | 61,439 | 117 | 0.85 |
| 38 | Thyroid and other endocrine disorders | 22,886 | 234 | 0.90 |
| 39 | Diabetes mellitus without complication | 12,486 | 137 | 0.87 |
| 40 | Diabetes mellitus with complications | 23,253 | 498 | 0.85 |
| 41 | Nutritional deficiencies and other nutritional, endocrine, and metabolic disorders | 53,923 | 492 | 0.94 |
| 42 | Fluid and electrolyte disorders | 31,935 | 923 | 0.84 |
| 43 | Cystic fibrosis | 1,460 | 7 | 0.92 |
| 44 | Immunity and coagulation disorders, hemorrhagic disorders | 10,393 | 182 | 0.88 |
| 45 | Deficiency and other anemia | 47,701 | 492 | 0.79 |
| 46 | Diseases of white blood cells | 8,986 | 256 | 0.77 |
| 47 | Mental, affective, anxiety, somatoform, dissociative, and personality disorders | 19,611 | 58 | 0.90 |
| 48 | Senility and organic mental disorders | 10,183 | 568 | 0.71 |
| 49 | Schizophrenia, mental retardation, preadult disorders and other mental cond. | 6,040 | 21 | 0.94 |
| 50 | Other psychoses | 2,526 | 21 | 0.88 |
| 51 | Meningitis, encephalitis, and other central nervous system infections | 9,537 | 567 | 0.88 |
| 52 | Parkinson`s disease | 4,915 | 96 | 0.84 |
| 53 | Multiple sclerosis and other degenerative nervous system conditions | 10,761 | 282 | 0.90 |
| 54 | Paralysis and late effects of cerebrovascular disease | 3,404 | 56 | 0.88 |
| 55 | Epilepsy and convulsions | 41,641 | 601 | 0.88 |
| 56 | Coma, stupor, and brain damage | 1,956 | 189 | 0.91 |
| 57 | Headache and other disorders of the sense organs | 55,486 | 43 | 0.92 |
| 58 | Other nervous system disorders | 43,877 | 395 | 0.93 |
| 59 | Heart valve disorders | 35,800 | 813 | 0.78 |
| 60 | Peri-, endo-, myocarditis, and cardiomyopathy | 21,043 | 630 | 0.87 |
| 61 | Essential hypertension, hypertension with compl., and secondary hypertension | 12,163 | 120 | 0.95 |
| 62 | Acute myocardial infarction | 135,542 | 3,404 | 0.85 |
| 63 | Coronary atherosclerosis and other heart disease | 94,141 | 720 | 0.84 |
| 64 | Nonspecific chest pain | 132,899 | 38 | 0.91 |
| 65 | Pulmonary heart disease | 30,495 | 1,056 | 0.79 |
| 66 | Other and ill-defined heart disease | 1,232 | 100 | 0.87 |
| 67 | Conduction disorders (heart disease) | 24,861 | 399 | 0.87 |
| 68 | Cardiac dysrhythmias | 165,244 | 741 | 0.90 |
| 69 | Cardiac arrest and ventricular fibrillation | 15,705 | 5,727 | 0.75 |
| 70 | Congestive heart failure, nonhypertensive | 127,317 | 10,160 | 0.66 |
| 71 | Acute cerebrovascular disease | 156,017 | 13,090 | 0.80 |
| 72 | Transient cerebral ischemia, and other cerebrovascular disease | 41,809 | 302 | 0.90 |
| 73 | Peripheral and visceral atherosclerosis | 46,722 | 1,970 | 0.90 |
| 74 | Aortic and other artery aneurysms | 26,933 | 2,448 | 0.89 |
| 75 | Aortic and arterial embolism or thrombosis | 10,350 | 425 | 0.85 |
| 76 | Other circulatory disease | 29,698 | 580 | 0.86 |
| 77 | Phlebitis, varicose veins, and hemorrhoids | 9,970 | 134 | 0.88 |
| 78 | Pneumonia | 106,470 | 9,005 | 0.75 |
| 79 | Influenza | 17,964 | 790 | 0.80 |
| 80 | Tonsillitis and upper respiratory infections | 43,513 | 68 | 0.92 |
| 81 | Acute bronchitis | 28,885 | 89 | 0.94 |
| 82 | Chronic obstructive pulmonary disease and bronchiectasis | 97,218 | 6,261 | 0.70 |
| 83 | Asthma | 22,981 | 92 | 0.91 |
| 84 | Aspiration pneumonitis, food/vomitus | 7,936 | 1,671 | 0.64 |
| 85 | Pleurisy, pneumothorax, pulmonary collapse | 21,468 | 620 | 0.82 |
| 86 | Respiratory failure, insufficiency, arrest | 4,983 | 1,533 | 0.73 |
| 87 | Lung disease due to external agents | 1,738 | 165 | 0.76 |
| 88 | Other lower respiratory disease | 24,590 | 1,017 | 0.88 |
| 89 | Other upper respiratory disease | 43,770 | 292 | 0.89 |
| 90 | Intestinal infection | 43,128 | 518 | 0.88 |
| 91 | Disorders of mouth, teeth, and jaw | 19,880 | 53 | 0.96 |
| 92 | Esophageal disorders | 11,550 | 133 | 0.89 |
| 93 | Gastroduodenal ulcer | 5,124 | 225 | 0.91 |
| 94 | Gastritis, duodenitis, and other disorders of stomach and duodenum | 7,230 | 90 | 0.87 |
| 95 | Appendicitis and other appendiceal conditions | 69,811 | 79 | 0.96 |
| 96 | Peritonitis and intestinal abscess | 5,103 | 376 | 0.81 |
| 97 | Abdominal hernia | 42,280 | 505 | 0.90 |
| 98 | Regional enteritis and ulcerative colitis | 16,929 | 62 | 0.95 |
| 99 | Intestinal obstruction without hernia | 32,890 | 1,556 | 0.82 |
| 100 | Diverticulosis and diverticulitis | 35,201 | 531 | 0.91 |
| 101 | Anal and rectal conditions | 21,025 | 55 | 0.94 |
| 102 | Biliary tract disease | 106,813 | 1,043 | 0.89 |
| 103 | Liver disease, alcohol-related | 7,404 | 934 | 0.72 |
| 104 | Other liver diseases | 18,231 | 1,109 | 0.81 |
| 105 | Pancreatic disorders (not diabetes) | 36,807 | 888 | 0.83 |
| 106 | Gastrointestinal hemorrhage | 35,841 | 1,047 | 0.80 |
| 107 | Noninfectious gastroenteritis | 10,431 | 234 | 0.80 |
| 108 | Other gastrointestinal disorders | 32,423 | 783 | 0.94 |
| 109 | Nephritis, nephrosis, renal sclerosis | 14,317 | 117 | 0.90 |
| 110 | Acute and unspecified renal failure | 14,545 | 1,015 | 0.77 |
| 111 | Chronic kidney disease | 12,972 | 431 | 0.87 |
| 112 | Urinary tract infections | 95,678 | 2,853 | 0.77 |
| 113 | Calculus and other diseases of urinary tract | 76,682 | 186 | 0.92 |
| 114 | Genitourinary symptoms and ill-defined conditions | 25,702 | 148 | 0.87 |
| 115 | Hyperplasia of prostate and other male genital disorders | 41,866 | 59 | 0.94 |
| 116 | Non-neoplastic breast conditions | 11,115 | 3 | 0.99 |
| 117 | Prolapse and other female genital disorders | 58,892 | 39 | 0.99 |
| 118 | Complications of pregnancy, childbirth, and the puerperium, liveborn | 541,603 | 15 | 0.91 |
| 119 | Skin and subcutaneous tissue infections | 54,104 | 847 | 0.89 |
| 120 | Other skin disorders, chronic ulcer of skin | 16,191 | 224 | 0.92 |
| 121 | Infective arthritis and osteomyelitis | 13,930 | 327 | 0.90 |
| 122 | Osteoarthritis, rheumatoid arthritis, and other musculoskeletal deformities | 228,065 | 173 | 0.94 |
| 123 | Other non-traumatic joint disorders | 9,770 | 32 | 0.93 |
| 124 | Spondylosis, back problems, and osteoporosis | 79,768 | 190 | 0.96 |
| 125 | Pathological fracture | 4,798 | 80 | 0.83 |
| 126 | Other connective tissue disease | 28,254 | 307 | 0.96 |
| 127 | Cardiac and circulatory congenital anomalies | 8,839 | 153 | 0.89 |
| 128 | Noncardiac congenital anomalies | 25,422 | 167 | 0.94 |
| 129 | Short gestation, low birth weight, and fetal growth retardation | 77,344 | 493 | 0.86 |
| 130 | Intrauterine hypoxia, perinatal asphyxia, and jaundice | 61,431 | 226 | 0.95 |
| 131 | Other perinatal conditions | 228,985 | 227 | 0.95 |
| 132 | Joint disorders and dislocations, trauma-related, sprains and strains | 18,146 | 32 | 0.97 |
| 133 | Fracture of neck of femur (hip) | 89,111 | 2,811 | 0.80 |
| 134 | Skull and face fractures, spinal cord injury | 11,095 | 224 | 0.90 |
| 135 | Fracture of upper limb | 40,440 | 137 | 0.95 |
| 136 | Fracture of lower limb | 49,375 | 306 | 0.94 |
| 137 | Other fractures | 43,975 | 1,088 | 0.85 |
| 138 | Intracranial injury | 39,809 | 2,851 | 0.76 |
| 139 | Crushing injury or internal injury | 20,146 | 422 | 0.91 |
| 140 | Open wounds of head, neck, and trunk | 5,471 | 57 | 0.87 |
| 141 | Open wounds of extremities | 4,948 | 36 | 0.93 |
| 142 | Complication of device, implant or graft | 96,912 | 1,370 | 0.87 |
| 143 | Complications of surgical procedures or medical care | 98,727 | 912 | 0.85 |
| 144 | Superficial injury, contusion | 56,502 | 489 | 0.92 |
| 145 | Burns | 3,657 | 80 | 0.92 |
| 146 | Poisoning by psychotropic agents, drugs, or other medications | 35,827 | 355 | 0.86 |
| 147 | Other injuries and conditions due to external causes | 13,653 | 727 | 0.89 |
| 148 | Syncope | 40,937 | 129 | 0.85 |
| 149 | Fever of other and unknown origin | 17,374 | 86 | 0.82 |
| 150 | Lymphadenitis and gangrene | 3,735 | 20 | 0.96 |
| 151 | Shock | 1,315 | 507 | 0.74 |
| 152 | Nausea and vomiting | 10,956 | 58 | 0.87 |
| 153 | Abdominal pain | 34,503 | 95 | 0.94 |
| 154 | Malaise and fatigue | 8,482 | 150 | 0.79 |
| 155 | Allergic reactions | 10,270 | 34 | 0.95 |
| 156 | Rehabilitation and other aftercare, medical examination/evaluation/screening | 69,654 | 227 | 0.84 |
| 157 | Residual codes, unclassified | 28,159 | 165 | 0.95 |
| 158 | COVID-19 | 44,440 | 4,124 | 0.74 |
4.5 Regression coefficients
The file “coefficients HSMR 2023.xls” contains the estimated regression coefficients (columns
“Estimate”), also called “log-odds”, for each of the 158 logistic regressions, as
well as their standard errors (columns “Std. Err.”).
The estimated regression coefficients are the elements of the estimate of vector 𝛽d in the formula for p̂dhi (see section 3.6.1), for each diagnosis d.
Notice that a β-coefficient has to be interpreted as the difference in log-odds between the category in question and
the reference category (first category of the same covariate). For the sake of clarity, the reference
categories are given in the first row of the corresponding covariates and these have by definition a zero
coefficient for each regression.
In many cases categories are collapsed (see section 3.6.2). This results in equal coefficients for the
collapsed categories. If all categories were collapsed into one category for a certain variable and for a
certain diagnosis group (i.e. if there was only one category with ≥50 admissions and ≥1 death), the
variable was dropped from the model and all associated coefficients were set to zero. Therefore, the
coefficients in the file “coefficients HSMR 2023” can be used directly to calculate
mortality probabilities, with the exception of two of the Charlson comorbidities (Comorbidity 17 and
Comorbidity 11). If Charlson comorbidity 17 (Severe liver disease) contains <50 admissions or no
mortality, it is collapsed with Charlson comorbidity 9 (Liver disease). In this case the coefficient of
Comorbidity 17 is set to zero. When a patient has both comorbidities, it counts as only one comorbidity.
Therefore, when the coefficient of Comorbidity 17 is zero in the coefficients file, one should first recode
all Charlson 17 comorbidities to Comorbidity 9 and use the coefficient of Comorbidity 9. The same holds for
Charlson 11 (Diabetes complications) when it is collapsed with Charlson 10 (Diabetes).
5. Conclusions
No changes have been implemented to the HSMR 2023 model compared to the model of previous year. The COVID-19 model was also kept the same as previous year. Only the covariate “Year of discharge” was added to the COVID-19 model as there are now two years in the model (2022 and 2023), compared to one year (2022) in the previous model. As the predictive power of the model remained the same, further investigation into possible improvements was not performed.
To be able to distinguish different COVID-19 waves the additional category “before Year of discharge” was introduced to the covariate “Month of admission” in the COVID-19 model last year. An admission in e.g. December 2022 (and discharge in 2022) was thus distinguished from an admission in December 2021 and discharge in 2022, because the latter admission was given the category “before Year of discharge” for Month of admission. This also holds true now that there are two years in the model, with Year of discharge added as a covariate. With this covariate, it is possible to distinguish between an admission in December 2023 with a discharge in 2023 and an admission in December 2022 with a discharge in 2023. For the latter, Month of admission will be equal to “before Year of discharge” instead of “December”. However, since interactions are not included in the model, it is not possible to properly distinguish different COVID-19 wave patterns over the years. There is, for example, only one coefficient for “March” that is used both for admissions from 2022 and from 2023. Another disadvantage is that the “before Year of discharge” admissions on average have longer lengths of stay than the other admissions, as the month of discharge is later than the month of admission. In principle we do not want to correct for length of stay in the HSMR model, only for characteristics at the moment of admission. Although the effects of these disadvantages on the SMR will probably be small, it may be good to check whether the present COVID-19 model is still the most adequate for the HSMR 2024, with multiple years in the model.
Sections 4.4 and 4.5 evaluate the quality of the present HSMR model. The C-statistics have changed little compared to the previous model. The order of the covariates with regard to explanatory power is mostly the same, although some minor changes have occurred in the relative importance of some of the variables. The importance of month of admission has increased a bit further and the importance of year of discharge has dropped again after an increase 2022. Overall, the model and the quality of the model have changed little compared to previous year.
6. References
Arts, K., R. van Gaalen, J. van der Laan, F. Linder, J. Mol, J. van Rooijen and C. Siermann (2022). Berekenwijze Sociaal Economische Status scores, Statistics Netherlands, The Hague/Heerlen.
Bottle, A., B. Jarman and P. Aylin (2011). Hospital standardized mortality ratios: sensitivity analyses on the impact of coding. Health Serv Res 46(6 Pt 1):1741–61.
Campbell, M.J., R.M. Jacques, J. Fotheringham, T. Pearson, R. Maheswaran and J. Nicholl (2011). An evaluation of the Summary Hospital Mortality Index, final report. School of Health and Related Research, The University of Sheffield.
CBS (2011, 2012, 2013,… etc.). HSMR 2010 [2011, 2012, …etc.], Methodological report. Statistics Netherlands, The Hague/Heerlen.
Cecil, E., A. Bottle, A. Esmail, C. Vincent and P. Aylin (2020). What is the relationship between mortality alerts and other indicators of quality of care? A national cross-sectional study. Journal of Health Services Research & Policy 25(1): 13-21.
Chong, C.A.K.Y., G.C. Nguyen and M.E. Wilcox (2012). Trends in Canadian hospital standardised mortality ratios and palliative care coding 2004-2010: a retrospective database analyses.. BMJ Open 2012;2:e001729. doi:10.1136/bmjopen-2012-001729.
Goeman, J.J. and A. Solari (2011). Multiple Testing for Exploratory Research. Statist. Sci. 26 (4), November 2011. https://doi.org/10.1214/11-STS356, 584-597.
Haas, E.J., F.J. Angulo, J.M. McLaughlin, E. Anis, S.R. Singer, F. Khan, ... & S. Alroy-Preis (2021). Impact and effectiveness of mRNA BNT162b2 vaccine against SARS-CoV-2 infections and COVID-19 cases, hospitalisations, and deaths following a nationwide vaccination campaign in Israel: an observational study using national surveillance data. The Lancet, 397(10287), 1819-1829.
Heijink, R., X. Koolman, D. Pieter, A. van der Veen, B. Jarman and G. Westert (2008). Measuring and explaining mortality in Dutch hospitals; The Hospital Standardized Mortality Rate between 2003 and 2005. BMC Health Services Research 8:73.
HSCIC (2016). Indicator Specification: Summary Hospital-level Mortality Indicator. Version 1.22, 24 February 2016. Health & Social Care Information Centre.
Jarman, B., D. Pieter, A.A. van der Veen, R.B. Kool, P. Aylin, A. Bottle and G.P. Westert (2010). The hospital standardised mortality ratio: a powerful tool for Dutch hospitals to assess their quality of care? Qual Saf Healthcare 19, 9-13.
Jarman, B., S. Gault, B. Alves, A. Hider, S. Dolan, A. Cook, B. Hurwitz and L.I. Iezzoni (1999). Explaining differences in English hospital death rates using routinely collected data, BMJ 318, 1515-1519.
Lamarche-Vadel, A., M. Ngantcha, M.-A. Le Pogamm, C. Grenier, L. Meyer and G. Rey (2015). Hospital comparisons based on mortality: revisiting the choice of postadmission timeframe and evaluating the contribution of cause-of-death data, France, 2009. Medical Care 53, 736-742.
Lilford, R. and P. Pronovost (2010). Using hospital mortality rates to judge hospital performance: a bad idea that just won’t go away. BMJ 340:c2016.
Mitchell, T.M. (2016). “Estimating Probabilities” additional chapter for the book Mitchell, T.M. (1997). Machine Learning. McGraw-Hill, New York.
NHS - The Health and Social Care Information Centre (2013). The use of palliative care coding in the Summary Hospital-level Mortality Indicator.
Ploemacher, J, A.Z. Israëls, D.J. van der Laan and A. de Bruin (2013). Gestandaardiseerde ziekenhuissterfte daalt in de tijd. Ned Tijdschr Geneeskd. 157 (22), 1034-1039.
Pouw, M.E., L.M. Peelen, K.G.M. Moons, C.J. Kalkman and H.F. Lingsma (2013). Including post-discharge mortality in the calculation of hospital standardised mortality ratios: a retrospective analysis of hospital episode statistics. BMJ 347:f5913.
Prismant (2008). De toepasbaarheid van de HSMR in het toezicht van de inspectie voor de gezondheidszorg. Prismant, Utrecht.
Quan H, V. Sundararajan, P. Halfon, A. Fong A, B. Burnand, J.C. Luthi, L.D. Saunders, C.A. Beck, T. E. Feasby, W.A. Ghali (2005). Coding algorithms for defining comorbidities in ICD-9-CM and ICD-10 administrative data. Medical Care 43, 1130-1139.
R Core Team (2015). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria.
RIVM and CBS (2022). Sterfte en oversterfte in 2020 en 2021: Onderzoek door het CBS en het RIVM, in het kader van het ZonMw onderzoeksprogramma Oversterfte. National Institute for Public Health and the Environment (RIVM), Bilthoven, and Statistics Netherlands (CBS), The Hague/Heerlen.
Van den Bosch, W.F., J. Silberbusch, K.J. Roozendaal and C. Wagner (2010). Variatie in codering patiëntengegevens beïnvloedt gestandaardiseerd ziekenhuissterftecijfer. Ned Tijdschr Geneeskd. 154 (2), 1-9.
Van den Bosch, W.F., P. Spreeuwenberg and C. Wagner (2011). Gestandaardiseerd ziekenhuissterftecijfer (HSMR): correctie voor ernst hoofddiagnose kan beter. Ned Tijdschr Geneeskd. 155:A3299, 66-75.
Van der Laan, D.J. (2013). Quality of the Dutch Medical Registration (LMR) for the calculation of the Hospital Standardised Mortality Ratio. Statistics Netherlands, The Hague/Heerlen.
Van der Laan, D.J., A. de Bruin, J. van den Akker-Ploemacher and Frank Pijpers (2015). Post-discharge mortality in the Hospital Standardized Mortality Ratio. Discussion Papers, Statistics Netherlands, The Hague/Heerlen.
Van der Laan, D.J. and A. de Bruin (2016). Uitbreiding hoofddiagnosegroepen in de HSMR. Discussion Paper, Statistics Netherlands, The Hague/Heerlen.
Van Erven, J.A., L.S. van Galen, A.A. Hettinga-Roest, E.P.J. Claessens, J.C. Roos, M.H.H. Kramer and P.W.B Nanayakkara (2018). Hospital standardised mortality ratio: A reliable indicator of quality of care?. Neth J Med 76(2): 72-77.
Van Gestel, Y.R.B.M., V.E.P.P. Lemmens, H.F. Lingsma, I.H.J.T. de Hingh, H.J.T Rutten and J.W.W Coebergh (2012). The hospital standardized mortality ratio fallacy; a narrative review. Medical Care 50 (8), 662-667.
Appendix
The Excel file ‘Statistical significance of covariates HSMR 2023 model’ presents the statistical significance (95% confidence) of the covariates for the 158 logistic regressions.
Excel file ‘Classification of variables HSMR 2023’ contains the classifications used for the diagnosis groups, severity of main diagnosis, socio-economic status and source of admission.
Excel file ‘Coefficients HSMR 2023’ contains the coefficients and standard errors of the HSMR model by diagnosis group.