3. Resultaten herijking model
In dit hoofdstuk presenteren we de resultaten van de verschillende modellen. Zoals beschreven in het vorige hoofdstuk hebben we een stapsgewijze aanpak gehanteerd om te komen tot een geactualiseerd model voor de po-indicator. We beginnen met een basismodel dat is geschat met behulp van de grotere steekproef (bassischoolleerleerlingen uit het eerste, tweede én derde COOL5-18-onderzoek). Het basismodel is weergegeven in figuur 2.1.1.
3.1 Basismodel
In principe is dit hetzelfde model als het model van de huidige po-indicator waarbij we twee verbeteringen hebben doorgevoerd, zoals beschreven in paragraaf 2.1 onder “Stapsgewijze aanpak”. De eerste kolommen van Tabel 3.1.1 bevatten de geschatte coëfficiënten, standaardfouten en p-waardes van de directe effecten op schoolprestaties. Daarnaast hebben we ook de gestandaardiseerde coëfficiënten van dit basismodel en de gestandaardiseerde coëfficiënten van de huidige po-indicator opgenomen.
| Kenmerk | Coefficient | standaardfout | gestandaardiseerde coefficient | Gestandaardiseerde coefficient huidig model | |
|---|---|---|---|---|---|
| Opleidingsniveau vader | 0,82 | 0,03 | < 0,001 | 0,17 | 0,18 |
| Opleidingsniveau moeder | 0,82 | 0,03 | < 0,001 | 0,20 | 0,20 |
| Herkomst | -0,78 | 0,11 | < 0,001 | -0,06 | -0,07 |
| Gemiddeld opleidingsniveau moeders op school | 0,08 | 0,11 | 0,474 | 0,01 | 0,02 |
| Verblijfsduur 0 t/m 5 jaar | 0,54 | 0,48 | 0,257 | 0,01 | 0,00 |
| Verblijfsduur 5 t/m 10 jaar | 1,53 | 0,24 | < 0,001 | 0,04 | 0,04 |
| Schuldsanering | -2,07 | 0,55 | < 0,001 | -0,02 | -0,03 |
Van de variabelen naast intelligentie heeft het opleidingsniveau van de ouders duidelijk de sterkste invloed op Cito-scores in groep 8. Om het gevonden effect van opleidingsniveau in het model uit tabel 3.1.1 te duiden, hebben we in de tabellen 3.1.2 en 3.1.3 de schaalwaarden voor de afzonderlijke opleidingscategorieën van vaders en moeders opgenomen. De positieve directe effecten van de twee opleidingsvariabelen op Cito-score (0,82 voor zowel vaders als moeders) laten zien dat lagere opleidingsniveaus samenhangen met lagere Cito-scores, en hogere opleidingsniveaus met hogere Cito-scores. De vergelijking van de gestandaardiseerde coëfficiënten laat zien dat de invloed van het opleidingsniveau van de vaders in het basismodel licht is afgenomen ten opzichte van de huidige po-indicator.
Naast de invloed van de afzonderlijke opleidingsniveaus – de schaalwaarden – hebben we in de tabellen 3.1.2 en 3.1.3 ter vergelijking ook de schaalwaarden van de huidige po-indicator opgenomen. Hierbij wordt duidelijk dat de verandering in schaalwaarde van de afzonderlijke opleidingsniveaus een groter effect heeft dan de verandering in coëfficiënt van de gehele variabele. Bij zowel vaders als moeders gaat de schaalwaarde van basisonderwijs als hoogste opleidingsniveau verder omlaag. Dit betekent dat – ceteris paribus – de onderwijsscore van kinderen van wie één of beide ouders basisonderwijs als hoogste opleidingsniveau hebben, lager uit zal vallen dan bij de huidige po-indicator. Verder valt op dat bij de vaders de schaalwaarden van de hogere opleidingsniveaus meer en vaker afnemen dan de schaalwaarden van de hogere opleidingsniveaus bij de moeders. Omdat we mbo2 en mbo3 als referentieniveau hebben gebruikt, heeft deze categorie altijd nul als schaalwaarde.
| Schaalwaarde basismodel | Schaalwaarde huidige indicator | |
|---|---|---|
| Basisonderwijs | -2,31 | -2,03 |
| Vmbo-b/k, mbo1 | -1,48 | -1,35 |
| Vmbo-g/t, avo onderbouw | 0,75 | 0,79 |
| Mbo2 en mbo3 | 0,00 | 0,00 |
| Mbo4 | 1,32 | 1,82 |
| Havo, vwo | 3,00 | 3,59 |
| Hbo-, wo-bachelor | 3,51 | 3,49 |
| Hbo-, wo-master, doctor | 4,55 | 4,80 |
| Schaalwaarde basismodel | Schaalwaarde huidige indicator | |
|---|---|---|
| Basisonderwijs | -1,25 | -0,91 |
| Vmbo-b/k, mbo1 | -1,75 | -1,75 |
| Vmbo-g/t, avo onderbouw | 1,15 | 1,43 |
| Mbo2 en mbo3 | 0,00 | 0,00 |
| Mbo4 | 1,78 | 1,74 |
| Havo, vwo | 4,18 | 3,82 |
| Hbo-, wo-bachelor | 4,86 | 4,93 |
| Hbo-, wo-master, doctor | 6,12 | 6,19 |
Tabel 3.1.4 geeft een overzicht van de schaalwaarden voor de herkomstvariabele van het basismodel samen met de vergelijkbare waarden van de huidige po-indicator. Omdat we Nederland als referentieniveau hebben gebruikt, is de schaalwaarde van deze categorie altijd nul.
Ook in deze tabel zijn we verschillende verschuivingen. De meeste schaalwaarden komen dichter bij het referentieniveau te liggen. In het geval van de categorieën Nieuwe EU-landen en economieën in transitie en Overig Afrika, overig Azië, overig Latijns Amerika is deze afname zelfs vrij fors. Oost-Azië is de enige categorie waarvoor de schaalwaarde verder van de referentiecategorie komt te liggen. Doordat de coëfficiënt van de herkomstvariabele negatief is, moeten de schaalwaarden ook omgekeerd worden geïnterpreteerd. Kinderen met Oost-Azië als herkomst krijgen daardoor een hogere onderwijsscore terwijl kinderen uit één van de andere herkomstcategorieën (behalve Nederland) juist een lagere onderwijsscore krijgen op basis van hun herkomst.
| Schaalwaarde basismodel | Schaalwaarde huidige indicator | |
|---|---|---|
| Nederland | 0,00 | 0,00 |
| EU-15, andere ontwikkelde economieën | 1,23 | 1,77 |
| Nieuwe EU-landen en economieën in transitie | 0,02 | 0,85 |
| Noord-Afrika | 0,94 | 1,56 |
| Oost-Azië | -1,04 | -0,73 |
| Overig Afrika, overig Azië, overig Latijns Amerika | 0,57 | 1,44 |
| Suriname en (voormalige) Nederlandse Antillen | 2,61 | 3,09 |
| Turkije | 2,91 | 3,22 |
Deze schaalwaarden worden voorafgaand aan het schatten van het structurele vergelijkingsmodel zelf bepaald uit een lineair regressiemodel voor de Cito-eindtoetsscore waarin alle verklarende variabelen (behalve intelligentie en gemiddeld opleidingsniveau per school) zijn opgenomen. Omdat in zo’n regressiemodel geen onderscheid wordt gemaakt tussen directe en indirecte effecten, is er geen verschil in uitkomsten tussen verschillende structurele vergelijkingsmodellen.
Op basis van de zogenaamde modificatie-indices lijkt het zinvol om modellen te schatten met extra indirecte effecten voor herkomst en het gemiddelde opleidingsniveau van de moeders op school. Zoals we in hoofdstuk 2 hebben aangegeven, kijken we eerst of de theoretische grondslag voor dergelijke modellen wel solide genoeg is. We zijn daarbij tot de conclusie gekomen dat de theoretische onderbouwing voor de gedachte dat land van herkomst en het gemiddelde opleidingsniveau van de moeders van invloed is op de intelligentie te beperkt is om het schatten van dergelijke modellen te rechtvaardigen.
3.2 Vergelijking modellen
In de voorgaande paragraaf hebben we het basismodel gepresenteerd. Op basis van de coëfficiënten lijken deze modellen veel op elkaar. Zoals in hoofdstuk 2 uitgelegd, gebruiken we een drietal fitmaten om de modellen te beoordelen: het AIC, het BIC en de aangepaste R-kwadraat. Deze fitmaten zijn samengevat in tabel 3.3.1. Omdat er geen extra modellen zijn geschat, kunnen we deze ook niet met elkaar vergelijken. Wel kunnen we de aangepaste R-kwadraat vergelijken met de aangepaste R-kwadraat van de huidige po-indicator. Deze is bij het nieuwe model marginaal lager; 0,418 ten opzichte van 0,404. Doordat we de modellen voor de nieuwe indicator en de huidige indicator hebben geschat op (deels) verschillende datasets, kunnen we de AIC, BIC en de loglikelihood niet gebruiken om een vergelijking te maken met de huidige po-indicator.
| AIC | 398 694 |
|---|---|
| BIC | 399 080 |
| Aangepaste R kwadraat | 0,404 |
| Loglikelihood | -199 298 |
Om inzicht te geven hoe dit model zich verhoudt tot de huidige po-indicator, hebben we voor de populatie van het meest recente peilmoment (1 oktober 2020) op basis van dit model ook onderwijsscores uitgerekend. Hierbij hebben we voor de kinderen waarvoor niet direct een onderwijsscore kan worden berekend vanwege het ontbreken van noodzakelijk achtergrondkenmerken, de onderwijsscores geïmputeerd volgens de normale procedure . Vervolgens hebben we de onderwijsscores van de huidige po-indicator vergeleken met deze nieuwe onderwijsscores. In figuur 3.2.2 hebben we deze twee scores tegen elkaar afgezet in een zogenaamde tweedimensionale dichtheidsgrafiek.
3.2.2 Onderwijsscores huidige indicator t.o.v. nieuw model
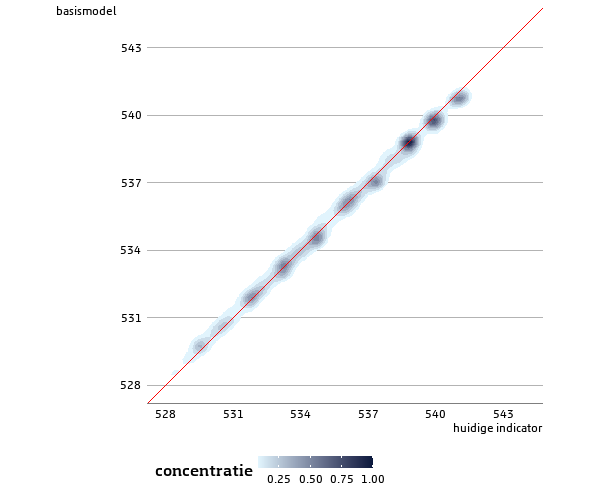
Uit figuur 3.2.2 valt af te leiden dat de onderwijsscores van het nieuwe model altijd in de buurt liggen van de onderwijsscores op basis van de huidige po-indicator. Dit is ook terug te zien in de hoge correlatie tussen deze twee waarden (r = 0,97, p < 0,0001). In tabel 3.2.3 hebben we het verschil tussen deze twee onderwijsscores samengevat. In de gehele populatie ligt de onderwijsscore op basis van het nieuwe model gemiddeld 0,04 punt lager dan in de huidige po-indicator. Voor de kinderen voor wie direct een onderwijsscore kan worden berekend, ligt de verandering in onderwijsscore in 95% van de gevallen tussen de -0,65 en +0,54. Hoewel deze verschillen redelijk klein zijn, kan dit met name voor kinderen met een onderwijsscore rondom de grenswaarde ervoor zorgen dat deze kinderen met het nieuwe model ineens wel of niet tot de doelgroep behoren. Uit de vergelijking van de deelpopulaties – direct bepaalde onderwijsscore of geïmputeerde onderwijsscore – blijkt dat de hoogte van de standaarddeviatie van de gehele populatie fors wordt beïnvloed door de relatief hoge standaarddeviatie van de kinderen voor wie een onderwijsscore wordt geïmputeerd. Op de oorzaak van deze relatief hoge standaarddeviatie gaan we in hoofdstuk 4 dieper in bij het bespreken van de effecten op school- en gemeenteniveau.
| Gemiddeld verschil | Standaard- deviatie | Ondergrens | Bovengrens | |
|---|---|---|---|---|
| Totaal peuters & leerlingen | -0,04 | 0,84 | -1,72 | 1,64 |
| Direct bepaald | -0,06 | 0,3 | -0,65 | 0,54 |
| Geïmputeerd | 0,19 | 3,03 | -5,88 | 6,25 |