3. Herijkingsmethode en resultaten
3.1 Methode
De analysemethode die wordt gebruikt voor de herijking is, net als bij de oorspronkelijke po-indicator en de verkennende herijking uit het eerdere leerplus-rapport, een zogenaamd structureel vergelijkingsmodel. Het basismodel is schematisch weergegeven in Figuur 3.1.1.
Zoals genoemd in paragraaf 2.1 is het doel van de indicator om in beeld te brengen in welke mate kenmerken van de omgeving van leerlingen ermee samenhangen dat zij gemiddeld beter of slechter presteren dan verwacht gezien hun intelligentie. Binnen het structurele vergelijkingsmodel wordt daarom onderscheid gemaakt tussen enerzijds directe effecten van omgevingskenmerken op de schoolprestaties van leerlingen in het vo (de lichtblauwe pijlen in Figuur 3.1.1) en anderzijds indirecte effecten van deze omgevingskenmerken via intelligentie (de rode pijlen). In een indicator voor onderwijsachterstanden in het vo worden uiteindelijk alleen de lichtblauwe pijlen meegenomen: dit zijn namelijk de effecten van omgevingskenmerken die verklaren dat leerlingen met dezelfde aanleg (intelligentie) maar een andere omgeving gemiddeld verschillend presteren in het vo. Nadelige directe effecten van omgevingskenmerken leiden zo tot onderwijsachterstanden. Zie verder het eerste methodologische rapport van de po-indicator voor meer toelichting op het gebruikte model.
3.1.1. Schematische weergave van het structurele vergelijkingsmodel voor onderwijsachterstanden in het vo dat als basis dient voor de herijking van po-indicator
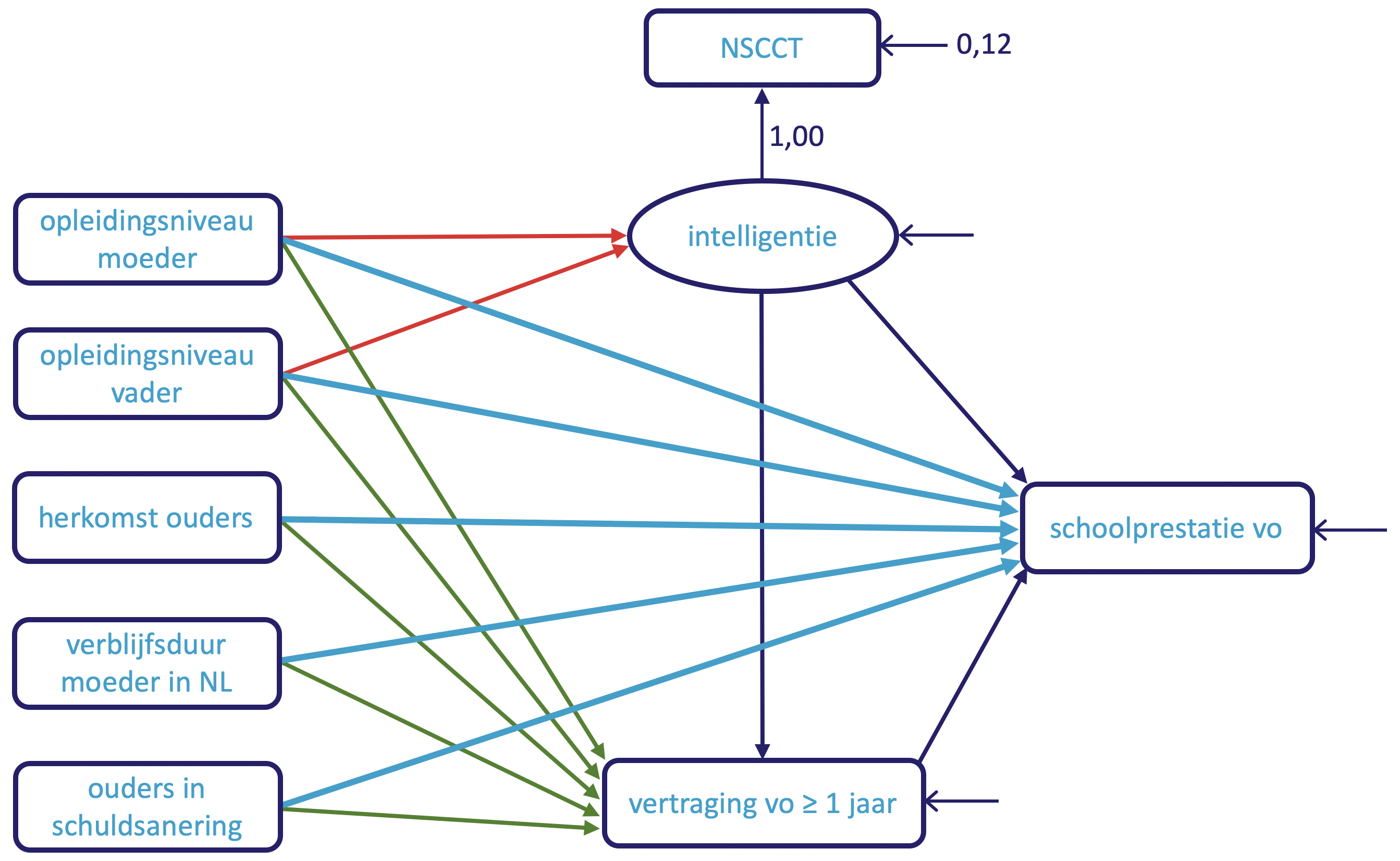
Ten opzichte van het oorspronkelijke model voor de po-indicator en het model voor de verkennende herijking is in het model uit Figuur 3.1.1 een extra kenmerk “vertraging vo” opgenomen om rekening te houden met leerlingen die tijdens hun vo-schoolloopbaan vertraging oplopen, bijvoorbeeld door zittenblijven of als gevolg van een overstap naar een ander onderwijsniveau vóór het eerste eindexamen. Het zou kunnen dat leerlingen die langer naar school gaan in het vo voordat zij voor de eerste keer eindexamen doen gemiddeld hogere cijfers halen dan leerlingen die de nominale looptijd aanhouden. Daarnaast zou het kunnen dat vertraging bij leerlingen met bepaalde omgevingskenmerken vaker voorkomt. Het resultaat zou dan kunnen zijn dat sommige directe effecten van omgevingskenmerken (lichtblauwe pijlen) niet zuiver worden geschat als geen rekening wordt gehouden met vertraging. Door het kenmerk vertraging op te nemen in het model via de extra effecten in Figuur 3.1.1 (groene pijlen) wordt dit gecorrigeerd. Net als intelligentie speelt vertraging in de uiteindelijke herijkte indicator geen rol; dit kenmerk wordt alleen meegenomen om de directe effecten van de andere omgevingskenmerken in de indicator zuiver te kunnen schatten. We maken hierbij alleen onderscheid tussen leerlingen die wel (gecodeerd als 1) of niet (gecodeerd als 0) minimaal één jaar vertraging oplopen gedurende het vo. Leerlingen met twee of meer jaren vertraging en leerlingen met één of meer jaren ‘versnelling’ komen in onze data sporadisch voor, te weinig om voor deze groepen aparte effecten te kunnen schatten.
In Figuur 3.1.1 is met een ovaal aangegeven dat intelligentie niet direct is waargenomen. De waargenomen nscct-score wordt in dit model gezien als een niet-perfecte meting van intelligentie. Zoals beschreven in het eerste methodologische rapport van de po-indicator is uit de literatuur bekend dat de nscct een betrouwbaarheid van 88% heeft voor het meten van intelligentie in groep 5. Bij het schatten van het model is daarom aangenomen dat 12% van de totale variantie in de nscct-scores veroorzaakt wordt door toevallige meetfouten. Verder is geprobeerd te corrigeren voor culturele vertekening van de intelligentiemeting naar opleidingsniveau en herkomst; zie het eerste methodologische rapport van de po-indicator voor meer informatie. In het vervolg beschrijven we alleen aspecten die spelen bij het schatten van het model in het vo die nieuw zijn ten opzichte van de aanpak die is gebruikt bij het schatten van het oorspronkelijke model voor de po-indicator; voor de rest is de aanpak zoals beschreven in het eerste methodologische rapport gevolgd.
Zoals beschreven in paragraaf 2.3 worden de schoolprestaties in het vo hier gemeten door een geordende categoriale variabele, waarbij het aantal categorieën afhangt van het aantal kwantielen van examencijfers dat wordt meegenomen. Om het model uit Figuur 3.1.1 op een valide manier te schatten moeten de categorieën van deze variabele worden afgebeeld op een intervalschaal. Dit laatste betekent dat de schaalwaarden die aan de categorieën hangen de volgende interpretatie hebben: als de categorieën A en B twee keer zover uit elkaar liggen als de categorieën B en C, dan is het verschil in schoolprestatie tussen categorie A en B ook twee keer zo groot als het verschil tussen categorie B en C. Als we de categorieën eenvoudig zouden nummeren als 1, 2, 3, …, hoort hierbij dus de impliciete aanname dat alle categorieën even ver uit elkaar liggen: de afstand tussen “Praktijkonderwijs” en “Vmbo-basisberoeps, eerste kwantiel” is even groot als die tussen “Vmbo-basisberoeps, eerste kwantiel” en “Vmbo-basisberoeps, tweede kwantiel”, enzovoort. Het is niet op voorhand duidelijk of dit een zinnige aanname is. Algemener is niet duidelijk wat de beste manier is om de schaalwaarden te kiezen in lijn met deze interpretatie.
Bij de herijking uit het eerdere leerplus-rapport (op basis van alleen onderwijsniveau) speelde dezelfde vraag. Er zijn toen twee varianten onderzocht:
- gebruik de gemiddelde score op de Cito-eindtoets in groep 8 van alle leerlingen in een bepaalde categorie als schaalwaarde voor die categorie, of
- gebruik een automatische procedure om, als onderdeel van het schatten van het model, schaalwaarden toe te kennen aan de categorieën zodat de verklaarde variantie van de schoolprestaties door het model maximaal is (“optimaal schalen”).
Een klein praktisch voordeel van de eerste variant is dat de categorieën worden afgebeeld op een vergelijkbare schaal als de Cito-score waarop de po-indicator is gebaseerd (d.w.z. waarden tussen 501 en 550). Dit maakt een vergelijking tussen de indicator vóór en na herijken iets eenvoudiger. Bij de tweede variant liggen de schaalwaarden rondom 0.
Beide varianten zijn ook in dit onderzoek uitgeprobeerd. Bij de eerste variant bleek dat de gemiddelde Cito-eindtoetsscore vooral verschilt tussen de onderwijsniveaus maar nauwelijks tussen de examenkwantielen binnen een onderwijsniveau. De uitkomsten van een verkennende analyse bij deze variant leken daarom sterk op die uit de eerdere herijking, waarbij alleen naar onderwijsniveau is gekeken. Aangezien we in het huidige onderzoek juist een verfijning willen aanbrengen in de meting van schoolprestaties binnen onderwijsniveaus, is daarom besloten om alleen verder te gaan met de tweede variant.
3.2 Resultaten
Bij het schatten van het model uit Figuur 3.1.1 moet nog een aantal keuzes worden gemaakt. We hebben de invloed op de uitkomsten onderzocht van de volgende keuzes:
- Aantal kwantielen examencijfers: drie, vier of vijf kwantielen meegenomen.
- Ordening van de categorieën: het hoogste kwantiel binnen onderwijsniveau X komt in de ordening vóór of na het laagste kwantiel binnen onderwijsniveau X + 1. In het eerste geval (“niet herordenen”) worden de examencijfers alleen gebruikt om de onderwijsniveaus nader te detailleren (waarbij, bijvoorbeeld, een vwo-niveau altijd wordt gezien als een betere prestatie dan een havo-niveau). In het tweede geval (“wel herordenen”) wordt het behalen van een van de hoogste examencijfers op een bepaald onderwijsniveau gezien als een betere prestatie dan het behalen van een van de laagste examencijfers op het volgende onderwijsniveau.
- Vertraging wel of niet opnemen in het model.
- Gemiddeld opleidingsniveau moeders per school wel of niet opnemen in het model. Een aanleiding om apart naar dit kenmerk te kijken is dat de interpretatie van dit kenmerk in een voor het vo herijkte indicator verschilt van de oorspronkelijke po-indicator (zie paragraaf 2.2).
We presenteren eerst de modeluitkomsten bij de volgende combinatie van keuzes: vijf kwantielen, niet herordenen, vertraging wel in het model, gemiddeld opleidingsniveau niet in het model. Daarna bespreken we het effect van andere keuzes op deze uitkomsten.
3.2.1 Resultaten basismodel
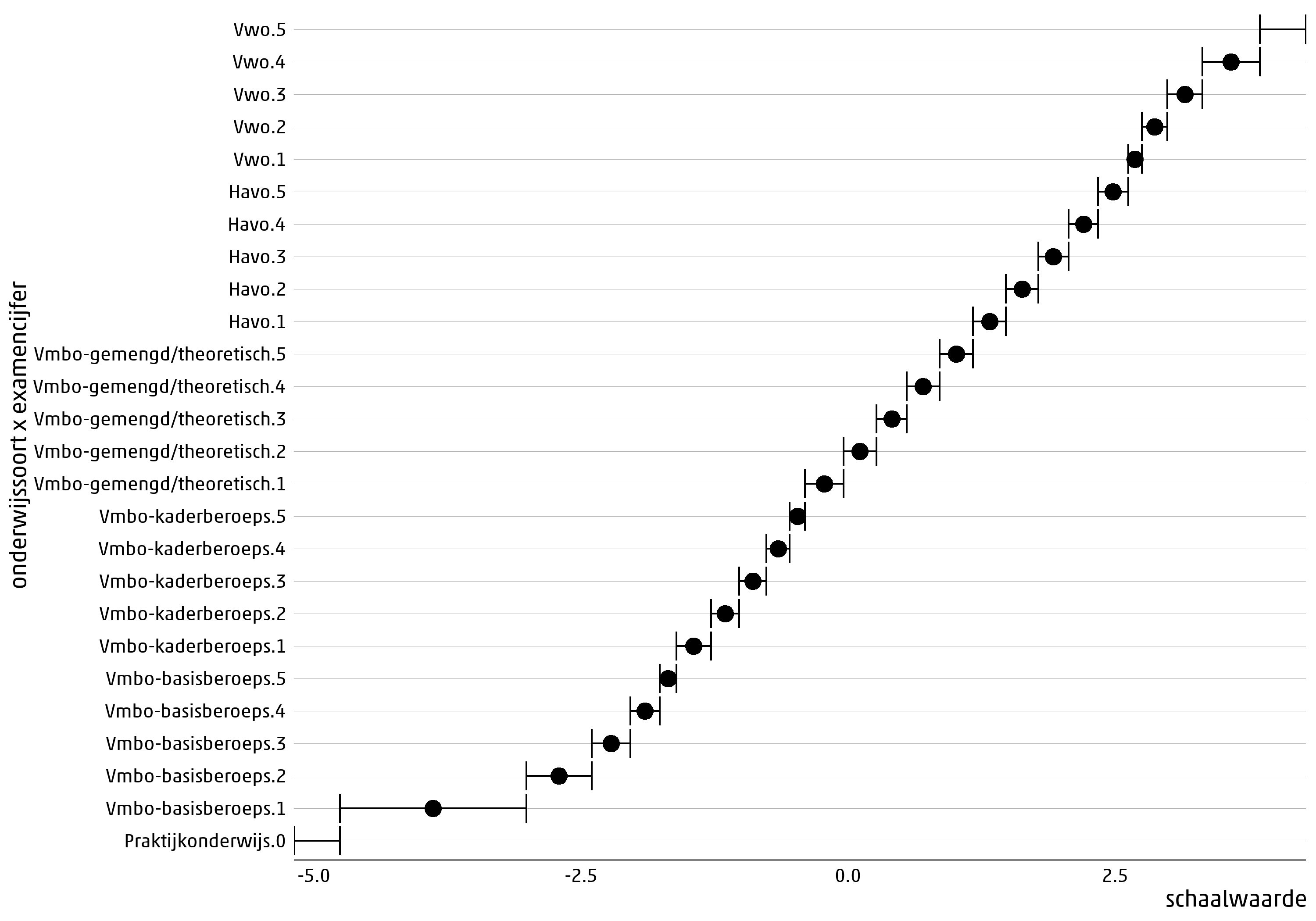
Figuur 3.2.1.1 toont de schaalwaarden van de 26 categorieën van schoolprestatie na “optimaal schalen” bij dit model. Door de automatische procedure is aan alle categorieën behalve de eerste en laatste een interval van schaalwaarden toegewezen; het middelpunt van elk interval is in de figuur aangegeven met een stip. Bij de eerste categorie horen alle schaalwaarden links van het eerste interval en bij de laatste categorie horen alle schaalwaarden rechts van het laatste interval. In de figuur is te zien dat de opeenvolgende categorieën grotendeels gelijkmatig zijn verdeeld over de schaal; alleen aan de onderkant en, in mindere mate, aan de bovenkant van de verdeling zijn de afstanden tussen de categorieën groter.
3.2.1.1 Categorieën van schoolprestatie in het vo (examencijfers in vijf kwantielen, niet herordenen) op een numerieke schaal, volgens “optimaal schalen"
Tabel 3.2.1.2 toont de geschatte directe effecten op schoolprestaties in het vo bij dit model. Voor opleidingsniveau en herkomst bevat het model verder aparte schaalwaarden per categorie; de schattingen van deze schaalwaarden staan in Tabel 3.2.1.3 en Tabel 3.2.1.4.
De eerste kolommen van Tabel 3.2.1.2 bevatten de geschatte coëfficiënten, standaardfouten en p-waardes van de directe effecten op schoolprestaties in het vo. De p-waarde is in dit geval de kans dat de geschatte coëfficiënt ook zou kunnen zijn gevonden als de werkelijke coëfficiënt gelijk is aan 0, gezien de bijbehorende standaardfout. Het blijkt dat alle kenmerken in het model een effect hebben dat significant van 0 verschilt. Bij verblijfsduur moeder verschilt de categorie “0-5 jaar” niet significant van de referentiecategorie (“10 jaar of langer”), maar de categorie “5-10 jaar” wel. De gevonden effecten van dit kenmerk in het vo zijn vergelijkbaar met de eerder gevonden effecten in het po; zie het eerste methodologische rapport van de po-indicator voor een bespreking van deze effecten. Vertraging heeft een licht-significant effect in de richting die we verwachtten: leerlingen die langer dan de nominale looptijd op een vo-school zitten voordat zij voor het eerst eindexamen doen presteren, gegeven alle andere kenmerken uit het model, gemiddeld iets beter.
Om het relatieve belang van de verschillende kenmerken onderling te vergelijken toont Tabel 3.2.1.2 ook de gestandaardiseerde coëfficiënten. Ter vergelijking zijn tevens de gestandaardiseerde coëfficiënten uit de oorspronkelijke po-indicator opgenomen in de tabel (laatste kolom). Te zien is dat het effect van intelligentie op schoolprestaties in het vo zwakker is dan in het po, terwijl het effect van de omgevingskenmerken, met name opleidingsniveau en herkomstgroepering, juist sterker is in het vo. Een gedeeltelijke verklaring voor deze sterkere invloed van de omgeving is dat we nu kijken naar schoolprestaties op latere leeftijd. De effecten van de achtergrondkenmerken op onderwijsachterstanden zijn al zichtbaar bij de overgang van po naar vo en werken daarna verder door gedurende het vo. Hierbij moet wel worden opgemerkt dat we schoolprestaties in het vo (noodgedwongen) hebben gemeten op een andere manier dan in het po, wat een gedetailleerde inhoudelijke vergelijking van de gevonden effecten tussen de twee modellen lastig maakt.
| Kenmerk | Coëfficiënt | Std.fout | P-waarde | Std.coëf. | Std.coëf. po |
|---|---|---|---|---|---|
| Opleidingsniveau vader | 0,95 | 0,04 | < 0,001 | 0,33 | 0,18 |
| Opleidingsniveau moeder | 0,95 | 0,03 | < 0,001 | 0,37 | 0,20 |
| Herkomst | –0,99 | 0,10 | < 0,001 | –0,11 | –0,07 |
| Verblijfsduur moeder: 0-5 jaar | –0,06 | 0,12 | 0,59 | –0,01 | 0,00 |
| Verblijfsduur moeder: 5-10 jaar | 0,29 | 0,06 | < 0,001 | 0,05 | 0,03 |
| Ouders wel in schuldsanering | –0,84 | 0,14 | < 0,001 | –0,07 | –0,03 |
| Intelligentie | 0,34 | 0,01 | < 0,001 | 0,22 | 0,48 |
| Vertraging vo ≥1 jaar | 0,04 | 0,02 | 0,01 | 0,01 | - |
| Categorie | Opleidingsniveau vader, schaalwaarde | Opleidingsniveau vader, std.fout | Opleidingsniveau moeder, schaalwaarde | Opleidingsniveau moeder, std.fout |
|---|---|---|---|---|
| Basisonderwijs | –0,23 | 0,06 | –0,35 | 0,07 |
| Vmbo-b/k, mbo1 | –0,15 | 0,05 | –0,32 | 0,06 |
| Vmbo-g/t, avo onderbouw | 0,22 | 0,08 | 0,15 | 0,07 |
| Mbo2, mbo3 (referentiecat.) | 0,00 | - | 0,00 | - |
| Mbo4 | 0,42 | 0,05 | 0,34 | 0,05 |
| Havo, vwo | 0,67 | 0,07 | 0,66 | 0,06 |
| Hbo-, wo-bachelor | 0,87 | 0,06 | 1,07 | 0,06 |
| Hbo-, wo-master, doctor | 1,29 | 0,07 | 1,34 | 0,08 |
| Categorie | Schaalwaarde | Std.fout |
|---|---|---|
| Nederland (referentiecat.) | 0,00 | - |
| EU-15, andere ontwikkelde economieën | 0,12 | 0,16 |
| Nieuwe EU-landen, economieën in transitie | 0,14 | 0,15 |
| Noord-Afrika | 0,16 | 0,07 |
| Oost-Azië | –0,48 | 0,14 |
| Rest Afrika, rest Azië, rest Latijns Amerika | 0,02 | 0,11 |
| Suriname en (voormalige) Nederlandse Antillen | 0,49 | 0,10 |
| Turkije | 0,49 | 0,07 |
De verklaarde variantie in schoolprestaties in het vo is bij dit model 50,2%. Ter vergelijking: het model waarop de po-indicator is gebaseerd verklaarde 41,3% van de variantie in schoolprestaties in het po (zie het eerste methodologische rapport van de po-indicator). De verklaarde variantie in het vo bij de eerdere verkennende herijking was 37,2%. Door informatie over individuele verschillen in schoolprestaties binnen onderwijsniveaus toe te voegen aan de te verklaren variabele, kan door de omgevingskenmerken in het model dus meer van de variantie in schoolprestaties worden verklaard.
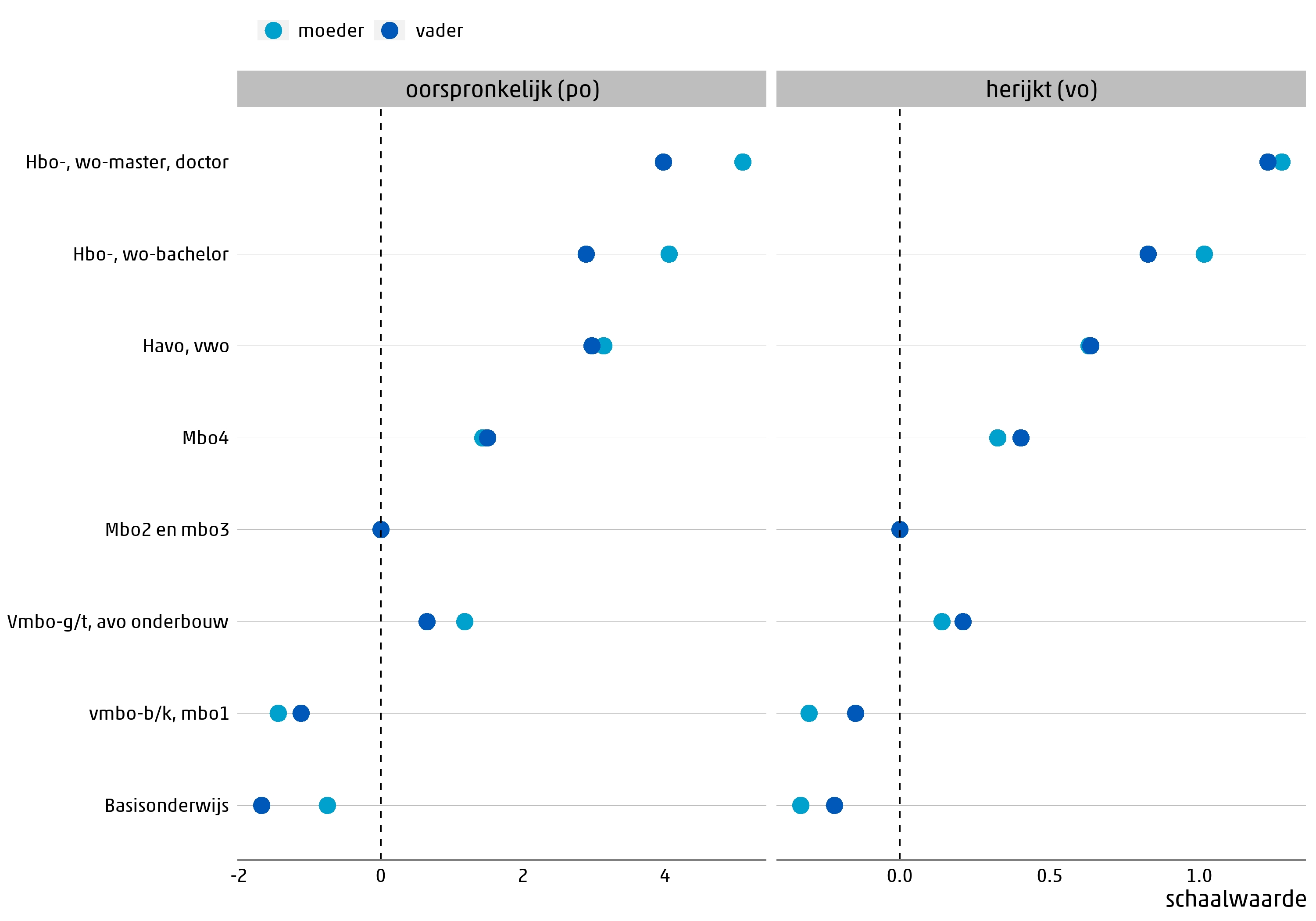
3.2.1.5 Totale bijdrage per categorie van herkomstgroepering aan de oorspronkelijke po-indicator en de herijkte vo-indicator
3.2.1.6 Totale bijdrage per categorie van herkomstgroepering aan de oorspronkelijke po-indicator en de herijkte vo-indicator
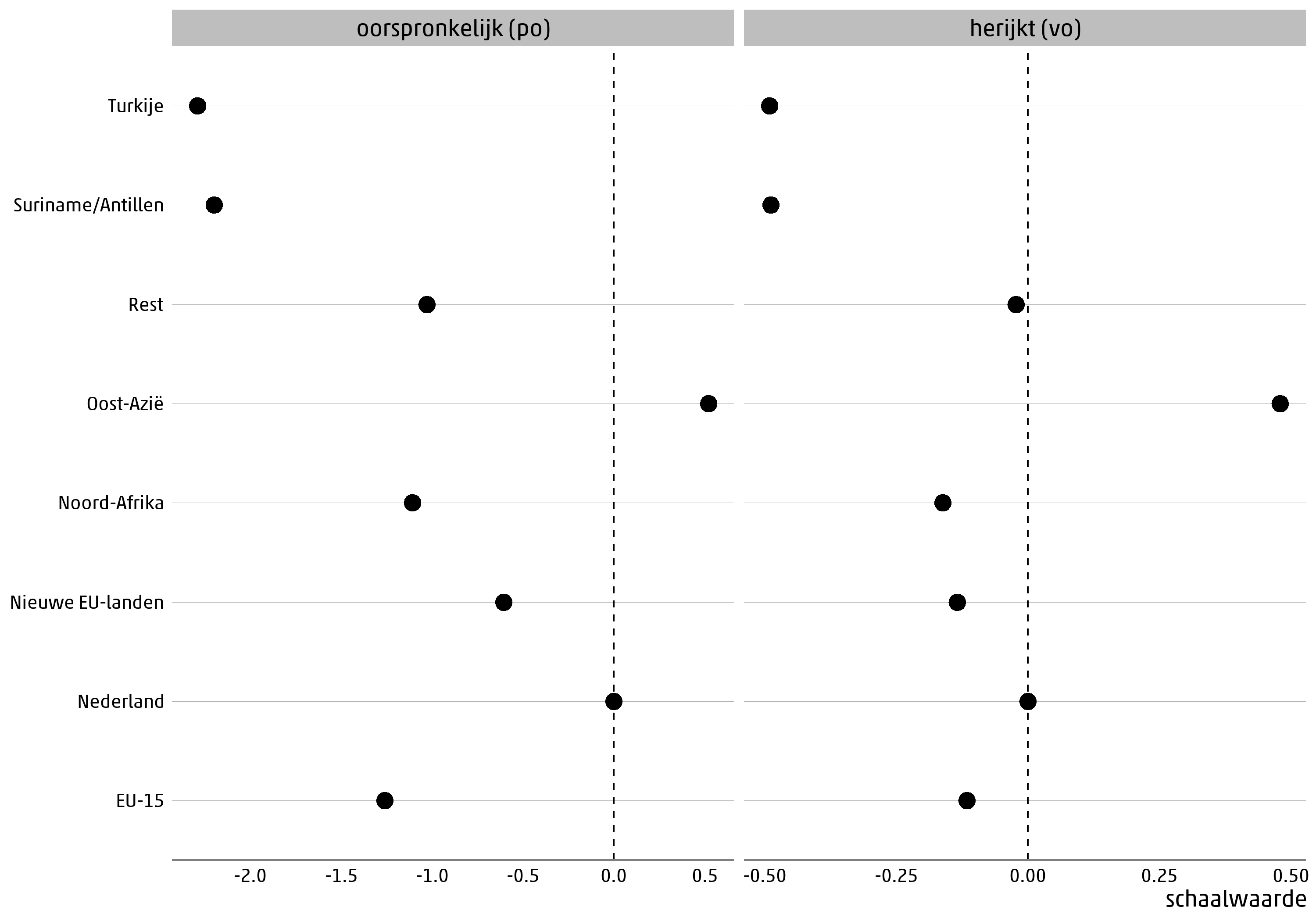
Om de bijdrage van een afzonderlijke categorie van opleidingsniveau of herkomstgroepering aan de herijkte indicator te vinden moet de coëfficiënt uit Tabel 3.2.1.2 worden vermenigvuldigd met de schaalwaarde van die categorie uit Tabel 3.2.1.3 of Tabel 3.2.1.4. Bijvoorbeeld: de totale bijdrage van de categorie “Hbo-, wo-master, doctor” van het kenmerk opleidingsniveau vader is 0,95 × 1,29 = 1,23. De resulterende bijdragen van alle categorieën zijn weergegeven in Figuur 3.2.1.5 (opleidingsniveau vader en moeder) en Figuur 3.2.1.6 (herkomst). Ter vergelijking worden ook de overeenkomstige bijdragen uit de po-indicator getoond. Merk op: de bijdragen met en zonder herijking liggen op verschillende schalen, en de absolute waarden van deze bijdragen zijn daarom niet direct met elkaar te vergelijken. Wel kan het patroon over de categorieën in deze figuren worden vergeleken.
In Figuur 3.2.1.5 is in grote lijnen hetzelfde patroon te zien in de bijdragen van de categorieën van beide opleidingsniveau-kenmerken vóór en na herijking. Een soortgelijke uitkomst werd ook gevonden bij de eerdere verkennende herijking (zie het eerdere leerplus-rapport). Voor zover er iets verandert kunnen we stellen dat de bijdragen van vader en moeder bij de laagste en hoogste opleidingsniveaus iets dichter bij elkaar liggen na herijking voor het vo.
Bij herkomstgroepering in Figuur 3.2.1.6 zijn grotere verschillen te zien tussen wel en niet herijken. Ten opzichte van de referentiecategorie “Nederland” zijn de bijdragen van de andere categorieën na de herijking iets opgeschoven naar rechts. Dat wil zeggen: de effecten van deze categorieën op schoolprestaties zijn in het vo minder negatief (in het geval van “Oost-Azië”: meer positief) dan in het po. Met name bij “Suriname en (voormalige) Nederlandse Antillen” en “Turkije” blijft wel een duidelijk negatief effect op schoolprestaties in het vo zichtbaar.
Bij de verkennende herijking op basis van alleen het onderwijsniveau (zie het eerdere leerplus-rapport) werd voor de schaalwaarden van herkomstgroepering een nog sterkere verschuiving in dezelfde richting gevonden. Door rekening te houden met individuele verschillen in schoolprestaties binnen een onderwijsniveau wordt dit resultaat nu genuanceerd: de verschillen in onderwijsachterstanden tussen herkomstgroeperingen zijn in het vo weliswaar minder groot dan in het po, maar bij bepaalde herkomstgroeperingen komen nog steeds duidelijk meer onderwijsachterstanden voor dan bij de referentiecategorie “Nederland”.
Tabel 3.2.1.7 toont de geschatte coëfficiënten van de directe effecten van omgevingskenmerken op vertraging in het vo (de groene pijlen in Figuur 3.1.1). Te zien is dat de meeste kenmerken geen significant effect hebben op vertraging. Alleen bij herkomstgroepering vinden we een licht-significant effect. Al met al lijkt het percentage kinderen dat één of meer jaren vertraging oploopt in het vo tamelijk gelijkmatig verdeeld te zijn naar de achtergrondkenmerken die in dit model zijn opgenomen.
| Kenmerk | Coëfficiënt | Std.fout | P-waarde |
|---|---|---|---|
| Constante | 0,16 | 0,11 | 0,13 |
| Opleidingsniveau vader | 0,00 | 0,01 | 0,81 |
| Opleidingsniveau moeder | 0,01 | 0,01 | 0,19 |
| Herkomst | 0,07 | 0,03 | 0,02 |
| Verblijfsduur moeder: 0-5 jaar | –0,01 | 0,03 | 0,60 |
| Verblijfsduur moeder: 5-10 jaar | –0,00 | 0,01 | 0,96 |
| Ouders wel in schuldsanering | –0,03 | 0,03 | 0,41 |
| Intelligentie | 0,01 | 0,00 | 0,18 |
3.2.2 Resultaten voor modellen met andere aantallen kwantielen en/of ordening
Het model uit paragraaf 3.2.1 is ook geschat voor vier alternatieve varianten van de te verklaren variabele schoolprestatie in het vo:
- drie kwantielen van examencijfers onderscheiden, categorieën niet herordend zoals beschreven aan het begin van paragraaf 3.2;
- drie kwantielen van examencijfers onderscheiden, categorieën wel herordend;
- vier kwantielen van examencijfers onderscheiden, categorieën niet herordend;
- vier kwantielen van examencijfers onderscheiden, categorieën wel herordend.
Tabel 3.2.2.1 toont de geschatte directe effecten van omgevingskenmerken op schoolprestaties volgens deze alternatieve indelingen. Ter vergelijking bevat de laatste kolom nogmaals de geschatte directe effecten uit Tabel 3.2.1.2. Te zien is dat de gevonden coëfficiënten nauwelijks verschillen tussen de vijf varianten. Ook de vorm van de verdeling van “optimaal geschaalde” schoolprestaties zoals in Figuur 3.2.1.1, de schaalwaarden van opleidingsniveau en herkomst zoals in Tabel 3.2.1.3 en Tabel 3.2.1.4 en de geschatte directe effecten van omgevingskenmerken op vertraging zoals in Tabel 3.2.1.7 zijn bij alle varianten nagenoeg hetzelfde (hier niet getoond).
De verklaarde varianties zijn bij de modellen uit Tabel 3.2.2.1 respectievelijk gelijk aan 50,3%, 48,3%, 50,4%, 49,8% en 50,2%. Ook in dit opzicht zijn de verschillen dus klein, zij het dat de verklaarde variantie iets lager is als de volgorde van de categorieën wordt aangepast.
| Kenmerk | Coëfficiënt (3, niet herordenen) | Coëfficiënt (3, wel herordenen) | Coëfficiënt (4, niet herordenen) | Coëfficiënt (4, wel herordenen) | Coëfficiënt (5, niet herordenen) |
|---|---|---|---|---|---|
| Opleidingsniveau vader | 0,95 | 0,95 | 0,95 | 0,95 | 0,95 |
| Opleidingsniveau moeder | 0,95 | 0,95 | 0,95 | 0,95 | 0,95 |
| Herkomst | –0,99 | –1,00 | –0,99 | –0,99 | –0,99 |
| Verblijfsduur moeder: 0-5 jaar | –0,07 | –0,05 | –0,03 | –0,01 | –0,06 |
| Verblijfsduur moeder: 5-10 jaar | 0,29 | 0,29 | 0,30 | 0,29 | 0,29 |
| Ouders wel in schuldsanering | –0,83 | –0,83 | –0,84 | –0,84 | –0,84 |
| Intelligentie | 0,36 | 0,34 | 0,35 | 0,35 | 0,34 |
| Vertraging vo ≥1 jaar | 0,05 | 0,02 | 0,05 | 0,03 | 0,04 |
3.2.3 Resultaten voor modellen zonder vertraging
De vijf varianten van het model uit Tabel 3.2.2.1 zijn ook geschat zonder dat vertraging is opgenomen in het model. Ook hier waren de verschillen in de modeluitkomsten steeds zeer klein. Gezien de beperkte invloed van vertraging op schoolprestaties en de zwakke samenhang met de andere omgevingskenmerken die zijn gevonden in paragraaf 3.2.1 is dit niet onverwacht. Kortheidshalve tonen we in Tabel 3.2.3.1 alleen de geschatte directe effecten bij een indeling met vijf kwantielen, met en zonder vertraging in het model. De verklaarde variantie van schoolprestaties in het vo is bij beide modellen 50,2%.
| Kenmerk | Coëfficiënt (zonder vertraging) | Coëfficiënt (met vertraging) |
|---|---|---|
| Opleidingsniveau vader | 0,95 | 0,95 |
| Opleidingsniveau moeder | 0,95 | 0,95 |
| Herkomst | –1,00 | –0,99 |
| Verblijfsduur moeder: 0-5 jaar | –0,06 | –0,06 |
| Verblijfsduur moeder: 5-10 jaar | 0,28 | 0,29 |
| Ouders wel in schuldsanering | –0,84 | –0,84 |
| Intelligentie | 0,34 | 0,34 |
| Vertraging vo ≥1 jaar | - | 0,04 |
3.2.4 Resultaten voor modellen met gemiddeld opleidingsniveau moeders op school
Ten slotte bekijken we de invloed van het meenemen van het kenmerk gemiddeld opleidingsniveau moeders op school op de modeluitkomsten. Net als bij de po-indicator wordt dit kenmerk berekend door het gemiddelde te nemen van het opleidingsniveau van alle moeders op een school, gebruikmakend van de schaalwaarden voor opleidingsniveau moeder zoals in Tabel 3.2.1.3. Bij de herijkte indicator gaat het om de vo-school in plaats van de po-school waarop een leerling zit. Ook deze analyse is gedaan voor alle vijf de varianten van het model uit Tabel 3.2.2.1, met zeer vergelijkbare uitkomsten; we beperken ons hier opnieuw tot het bespreken van de variant met examencijfers in vijf kwantielen.
| Kenmerk | Coëfficiënt (met gem. opleidingsniveau) | Coëfficiënt (zonder gem. opleidingsniveau) |
|---|---|---|
| Opleidingsniveau vader | 0,85 | 0,95 |
| Opleidingsniveau moeder | 0,78 | 0,95 |
| Herkomst | –0,48 | –0,99 |
| Verblijfsduur moeder: 0-5 jaar | 0,01 | –0,06 |
| Verblijfsduur moeder: 5-10 jaar | 0,35 | 0,29 |
| Ouders wel in schuldsanering | –0,77 | –0,84 |
| Gemiddeld opleidingsniveau moeders op vo-school | 3,10 | - |
| Intelligentie | 0,33 | 0,34 |
| Vertraging vo ≥1 jaar | 0,05 | 0,04 |
Tabel 3.2.4.1 toont de geschatte directe effecten van omgevingskenmerken op schoolprestaties in het vo voor het model met en zonder gemiddeld opleidingsniveau van moeders op school. Het toevoegen van dit kenmerk aan het model leidt tot een verschuiving in sommige coëfficiënten: met name de effecten van opleidingsniveau en herkomstgroepering worden minder sterk. Bovendien blijkt het gemiddeld opleidingsniveau een zeer sterk effect te hebben op de gemeten schoolprestaties. De verklaarde variantie van het model stijgt hierdoor van 50,2% naar 57,2%.
Deze sterke samenhang tussen gemiddeld opleidingsniveau en schoolprestaties lijkt echter vooral een artefact te zijn van de manier waarop schoolprestaties hier zijn gemeten. Het onderwijsniveau waarop een leerling examen doet is sterk bepalend voor zijn/haar positie op de gekozen schaal (zie Figuur 3.2.1.1). Tegelijk zien we in de data een duidelijk verband tussen het gemiddeld opleidingsniveau van moeders van leerlingen per onderwijsniveau (zie Tabel 3.2.4.2): hoe hoger het onderwijsniveau, des te hoger is het gemiddeld opleidingsniveau van de moeders. Hierbij moet ook worden bedacht dat op veel scholen maar een deel van alle mogelijke onderwijsniveaus wordt gegeven, zodat op deze scholen slechts een deel van het theoretische bereik van schoolprestaties uit Figuur 3.2.1.1 feitelijk voorkomt. Statistisch is het daarom begrijpelijk dat uit het geschatte model volgt dat het gemiddeld opleidingsniveau van moeders per school een goed verklarend kenmerk is voor schoolprestaties: het gemiddeld opleidingsniveau van alle moeders op een school is in feite een vrij goede proxy voor de combinatie van onderwijsniveaus die op die school worden gegeven en daarmee voor schoolprestaties zoals gemeten op de hier gebruikte schaal. Het verband dat we op deze manier vinden lijkt echter geen inhoudelijke verklaring te zijn voor werkelijke verschillen in onderwijsachterstanden tussen scholen. Het model zonder dit kenmerk lijkt daarom een betrouwbaardere basis voor een indicator voor onderwijsachterstanden in het vo.
| Onderwijsniveau | Gemiddeld opleidingsniveau moeders |
|---|---|
| Praktijkonderwijs | –0,01 |
| Vmbo-basisberoeps | 0,23 |
| Vmbo-kaderberoeps | 0,25 |
| Vmbo-gemengd/theoretisch | 0,31 |
| Havo | 0,36 |
| Vwo | 0,43 |