3. Ontwikkeling model voor het vo
3.1 Inleiding
In dit hoofdstuk bespreken we de totstandkoming van het model waarmee voor het vo op leerlingniveau de kans op voortijdig schoolverlaten (vsv) kan worden geschat volgens de aanpak zoals beschreven in paragraaf 2.7. De eerste stap betreft de selectie van achtergrondkenmerken op basis van beschrijvende en bivariate analyses. In de tweede stap wordt een stepwise selectieprocedure toegepast op het cohort 2018/’19 en op het validatiecohort 2017/’18. Vervolgens bespreken we in de derde stap de resultaten van de kruisvalidaties. Bovendien onderzoeken we in de vierde stap of het model met multilevel-component toegevoegde waarde heeft. Tot slot presenteren we in de laatste paragraaf een vergelijking van de modelschattingen op basis van een DUO-cohort en een eerste beeld van de resultaten op het niveau van RMC-regio.
3.2 Stap 1: Voorselectie kenmerken
Om het effect van de achtergrondkenmerken, zoals beschreven in paragraaf 2.5, te onderzoeken is er een voorselectie gemaakt op basis van beschrijvende statistieken en bivariate analyses. Op basis van deze analyses zijn er keuzes gemaakt in de codering van de variabelen, zijn referentiecategorieën bepaald en is een keuze gemaakt bij (inhoudelijk) vergelijkbare kenmerken.
De belangrijkste wijzigingen zijn hier uitgelicht:
- Ongeoorloofd verzuim: Vsv kwam zeer beperkt voor in de groep leerlingen die doorverwezen was naar Halt wegens overtreding van de leerplicht. Dit is niet wenselijk bij het uitvoeren van regressieanalyses, omdat dit kan leiden tot onbetrouwbare en moeilijk te interpreteren resultaten. Het kenmerk is daarom niet meegenomen in de verdere analyses.
- Huishoudinkomen onder de lage inkomensgrens: Dit kenmerk overlapt sterk met de welvaartspercentielen, waardoor we, op advies van een inhoudelijk expert van het CBS, uiteindelijk ervoor hebben gekozen om de welvaartspercentielen mee te nemen in de verdere analyses in plaats van deze variabele. Dit kenmerk bevat daarnaast alleen inkomen, terwijl de welvaartspercentielen ook rekening houden met het vermogen. Hetzelfde geldt voor het kenmerk op buurtniveau.
- Lage welvaart in het huishouden: Omdat de welvaartspercentielen in vijf categorieën een vollediger beeld geven dan alleen het laagste percentiel, is er voor gekozen de lage welvaart niet mee te nemen in de verdere analyses.
- Aantal gewerkte uren: Het hebben van een bijbaan kan – theoretisch gezien – de kans op vsv zowel vergroten als verkleinen. Dit kenmerk is daarom lastig te interpreteren en werkelijke effecten kunnen daardoor vertekend zijn. Daarom is besloten dit kenmerk niet mee te nemen in verdere analyses.
- Problematische schulden: Vo-leerlingen hebben zelf meestal geen geregistreerde problematische schulden binnen de definitie zoals beschreven in bijlage 3. Daarom nemen we enkel de schulden op huishoudniveau mee voor het vo. Dit betekent dat de indeling van dit kenmerk is aangepast voor het vo naar twee categorieën: geen problematische schulden (0) en wel problematische schulden (1) in het huishouden.
3.3 Stap 2: Stepwise analyse
Na de voorselectie van kenmerken is er een stepwise procedure toegepast om de kenmerken te selecteren die het beste model vormen. Dit is gedaan met de forward en backward search en een combinatie van beiden. Uiteindelijk zijn de modelschattingen van de methoden vergeleken. Het doel is om een compact model over te houden, met voldoende verklaringskracht. Waar de forward methode kenmerken stapsgewijs toevoegt, verwijdert de backward methode deze stapsgewijs. De forward methode stopt als er geen modelverbetering meer optreedt op basis van de BIC-waarde. De backward methode doet hetzelfde bij het verwijderen van de kenmerken. De forward methode leverde in de analyses een compactere selectie kenmerken op dan de backward methode, waardoor deze stepwise methode als uitgangspunt is genomen voor de verdere selectie van kenmerken. Bovendien lagen zowel de BIC als de pseudo-R2-maten voor beide methoden dicht bij elkaar (forward: BIC = 60 846, McKelveyZavoina R2 = 0,37; backward: BIC = 60 828, McKelveyZavoina R2 = 0,37).
De forward analyse resulteerde in de volgende selectie van kenmerken, in volgorde van toegevoegde waarde voor het model:
- Leeftijd
- Onderwijssoort
- Psychosociale problemen leerling
- Vertraging
- Welvaart huishouden
- Ouderlijke structuur
- Verdacht van misdrijf
- Geslacht
- Problematische schulden in huishouden
- Hoogst behaalde opleidingsniveau moeder
- Langdurige gezondheidsproblemen
Na de selectie van het elfde kenmerk stopte de stepwise procedure, omdat er volgens het model geen extra verklaringskracht meer werd toegevoegd.
De forward methode voegt telkens één kenmerk toe aan het model. Per stap in deze methode is de BIC uitgerekend om te bepalen in hoeverre er nog modelverbetering optreedt, zie figuur 3.3.1. Hierbij geldt dat een lagere BIC-waarde een betere modelkwaliteit betekent.
| volgorde | BIC (BIC-waarde) |
|---|---|
| 0 | 86574 |
| 1 | 68599 |
| 2 | 62958 |
| 3 | 62259 |
| 4 | 61799 |
| 5 | 61430 |
| 6 | 61189 |
| 7 | 61016 |
| 8 | 60941 |
| 9 | 60882 |
| 10 | 60860 |
| 11 | 60846 |
De figuur laat zien dat hoe meer kenmerken er worden opgenomen, hoe lager de BIC wordt en des te beter het totale model de kans op vsv dus kan schatten. De grootste afname van de BIC ligt bij het eerste kenmerk: leeftijd van de leerling voegt dus het meeste toe aan het model. Ook het tweede kenmerk, de onderwijssoort die de leerling volgt, voegt veel toe aan het model. Na het zevende kenmerk is de daling van de BIC beperkt (minder dan 100); de modelkwaliteit neemt bij het toevoegen van de laatste kenmerken nauwelijks nog toe.
Daarnaast is de stabiliteit van het model onderzocht door de forward stepwise procedure toe te passen op het validatiecohort (2017/’18). Er is dus opnieuw een stepwise procedure toegepast, waarbij opnieuw bepaald werd welke modelkenmerken relevant zijn voor dat cohort. Bij het validatiecohort stopte de stepwise procedure na twaalf kenmerken. Vervolgens konden de geselecteerde kenmerken en hun volgorde vergeleken worden tussen de twee cohorten. De resultaten worden weergegeven in tabel 3.3.2.
| Volgorde | Basiscohort (2018/’19) | Validatiecohort (2017/’18) |
|---|---|---|
| 1 | Leeftijd | Leeftijd |
| 2 | Onderwijssoort | Onderwijssoort |
| 3 | Psychosociale problemen | Psychosociale problemen |
| 4 | Vertraging | Welvaart huishouden |
| 5 | Welvaart huishouden | Vertraging |
| 6 | Ouderlijke structuur | Ouderlijke structuur |
| 7 | Verdacht van misdrijf | Verdacht van misdrijf |
| 8 | Geslacht | Problematische schulden in huishouden |
| 9 | Problematische schulden in huishouden | Geslacht |
| 10 | Hoogst behaalde opleidingsniveau moeder | Hoogst behaalde opleidingsniveau moeder |
| 11 | Langdurige gezondheidsproblemen | Verblijfsduur moeder in Nederland |
| 12 | Acute gezondheidsproblemen | |
In figuur 3.3.1. werd duidelijk dat een model met zeven kenmerken de voorkeur had indien naar de BIC-waarden gekeken werd. De verandering in de BIC-waarden was bij de laatste modellen zo klein dat het toevoegen van extra kenmerken aan het model willekeuriger wordt. Bovenstaande tabel laat zien dat de eerste zeven kenmerken bij het validatiecohort hetzelfde zijn als bij het basiscohort (enkel kenmerk 4 en 5 zijn omgedraaid).
3.4 Stap 3: Kruisvalidaties
Na de stepwise analyse zijn er als derde stap kruisvalidaties uitgevoerd met de volgorde van kenmerken zoals beschreven in paragraaf 3.3. Tijdens deze analyse werd er eerst een leeg model geschat, om te onderzoeken wat de modelkwaliteit was zonder verklarende kenmerken. Daarna is er herhaaldelijk een nieuw model geschat waarbij telkens een extra kenmerk is toegevoegd op basis van de eerder vastgestelde volgorde. Uiteindelijk resulterend in het complete model met de elf kenmerken in het laatste model.
De kruisvalidaties zijn geëvalueerd met behulp van de fitmaten zoals beschreven in de bijlages 4.1.2 en 4.1.3 en worden weergegeven in tabel 3.4.1. Om de recall-, precision- en F1-waarde te kunnen berekenen zijn leerlingen ingedeeld in twee categorieën: geen vsv (0), en wel vsv (1). Dit is gedaan met een grenswaarde, zoals beschreven in bijlage 4.1.3. Bij de daadwerkelijke toepassing van het model zullen we niet gaan werken met een classificatie van 0 of 1, maar met de daadwerkelijke kansen per leerling om vsv’er te worden (waarde tussen 0 en 1). Deze fitmaten geven dus vooral een globaal beeld van de modelkwaliteit en dienen gebruikt te worden voor onderlinge modelvergelijkingen. Dit geldt niet voor de (relatieve) entropie en gemiddelde R2.
| Model | Entropie | Relatieve entropie1) | Gemiddelde R2 2) | Recall | Precision | F1 |
|---|---|---|---|---|---|---|
| intercept3) | 43 280 | . | . | . | . | . |
| 1 | 34 264 | 0,208 | 0,32 | 0,81 | 0,028 | 0,055 |
| 2 | 31 407 | 0,274 | 0,41 | 0,73 | 0,057 | 0,106 |
| 3 | 31 051 | 0,283 | 0,41 | 0,75 | 0,052 | 0,098 |
| 4 | 30 808 | 0,288 | 0,37 | 0,77 | 0,049 | 0,092 |
| 5 | 30 594 | 0,293 | 0,37 | 0,81 | 0,038 | 0,073 |
| 6 | 30 460 | 0,296 | 0,37 | 0,82 | 0,037 | 0,071 |
| 7 | 30 369 | 0,298 | 0,37 | 0,82 | 0,037 | 0,071 |
| 8 | 30 326 | 0,299 | 0,37 | 0,81 | 0,040 | 0,075 |
| 9 | 30 290 | 0,300 | 0,37 | 0,81 | 0,039 | 0,075 |
| 10 | 30 263 | 0,301 | 0,37 | 0,82 | 0,038 | 0,073 |
| 11 | 30 249 | 0,301 | 0,37 | 0,80 | 0,043 | 0,081 |
| 1) De relatieve entropie staat ook wel bekend als de McFadden (1974) pseudo-R2-waarde en kan daarbij ook vergeleken worden met de gemiddelde R2. 2) We geven de gemiddelde R2 weer, omdat deze per groep in de kruisvalidatie wordt berekend zoals beschreven in Bijlage ‘Fitmaten voor logistische regressie’. 3) Voor het intercept model worden geen fitmaten (excl. de entropie) weergegeven, omdat deze geen informatieve waarde hebben in de vergelijking van de modellen met kenmerken. | ||||||
In de tabel zien we dat de entropie-waarde afneemt, naarmate het model uitgebreider wordt. Dit betekent dat hoe uitgebreider het model, des te beter het model wordt in het schatten van de kans op vsv. De relatieve entropie geeft de relatieve verbetering ten opzichte van het lege model weer. De toename blijft oplopen, maar vlakt af rond het model met zeven kenmerken.
De recall-waarde ligt tussen de 0,73 en 0,82. Dit betekent dat het model de leerlingen die werkelijk vsv’er worden vaak als zodanig classificeert. De precision ligt echter tussen de 0,03 en 0,06 in, wat een relatief lage waarde is, maar die wel in lijn is met het lage aandeel vsv’ers in de populatie (0,8% op het vo, zie ook paragraaf 2.4). De precision laat zien dat de modellen met achtergrondkenmerken het een stuk beter doen dan een leeg model. Stel de achtergrondkenmerken worden niet meegenomen en iedereen zou als vsv’er geclassificeerd worden, dan zou de precision gelijk zijn aan het aandeel vsv’ers in de vo populatie, dus 0,008. Dan is een precision van 0,03 tot 0,06 weer een relatieve verbetering. De F1-waarde vat bovenstaande resultaten van de recall- en precision-waarde samen.
De gemiddelde McKelveyZavoina R2 over de vijf kruisvalidaties ligt tussen de 0,32 en 0,41, maar ligt voor de meeste modelvarianten dicht bij elkaar. Deze R2 variant moet met voorzichtigheid worden geïnterpreteerd en de grootte van het effect is daarbij ook context-afhankelijk. We gebruiken de R2 in de kruisvalidaties dan ook voornamelijk om modelvergelijkingen te maken. Daaraan zien we dat de modellen met twee en drie kenmerken de hoogste waarde hebben. Voor de overige modellen ligt de waarde wat lager. Omdat een model met twee of drie kenmerken wel erg beperkt is en weinig inzicht geeft in de achtergrondkenmerken die bijdragen aan het risico op vsv, gaat de voorkeur uit om naar de uitgebreidere varianten te kijken.
3.5 Conclusie modelselectie
Op basis van bovenstaande resultaten is een definitief voorkeursmodel voor het vo geselecteerd. Het is daarbij van belang om een model te selecteren op basis van de modelkwaliteit en stabiliteit. Daarnaast wil je een zo informatief mogelijk model, dat toch eenvoudig, transparant en goed uit te leggen blijft. Op basis van deze criteria is het model met zeven kenmerken gekozen. Ten eerste zien we in figuur 3.3.1 dat de BIC-waarde niet veel verder afneemt na zeven kenmerken. Ten tweede zien we dat de selectie van de eerste zeven kenmerken stabiel blijft tussen de twee onderzochte cohorten. Ook blijkt uit stap 3 dat de modelkwaliteit bij zeven kenmerken vergelijkbaar blijft met modellen die uitgebreider zijn. Het verder uitbreiden van het model heeft dan ook weinig toegevoegde waarde.4) De coëfficiënten en odds ratio’s behorende tot het model met zeven kenmerken worden weergegeven in bijlage 5.
Met behulp van de gegevens in figuur 3.5.1 kan een voorbeeld gegeven worden van de toepassing van de odds ratio’s voor een fictieve leerling. Deze leerling heeft bepaalde kenmerken, zoals een leeftijd van 19 jaar of ouder en relatief hoge welvaart. Elke categorie waarin een leerling valt, heeft een odds ratio ten opzichte van de referentiecategorie. Door vervolgens deze met elkaar te vermenigvuldigen, komen we uit op de odds op vsv van de betreffende leerling. Zie paragraaf 2.7 voor een uitgebreidere uitleg van odds en odds ratio’s. Volgens de figuur is de kans op vsv voor die leerling 1,307 keer zo groot als de kans op geen vsv. Bij deze kansverhouding hoort een geschatte kans op vsv van 0,567. De kans dat een leerling met deze combinatie van achtergrondkenmerken vsv’er wordt is dus 56,7%.
3.6 Stap 4: Uitbreiding met multilevel-component
Leerlingen zijn geclusterd binnen scholen en scholen zijn weer geclusterd binnen RMC-regio’s. Zoals eerder is opgemerkt in paragraaf 2.7 zou het kunnen dat twee jongeren die op dezelfde school zitten of binnen dezelfde regio naar school gaan relatief vaker allebei wel of allebei geen vsv’er worden dan twee jongeren op verschillende scholen of uit verschillende regio’s. Om te onderzoeken hoe sterk dit clustereffect is en of hier in de analyses rekening mee gehouden dient te worden, hebben we in stap 4 multilevel modellen geschat.
Allereerst is gekeken naar clustering op het hoogste niveau, te weten RMC-regio. In een model waarin alleen een random intercept op RMC-regioniveau is opgenomen was de Median Odds Ratio (MOR) 1,30 (95% betrouwbaarheidsinterval (BI): 1,23-1,41). Dat wil zeggen dat wanneer een leerling verhuist van een RMC-regio met een lagere odds op vsv naar een RMC-regio met een hogere odds op vsv, de mediane odds op vsv 1,3 keer zo groot zijn. Aangezien de MOR een odds ratio is, kan hij ook direct vergeleken worden met de andere odds ratio’s van de variabelen in het model. In verhouding is dit effect van RMC-regio dusdanig klein, dat wij hebben besloten hier in de modelontwikkeling geen rekening mee te houden. Aanvullend is wel nog onderzocht of deze MOR nog kleiner werd na het toevoegen van de zeven geselecteerde verklarende variabelen, wat inderdaad het geval was.
Vervolgens is de clustering binnen scholen onderzocht. In het model met alleen een random intercept op schoolniveau was de MOR 2,91 (95% BI:2,72-3,13). Het schooleffect is dus aanzienlijk groter dan het effect van RMC-regio, d.w.z. er is een veel sterkere clustering binnen scholen dan binnen RMC-regio’s. Vervolgens zijn aan het model met het random intercept op schoolniveau de zeven geselecteerde verklarende variabelen toegevoegd. Na toevoeging van deze variabelen was de MOR nog maar 1,46 (95% BI:1,40-1,52). De variabelen konden de clustering binnen de scholen dus al voor een groot deel verklaren. Verder hebben we de geschatte coëfficiënten van de verklarende variabelen vergeleken tussen het model met een random intercept op schoolniveau en het model zonder multilevel-component. Er waren geen duidelijke verschillen zichtbaar tussen deze geschatte coëfficiënten, wat betekent dat de geschatte kansen op vsv uit beide modellen in de praktijk dicht bij elkaar zouden liggen. Daarom is besloten dat in de modelontwikkeling geen rekening hoeft te worden gehouden met de clustering binnen scholen. De conclusie is dat een multilevel component niet nodig is voor het vo model.
Bij het validatiecohort vonden wij vergelijkbare resultaten. In het model met alleen een random intercept op het niveau van RMC-regio was de MOR 1,31 (95% BI:1,23-1,42). In het model met alleen een random intercept op schoolniveau was de MOR 2,96 (95% BI:2,77-3,19) en na toevoeging van de zeven verklarende variabelen nog maar 1,48 (95% BI:1,42-1,55).
Hoewel de gevonden clusteringseffecten klein zijn, zijn ze wel statistisch significant. Hierbij moet worden bedacht dat de onderzoekspopulatie een groot aantal waarnemingen bevat waardoor de kans op statistisch significante resultaten wordt vergroot.
3.7 Extra analyses
Tot slot zijn er twee aanvullende analyses uitgevoerd. Ten eerste hebben we, om de resultaten van het model te valideren, ook een vergelijkbare analyse uitgevoerd op basis van DUO-data. Zoals beschreven in de inleiding van dit rapport, hanteert DUO een andere definitie van zowel vsv als de populatie dan het CBS. We willen deze data daarom vooral gebruiken om te zien of een model op basis van DUO-data tot een vergelijkbare selectie van kenmerken komt als met CBS-data. Om de resultaten te valideren, is de stepwise procedure daarom opnieuw toegepast.
In tabel 3.7.1 worden de resultaten vergeleken. De stepwise procedure resulteert voor de DUO-data in een selectie van dertien kenmerken, in vergelijking met elf op basis van de CBS-data. Zoals in paragraaf 3.5 besproken is het model (op basis van de CBS-data) met zeven kenmerken ons voorkeursmodel. Deze zeven kenmerken komen ook naar voren in de analyses op basis van de DUO-data. Dit is een extra bevestiging dat deze zeven kenmerken belangrijk zijn om de kans op vsv te schatten.
| Volgorde | Kenmerken (CBS 2018/’19) | Kenmerken (DUO 2018/’19) |
|---|---|---|
| 1 | Leeftijd | Leeftijd |
| 2 | Onderwijssoort | Onderwijssoort |
| 3 | Psychosociale problemen | Ouderlijke structuur |
| 4 | Vertraging | Psychosociale problemen |
| 5 | Welvaart huishouden | Migratieachtergrond |
| 6 | Ouderlijke structuur | Verdacht van misdrijf |
| 7 | Verdacht van misdrijf | Vertraging |
| 8 | Geslacht | Problematische schulden in huishouden |
| 9 | Problematische schulden in huishouden | Geslacht |
| 10 | Hoogst behaalde opleidingsniveau moeder | Welvaart huishouden |
| 11 | Langdurige gezondheidsproblemen | Langdurige gezondheidsproblemen |
| 12 | Ouder(s) wanbetaler zorgverzekering | |
| 13 | Hoogst behaalde opleidingsniveau moeder | |
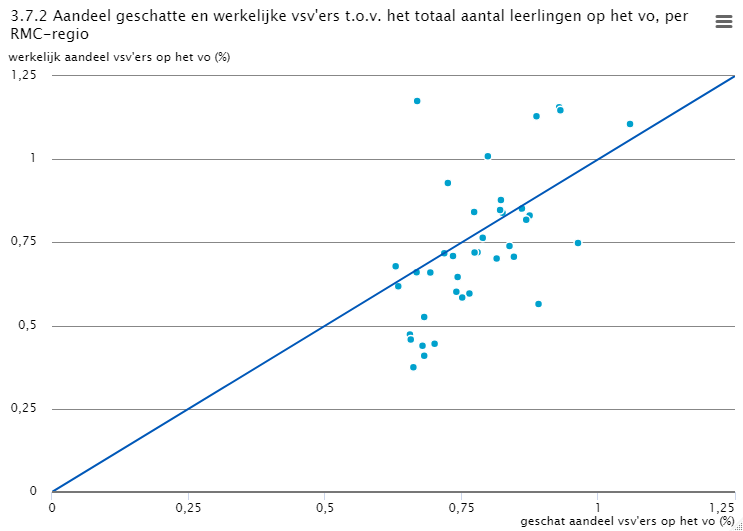
Ten tweede hebben we op basis van het eindmodel met zeven kenmerken voor de totale populatie op het vo een simpele aggregatie uitgevoerd van de geschatte kansen op vsv. Dit betekent dat de geschatte kansen van alle leerlingen in een bepaalde RMC-regio bij elkaar zijn opgeteld. Hiermee krijgen we al een eerste indicatie van de verschillen tussen het werkelijke en geschatte aantal vsv’ers en hoe dit tussen regio’s verschilt. In fase 2 van dit onderzoek zal deze aggregatie naar RMC-niveau uitvoerig onderzocht worden. Hierbij zullen ook verschillende beleidskeuzes door OCW gemaakt moeten worden.
Om een eerste indicatie te geven van de samenhang tussen het werkelijke en geschatte aantal vsv’ers per RMC-regio op het vo, hebben we de Pearson correlatiecoëfficiënt uitgerekend. Deze geeft een sterke samenhang aan tussen het werkelijke en geschatte aantal vsv’ers met \( \rho = 0,974 \). Dit betekent dat we op basis van het (in dit onderzoek) ontwikkelde model dus een goede schatting kunnen maken van de mate waarin regio’s te maken met vsv-problematiek. In onderstaande figuur staat deze samenhang visueel weergegeven. Omdat aantallen afhankelijk zijn van het aantal leerlingen op RMC-regio, hebben we in figuur 3.7.2 de aantallen uitgedrukt als percentage van het totaal aantal leerlingen per regio. Het totaal aantal leerlingen is gedefinieerd zoals in dit gehele rapport: leerlingen zonder startkwalificatie.