Verkenning alternatief verdeelmodel voor voortijdig schoolverlaten
Over deze publicatie
Ondanks de zorgvuldigheid waarmee dit rapport is samengesteld, is gebleken dat jeugdhulp niet correct meegenomen is bij de operationalisatie van psychosociale problemen. Tijdens het herstellen van deze fout is besloten om de operationalisatie verder te verbeteren door naar jeugdhulp tot 23 jaar te kijken in plaats van enkel tot 18 jaar. Dit heeft geresulteerd in betere modellen.
De juiste versie van dit rapport, met de nieuwe en verbeterde modellen, is te vinden via de volgende link: https://www.cbs.nl/nl-nl/longread/aanvullende-statistische-diensten/2023/verkenning-alternatief-verdeelmodel-voor-voortijdig-schoolverlaten-herziene-versie.
Het ministerie van Onderwijs, Cultuur en Wetenschap (OCW) wil het financiële verdeelmodel voor voortijdig schoolverlaten (vsv) herzien. Het Centraal Bureau voor de Statistiek (CBS) heeft op verzoek van het ministerie van OCW verkend of het mogelijk is om, op basis van kenmerken die in registraties bij het CBS aanwezig zijn, een indicator te ontwikkelen om de omvang van de vsv-problematiek per regio te schatten.
In het huidige rapport staat de vraag centraal of een model ontwikkeld kan worden om per leerling of student de kans op vsv te schatten. Daarbij wordt onderzocht welke combinatie van kenmerken het beste hiervoor gebruikt kan worden. Hierbij zijn aparte modellen ontwikkeld voor het voorgezet onderwijs en voor het middelbaar beroepsonderwijs. De uitkomsten worden in dit rapport beschreven, net als de methode en data waarmee de modellen zijn berekend.
Erratum
Ondanks de zorgvuldigheid waarmee dit rapport is samengesteld, is gebleken dat jeugdhulp niet correct meegenomen is bij de operationalisatie van psychosociale problemen. Tijdens het herstellen van deze fout is besloten om de operationalisatie verder te verbeteren door naar jeugdhulp tot 23 jaar te kijken in plaats van enkel tot 18 jaar. Dit heeft geresulteerd in betere modellen.
De juiste versie van dit rapport, met de nieuwe en verbeterde modellen, is te vinden via de volgende link: https://www.cbs.nl/nl-nl/longread/aanvullende-statistische-diensten/2023/verkenning-alternatief-verdeelmodel-voor-voortijdig-schoolverlaten
1. Inleiding
Het doel van de herziening is om tot een verdeling te komen waarmee RMC-regio’s zo effectief en transparant mogelijk potentieel vsv kunnen voorkomen en bestrijden. Hierbij neemt het ministerie van OCW aan dat probleemgerichte financiering het meest effectief is: het geld moet worden verdeeld op basis van waar de uitdagingen het grootst zijn. Het ministerie van OCW beoogt hiermee tot een verdeling van de vsv-middelen te komen die recht doet aan de opgave waar een RMC-regio voor staat. Om het vsv-budget over RMC-regio’s te verdelen is het ministerie van OCW daarom op zoek naar een nieuwe indicator om de omvang van de vsv-problematiek per regio te schatten. Het is daarbij belangrijk dat de nieuwe indicator geen perverse prikkels kent en daarnaast transparant en duidelijk is, zodat regio’s begrijpen hoe het geld wordt verdeeld.
Om tot een nieuwe verdeelsystematiek te komen, heeft het ministerie van OCW het Centraal Bureau voor de Statistiek (CBS) gevraagd om, op basis van kenmerken die in registraties bij het CBS aanwezig zijn, een indicator te ontwikkelen waarmee de kans wordt berekend dat leerlingen en studenten voortijdig schoolverlater (vsv’er) worden. Om tot een gedragen en gedegen model te komen, heeft het ministerie van OCW een begeleidingscommissie (zie bijlage 1) ingesteld die gedurende het onderzoek heeft meegedacht over de aanpak, resultaten en implicaties hiervan.
Uit eerder onderzoek van het CBS bleek dat de aanwezigheid van vsv en de kenmerken van jongeren verschilden tussen het voortgezet onderwijs (vo) en het middelbaar beroepsonderwijs (mbo). Daarnaast laten de resultaten van dat onderzoek zien dat de kans op vsv met andere kenmerken samenhangt op het vo dan op het mbo. Bij de ontwikkeling van een nieuwe verdeelsystematiek is er daarom voor gekozen om aparte modellen te schatten voor het vo en het mbo.
Het huidige rapport betreft de resultaten uit de eerste fase van het onderzoekstraject. Hierin staat de ontwikkeling van een model centraal waarmee op individueel niveau de kans op vsv zal worden geschat. In de tweede fase zal een methode worden uitgewerkt om deze kansen te aggregeren naar een score per RMC-regio en zullen de gevolgen van de nieuwe verdeelsystematiek in kaart worden gebracht.
Dit rapport bestaat uit de volgende onderdelen: hoofdstuk 2 gaat uitgebreid in op de aanpak van het onderzoek. In hoofdstuk 3 wordt de ontwikkeling van een model voor het vo besproken. Hoofdstuk 4 gaat in op de ontwikkeling van een model voor het mbo. Hierop volgt een conclusie en een vooruitblik in hoofdstuk 5.
2. Data en methoden
2.1 Inleiding
In dit hoofdstuk bespreken we de data en methoden op basis waarvan een model is ontwikkeld om het risico op voortijdig schoolverlaten (vsv) in het vo en het mbo zo goed mogelijk te schatten. Dit hoofdstuk is als volgt opgezet: in paragraaf 2.2 bespreken we de gebruikte databronnen. In paragraaf 2.3 gaan we in op de populatie waarvoor de kans op vsv is geschat. Vervolgens komt in paragraaf 2.4 de operationalisering van vsv aan bod. In paragraaf 2.5 worden de kenmerken besproken die zijn meegenomen in het onderzoek. De imputatie van het opleidingsniveau van de ouders komt aan bod in paragraaf 2.6. In paragraaf 2.7 gaan we tenslotte in op de gebruikte analysemethode. Deze methode bestaat uit een aantal stappen die één voor één zullen worden uitgelegd.
2.2 Gebruikte databronnen
In dit onderzoek is gebruik gemaakt van gegevens uit het Stelsel van Sociaal-Statistische Bestanden (SSB) van het CBS. Het SSB bevat een groot aantal microdatabestanden met informatie uit administratieve overheidsregisters over personen en huishoudens. Het CBS ontvangt deze informatie vanwege zijn wettelijke taak. De data bevatten geen namen, geen adressen en geen burgerservicenummers. Om gegevens uit verschillende bronnen aan elkaar te verbinden worden gepseudonimiseerde koppelsleutels gebruikt die buiten het SSB geen betekenis hebben. Individuele personen zijn hierdoor niet direct te identificeren. Zie bijlage 2 voor meer informatie over de bestanden uit het SSB die zijn gebruikt.
2.3 Populatie
De groep leerlingen en studenten voor wie de kans op vsv geschat zal worden noemen we de populatie. De populatie in dit onderzoek bestaat uit jongeren die op 1 oktober 2018 staan ingeschreven in het vo, mbo of voortgezet algemeen volwassenenonderwijs (vavo) (cohort 2018/’19). Er is gekozen voor dit cohort omdat dit het meeste recente cohort voor de start van de coronacrisis is. Tijdens de coronacrisis waren er afwijkende patronen in de ontwikkeling van vsv te zien. Het is niet wenselijk om dit mee te nemen bij de ontwikkeling van het model, omdat dit mogelijk tot een vertekend beeld kan leiden.
Daarnaast bevat de populatie enkel jongeren die op 1 oktober 2018 (het startmoment, t0) 12 tot 26 jaar waren. De geplande verhoging van de vsv-leeftijd is meegenomen in de ontwikkeling van de modellen. Daarnaast wordt, zoals al benoemd werd in de inleiding, onderscheid gemaakt tussen een vo- en mbo-populatie. Vavo-leerlingen zijn een relatief kleine groep waardoor voor hen geen apart model kan worden samengesteld. Deze leerlingen worden daarom tot de vo-populatie gerekend.
Om te onderzoeken welke jongeren een grotere kans hebben om vsv’er te worden moet de populatie alleen bestaan uit personen die op het startmoment (t0) nog kans hebben om vsv’er te worden. Dit betekent dat we de gebruikelijke startpopulatie om het aandeel nieuwe vsv’ers te meten nader moeten afbakenen tot jongeren die op 1 oktober 2018 nog géén startkwalificatie hadden. Jongeren die op 1 oktober 2018 al wel een startkwalificatie hadden kunnen namelijk per definitie geen vsv’er meer worden op 1 oktober 2019 (t1). Een startkwalificatie is een diploma op ten minste havo-, vwo- of mbo 2-niveau. Dit wordt door het CBS gemeten via het zogenaamde opleidingsniveaubestand (zie bijlage 2).
In het onderzoek is bovenstaande populatie ook vergeleken met een eerder cohort (2017/’18) om het model te valideren, dat wil zeggen dat we onderzoeken of de resultaten in het ontwikkelde model robuust zijn. Dit cohort noemen we in het rapport het validatiecohort.
In dit onderzoek volgen we de methode van het CBS om vsv in kaart te brengen. In een aanvullende analyse om het model te valideren, is de modelselectie ook toegepast op een dataset van de Dienst Uitvoering Onderwijs (DUO) en onderzocht of dit leidt tot een vergelijkbare selectie en volgorde van kenmerken. Zowel het CBS als DUO sluiten personen uit die op t0 (1 oktober 2018) staan ingeschreven in het praktijkonderwijs, de Engelse Stroom, het Internationaal Baccalaureaat, de volwasseneneducatie of het speciaal onderwijs. Daarnaast sluiten ze beiden personen uit die op t1 (1 oktober 2019) een vrijstelling van de leerplicht hebben. Er zijn echter ook een aantal verschillen tussen de methodes van het CBS en DUO.
Een belangrijk verschil in beide methodes is dat het CBS de Basisregistratie Personen (BRP) gebruikt om af te bakenen welke jongeren op t0 en t1 in Nederland wonen. DUO gebruikt hiervoor de Registratie Onderwijsdeelnemers (ROD, voorheen bekend als BRON). In de data van DUO komen in het vo hierdoor enkele honderden leerlingen voor die niet in de BRP staan ingeschreven. Voor deze leerlingen kan geen informatie uit andere registers in het SSB worden aangekoppeld. Hierdoor hebben wij de betreffende leerlingen uiteindelijk niet in de vergelijkende analyse meegenomen. Een ander verschil is dat er in de dataset van DUO nog sprake is van een leeftijdgrens van 22 jaar op t0. Hierbij kan dus geen rekening gehouden worden met de verhoging van de vsv-leeftijd. Ook zijn eerstejaars nieuwkomers niet meegenomen in de populatie van DUO. Tevens worden jongeren die op t1 zijn uitgestroomd naar bepaalde onderwijssoorten, zoals speciaal onderwijs of praktijkonderwijs niet meegenomen in de CBS-populatie maar wel in de DUO-populatie. Tot slot neemt DUO bij het bepalen van een startkwalificatie ook diploma’s mee van niet-bekostigde instellingen. Het CBS neemt dit enkel indirect en slechts gedeeltelijk mee via het opleidingsniveaubestand (zie bijlage 2).
2.4 Operationalisering vsv
Vsv’ers zijn jongeren tot 27 jaar die op 1 oktober 2019 (t1) het onderwijs hebben verlaten vanuit het vo, mbo of vavo zonder een startkwalificatie. Het zijn dus jongeren die op 1 oktober 2018 (t0) ingeschreven staan in het bekostigd vo, mbo of vavo en op 1 oktober 2019 (t1) niet meer ingeschreven staan in het onderwijs, geen startkwalificatie hebben én jonger zijn dan 27 jaar.
De precieze definitie van vsv verschilt tussen het CBS en DUO. DUO rekent de volgende jongeren niet tot vsv’ers:
- jongeren die doorstromen naar niet-bekostigd onderwijs;
- jongeren die een opleiding gaan volgen bij politie of defensie;
- jongeren die tussen 1 oktober en 31 december in jaar t1 alsnog een startkwalificatie behalen;
- jongeren met een mbo-entreediploma die 12 uur of meer werken op 1 oktober.
Zoals ook te zien is in tabel 2.4.1 is het percentage vsv daarom lager in de DUO-populatie in vergelijking met de CBS-populatie. Daarnaast kan, zoals in de vorige paragraaf al beschreven werd, in de DUO-data geen rekening gehouden worden met de verhoging van de vsv-leeftijd. In deze data wordt nog de oude grens gebruikt van 23 jaar.
Uit onderstaande tabel komt ook duidelijk naar voren dat vsv minder vaak voorkomt onder scholieren op het vo dan onder mbo-studenten. Bij het ontwikkelen van een model zal de betrouwbaarheid toenemen wanneer het te verklaren fenomeen vaker voorkomt. De verwachting is daarom ook dat de kans op vsv voor het mbo nauwkeuriger te schatten is dan de kans op vsv voor het vo.
| vo | mbo | |||
|---|---|---|---|---|
| aantal | % | aantal | % | |
| CBS-data | ||||
| Wel vsv'er | 7 430 | 0,8 | 27 820 | 7,9 |
| Geen vsv'er | 921 400 | 99,2 | 326 460 | 92,1 |
| Totaal | 928 830 | 100 | 354 280 | 100 |
| DUO-data | ||||
| Wel vsv'er | 4 960 | 0,5 | 21 720 | 6,4 |
| Geen vsv'er | 923 520 | 99,5 | 515 020 | 93,6 |
| Totaal | 928 480 | 100 | 336 740 | 100 |
2.5 Onderzochte kenmerken
Samen met de begeleidingscommissie hebben het CBS en het ministerie van OCW eerst een lijst met mogelijke verklarende variabelen van vsv opgesteld. Deze lijst is uitgebreid met kenmerken die in twee eerdere onderzoeken van het CBS naar vsv van belang bleken te zijn. Ook zijn op basis van de uitkomsten van ander CBS-onderzoek naar verdeelmodellen nog aanvullende kenmerken toegevoegd.
Een aantal van de kenmerken in deze lijst is op basis van de registraties die het CBS (op dit moment) tot zijn beschikking heeft niet in kaart te brengen. Dit kan zijn omdat gegevens (nog) niet beschikbaar zijn bij het CBS of omdat sommige gegevens niet integraal worden gemeten en daardoor niet voor alle leerlingen of studenten beschikbaar zijn. Daarnaast waren een aantal zeer vergelijkbare suggesties opgenomen (zie volgende alinea’s bij de bespreking van de kenmerken). In overleg met inhoudelijke experts bij het CBS is voor het best passende kenmerk gekozen.
In deze paragraaf worden de kenmerken beschreven die in het onderzoek zijn meegenomen als mogelijke verklarende variabelen van vsv. Eerst zullen de kenmerken worden benoemd die voor zowel het vo als het mbo in kaart gebracht kunnen worden. Vervolgens zullen nog enkele onderwijsgerelateerde kenmerken worden benoemd die specifiek op één van beide onderwijssoorten (vo of mbo) van toepassing zijn. In sommige gevallen zijn dezelfde kenmerken onderzocht voor zowel het vo als het mbo, maar wel met verschillende operationaliseringen. Een uitgebreid overzicht van de operationalisering van de kenmerken is te vinden in bijlage 3.
Sociaal-demografische kenmerken
Twee eerdere onderzoeken van het CBS in 2020 en 2021 naar de relatie tussen multiproblematiek en vsv lieten zien dat geslacht, leeftijd en migratieachtergrond gerelateerd zijn aan de kans op vsv. Daarnaast bleken jongeren die niet meer bij beide juridische ouders wonen een hogere kans te hebben op vsv. Dit gold ook voor jongeren van wie hun juridische ouder niet bekend is in de registers van het CBS, bijvoorbeeld omdat de ouder in het buitenland woont. Ook waren de hoogte van het huishoudinkomen en het hoogst behaalde opleidingsniveau van de vader en moeder van belang. Het opleidingsniveau is niet voor alle personen bekend. Daarom zijn ontbrekende waarden geïmputeerd (zie paragraaf 2.6 voor meer informatie).
Deze sociaal-demografische kenmerken zijn ook meegenomen in eerder CBS-onderzoek naar de ontwikkeling van verdeelmodellen voor onderwijsachterstanden. In het uiteindelijke model voor de Onderwijs Achterstanden Indicator in het primair onderwijs zijn de volgende kenmerken opgenomen: opleidingsniveau van moeder en vader, herkomstland van de jongere en verblijfsduur van de moeder in Nederland.
De begeleidingscommissie onderstreepte het belang van het toevoegen van deze sociaal-demografische kenmerken, met name de leeftijd en de migratieachtergrond en het aantal verblijfsjaren in Nederland van de jongere. Ook de aanwezigheid van een laag huishoudinkomen, armoede en bijstand en de sociaaleconomische status werden aangedragen. Het CBS heeft dit op advies van een inhoudelijke expert samengevoegd tot één kenmerk, te weten ‘welvaart’. Hierbij wordt rekening gehouden met de hoogte van het huishoudinkomen én van het vermogen. Tot slot adviseerde de commissie om het hebben van een bijbaan op te nemen in de lijst van mogelijke verklarende variabelen van vsv. Dit is geoperationaliseerd door middel van het aantal uren dat een jongere per week werkt.
De volgende sociaal-demografische kenmerken zijn uiteindelijk opgenomen in de lijst:
- Geslacht van de jongere
- Leeftijd van de jongere
- Herkomstland (van jongere en ouders)
- Migratieachtergrond (van jongere en ouders)
- Verblijfsduur in Nederland (van jongere en ouders)
- Ouderlijke structuur
- Ouders niet bekend
- Hoogst behaalde opleiding van de ouders
- Welvaart van het huishouden
- Huishoudinkomen onder de lage inkomensgrens
- Aantal gewerkte uren door de jongere
Aanwezigheid van problemen
Problemen van jongeren en hun ouders hangen sterk samen met de kans dat een jongere een vsv'er wordt. Het CBS heeft in 2020 een literatuurstudie uitgevoerd naar de aanwezigheid van (multi)problematiek bij de jongere en de relatie met vsv. Vervolgens heeft het CBS in 2021 onderzocht welke van deze problemen het sterkst samen hangen met vsv. Deze studie liet zien dat psychosociale problemen van de jongere en van de moeder sterk samenhangen met de kans op vsv. Hierbij is gekeken naar het gebruik van jeugdhulp en/of GGZ. Daarnaast bleken gezondheidsproblemen de kans op vsv te vergroten. In dit huidige onderzoek maken we, op advies van de inhoudelijke experts van het CBS, onderscheid tussen langdurige en acute gezondheidsproblemen. Verder was te zien dat jongeren die verdacht zijn geweest van een delict een verhoogde kans hebben op vsv. Registratie door de politie als verdachte van een misdrijf is daarom toegevoegd aan de lijst. Ook schulden in het huishouden leiden tot een hogere kans op vsv. Dit kan op verschillende manieren gemeten worden. In onze studie is, in overleg met een inhoudelijk expert, gekozen om zowel een specifieke variabele (wanbetaler van de zorgverzekering) als een complexere variabele (problematische schulden, waarbij is gekeken naar een breder scala aan mogelijke schulden) op te nemen in de lijst. Tot slot droeg de begeleidingscommissie de suggestie aan om te kijken naar ongeoorloofd verzuim van de jongere. Er zijn op dit moment enkel registraties beschikbaar rondom de overtreding van de leerplichtwet bij Bureau Halt.
Samenvattend zijn de volgende probleemgerelateerde kenmerken uiteindelijk toegevoegd aan de lijst:
- Psychosociale problemen (bij jongere en moeder)
- Langdurige gezondheidsproblemen bij de jongere
- Acute gezondheidsproblemen bij de jongere
- Jongere is verdachte van een delict
- Ouders zijn wanbetaler ZVW-premie
- Problematische schulden
- Ongeoorloofd verzuim door de jongere
Omgevingskenmerken
De omgeving waarin de jongere woont kan ook invloed hebben op de kans dat een jongere vsv'er wordt. Op advies van de begeleidingscommissie zijn daarom de volgende kenmerken toegevoegd aan de lijst. Zo kan een hoge jeugdwerkloosheid of veel armoede in de buurt een jongere aanmoedigen om wel een diploma te behalen en zo zijn of haar kansen op de arbeidsmarkt te vergroten. Aan de andere kant kan het ook zo zijn dat de jongere hierdoor ontmoedigd wordt en daarom besluit te stoppen met de opleiding. Een sterk stedelijke omgeving kan extra kansen bieden voor een jongere, maar ook mogelijk voor afleiding zorgen. In welke richting deze effecten lopen zal bij de ontwikkeling van het model naar voren komen.
Kortom, de volgende omgevingskenmerken zijn opgenomen in de lijst met te onderzoeken variabelen:
- Stedelijkheid van de buurt
- Jeugdwerkloosheid in de gemeente
- Lage welvaart in de buurt
Onderwijsgerelateerde kenmerken
Een aantal kenmerken kan alleen onderzocht worden voor één van de onderzoekspopulaties. Voor het vo zijn twee specifieke kenmerken voorgesteld. Ten eerste laat het CBS-onderzoek uit 2020 duidelijke verschillen zien in het aandeel vsv’ers naar onderwijssoort. Dit aandeel lag het hoogst bij leerlingen uit leerjaar 3-4 van het vmbo. De begeleidingscommissie gaf hierbij aan dat het ook waardevol is om specifiek de leerwegen binnen het vmbo te onderscheiden. Ook is het van belang om onderscheid te maken tussen jongeren die het reguliere voortgezet onderwijs volgen en degenen die vavo volgen. De laatste categorie kent een hoger aandeel vsv’ers. Ten tweede is voor het vo op basis van het leerjaar1) en de leeftijd gekeken of jongeren vertraging hebben opgelopen in hun onderwijsloopbaan.
Voor het mbo zijn vier extra variabelen meegenomen. Ten eerste bleek uit eerder onderzoek dat er grote verschillen waren in het aandeel vsv’ers tussen niveaus binnen het mbo. Het aandeel was veruit het hoogst bij de entreeopleiding. Ten tweede waren er ook verschillen te zien in de leerweg: zo lag het aandeel vsv’ers veel hoger bij studenten die de beroepsbegeleidende leerweg (BBL) volgden in vergelijking met studenten die de beroepsopleidende leerweg (BOL) volgden. De begeleidingscommissie stelde daarnaast voor om naar de studierichting van de gevolgde opleiding te kijken en het niveau van de vooropleiding van de student.
Samengevat zijn de volgende onderwijsgerelateerde variabelen opgenomen:
Voor het vo:
- Combinatie onderwijssoort en leerjaar
- Vertraging
Voor het mbo:
- Niveau
- Leerweg
- Studierichting (ISCED-indeling)
- Hoogst behaalde opleiding van de student
2.6 Imputatie opleidingsniveau van de ouders
De meeste kenmerken die in dit onderzoek worden gebruikt zijn bekend voor (bijna) alle jongeren in de populatie. Echter, de kenmerken opleidingsniveau van de moeder en de vader ontbreken voor een substantieel deel van de populatie. De opleidingsgegevens zijn afkomstig uit centrale opleidingsregistraties die in Nederland tussen de jaren 1980 en 2010 beschikbaar zijn gekomen, aangevuld met enquêtegegevens op steekproefbasis. Ontbrekende waarden komen daarom met name voor bij oudere mensen en mensen die hun opleiding in het buitenland hebben gevolgd. Eerder is bij de ontwikkeling van een indicator voor onderwijsachterstanden in het primair onderwijs door het CBS in 2016 een imputatiemethode ontwikkeld voor het opleidingsniveau van de ouders. Bij deze imputatiemethode worden de ontbrekende opleidingsniveaus vervangen door geschatte waarden, afkomstig uit een verdeling van mogelijke opleidingsniveaus. Bij het bepalen van de te imputeren waarden wordt rekening gehouden met een aantal hulpkenmerken die wel altijd bekend zijn. Dezelfde imputatiemethode is in 2021 ook toegepast op leerlingen in het vo.
Voor details over de gebruikte imputatiemethode, inclusief een test van de methode in een simulatiestudie, verwijzen we naar dit rapport. De methode is in het huidige onderzoek op dezelfde manier toegepast als eerder, met alleen enkele verschillen in de keuze van hulpkenmerken die worden meegenomen bij het imputeren:
- In het oorspronkelijke onderzoek werd de Cito-eindtoetsscore van een leerling gebruikt als hulpkenmerk bij het imputeren, omdat dit de doelvariabele was van de analyse uit dat onderzoek. Hier is in plaats daarvan het vsv-kenmerk gebruikt.
- Voor het hulpkenmerk herkomstland van vader en moeder is hier gebruikgemaakt van de nieuwe standaardindeling van het CBS.
- Voor het hulpkenmerk leeftijd van vader en moeder is een andere indeling in categorieën gebruikt. Er is 5 jaar opgeteld bij de grenzen tussen de categorieën om beter aan te sluiten bij de leeftijdsverdeling in onze doelpopulaties: ouders van jongeren in het vo en mbo zijn gemiddeld ouder dan ouders van leerlingen in het primair onderwijs.
De geïmputeerde opleidingsniveaus zijn willekeurige trekkingen uit een verdeling van mogelijke waarden. Om bij het schatten van modellen rekening te houden met de extra onzekerheid in de geïmputeerde waarden kan gebruik worden gemaakt van multipele imputatie (Rubin, 1987). Hierbij worden alle ontbrekende waarden meerdere keren geïmputeerd en wordt elk model meerdere keren geschat. Multipele imputatie maakt het uitvoeren van de stepwise aanpak die hieronder in paragraaf 2.7 wordt beschreven wel complexer.
Aangezien in dit onderzoek imputatie alleen speelt bij het opleidingsniveau van de ouders, en niet op voorhand duidelijk is of een van deze kenmerken als relevant naar voren zal komen, hebben we ervoor gekozen om in eerste instantie de hele aanpak te doorlopen voor één imputatieronde. Verder herhalen we de analyse voor één andere imputatieronde, ter controle dat de conclusies hierdoor niet veranderen. Als uit deze controle zou blijken dat de eerste imputatieronde stabiel is én het opleidingsniveau van de vader en/of moeder belangrijk is in het modelleren van vsv, houden we het bij de eerste imputatieronde. Als deze niet stabiel blijkt, zal multipele imputatie toegepast worden.
2.7 Opzet analyse
Aanpak
Het doel van dit onderzoek is om, voor zowel het vo als het mbo, een logistisch regressiemodel te ontwikkelen waarmee op individueel niveau de kans op vsv kan worden geschat. Gezien het grote aantal achtergrondkenmerken dat onderzocht moet worden en gezien de grootte van de beschikbare dataset, is ervoor gekozen om de analyses voor vo en mbo op te delen in verschillende stappen, zoals weergegeven in figuur 2.7.1. In dit hoofdstuk zullen deze stappen in detail besproken worden en zal de gebruikte analysemethode, logistische regressie, kort worden toegelicht.
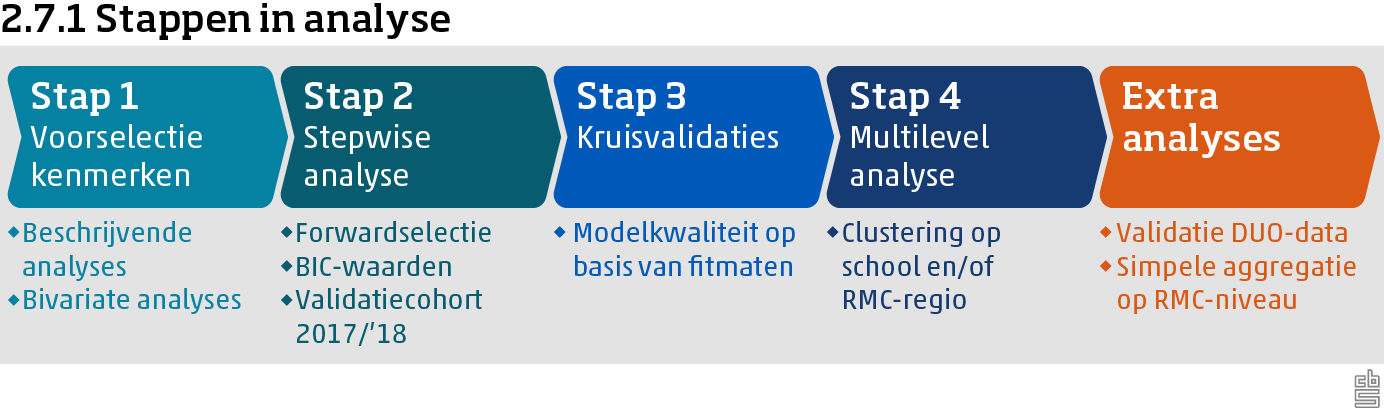
Gedurende deze stappen zullen de volgende onderzoeksvragen beantwoord worden:
- Welke combinatie van kenmerken uit paragraaf 2.5 kan het beste worden gebruikt om met een logistisch regressiemodel de kans op vsv te schatten (stap 1 en 2)?
- Hoe goed is dit model met de beste combinatie van kenmerken in staat om de kans op vsv voor individuele leerlingen en studenten te schatten (stap 3)?
- In hoeverre is het nuttig om in dit model rekening te houden met clustering per school of RMC-regio via een multilevel-component (stap 4)?
- In hoeverre kan het model gevalideerd worden met behulp van het DUO-cohort (extra analyse)?
- Hoe ziet een eerste beeld van een simpele aggregatie van de geschatte kansen op vsv op RMC-regio niveau eruit (extra analyse)?
Voor de ontwikkeling van de modellen gebruiken we data van leerlingen en studenten uit het cohort 2018/’19. Daarnaast worden data van leerlingen en studenten uit het cohort 2017/’18 gebruikt om bepaalde keuzes in de modelselectie te valideren. Voor alle analyses in dit rapport geldt dat zij worden uitgevoerd op de data van het cohort 2018/’19, tenzij anders aangegeven.
Logistische regressieanalyse
Met een regressieanalyse kan de samenhang tussen een afhankelijke variabele (vsv) en onafhankelijke variabelen (de opgestelde lijst met achtergrondkenmerken) onderzocht worden. Of een jongere wel of geen vsv’er wordt is een zogenaamde ‘dichotome’ uitkomst (de uitkomst kan óf de waarde 0 óf de waarde 1 aannemen). Om dichotome uitkomsten te schatten wordt vaak gebruik gemaakt van logistische regressieanalyse. Met deze techniek kan de samenhang tussen achtergrondkenmerken en een dichotome uitkomst berekend worden door te werken met een kansverhouding (de ‘odds’). In de huidige analyse is de odds gelijk aan de kans dat een persoon wel vsv’er wordt op t1 gedeeld door de kans dat de persoon geen vsv’er wordt op t1. Een odds van één geeft aan dat de kans om vsv’er te worden even groot is als de kans om dit niet te worden (dat wil zeggen: beide kansen zijn gelijk aan 0,5). Een odds boven de één geeft aan dat de kans om vsv’er te worden groter is, terwijl een odds tussen nul en één het omgekeerde betekent.
Vervolgens kan binnen de analyse gekeken worden welke achtergrondkenmerken samenhangen met de odds op vsv. Dat kan gedaan worden met behulp van de ‘odds ratio’ (OR). Alle achtergrondkenmerken in onze analyse zijn categoriale variabelen, wat betekent dat ze ingedeeld zijn in categorieën (zie bijlage 3 voor de operationalisering van alle kenmerken). Het kenmerk geslacht bestaat bijvoorbeeld uit de categorieën man en vrouw. Voor elk achtergrondkenmerk wordt één categorie de referentiecategorie (bijvoorbeeld man). Vervolgens wordt van elke andere categorie gekeken wat de odds op vsv is ten opzichte van de odds van deze referentiegroep. Dit is de odds ratio. Een odds ratio van 1,5 wil in dit geval dan zeggen dat de odds op vsv voor vrouwen 1,5 keer zo hoog is als voor mannen, gegeven dat alle andere kenmerken in het model hetzelfde zijn. Voor een uitgebreidere beschrijving van logistische regressie, zie bijlage 4.1. In de volgende paragrafen bespreken we de stappen zoals weergegeven in figuur 2.7.1.
Stap 1: Voorselectie kenmerken
Om te onderzoeken welke combinatie van achtergrondkenmerken de kans op vsv zo goed mogelijk kan schatten, is als eerste de samenhang tussen de kans op vsv en elk van de voorgestelde kenmerken afzonderlijk bekeken. Hiertoe berekenen we voor elk achtergrondkenmerk een kruistabel met het aantal jongeren dat wel of niet vsv’er is geworden op t1. Daarnaast zijn er eenvoudige (bivariate) logistische regressies uitgevoerd om met behulp van odds ratio’s vast te stellen of er een mogelijke samenhang is tussen het kenmerk en vsv. Bovendien wordt de mate van samenhang tussen het achtergrondkenmerk en vsv geëvalueerd met Cramérs V.2) Cramérs V ligt altijd tussen 0 en 1, waarbij 0 wijst op afwezigheid van samenhang en 1 op perfecte samenhang tussen het achtergrondkenmerk en vsv.
De resultaten van stap 1 worden gebruikt om een definitieve selectie te maken van achtergrondkenmerken die meegenomen worden in het verdere traject en om de categorieën van deze kenmerken definitief af te bakenen. Kenmerken die niet of nauwelijks samen lijken te hangen met vsv, of waarbij de gevonden odds ratio’s vanuit inhoudelijk oogpunt niet kunnen worden verklaard, zullen in deze stap afvallen.
Bij het kiezen van een model om de kans op vsv te schatten streven we enerzijds naar een model dat zo goed mogelijk past bij de beschikbare data. Anderzijds is de wens vanuit het ministerie van OCW om het model eenvoudig en transparant te houden. Naarmate de complexiteit van het model groter wordt, neemt namelijk ook het risico op overfitting toe: het geschatte model past dan met name goed bij de populatie van jongeren waarop het model is geschat, maar mogelijk minder goed bij andere populaties van jongeren, bijvoorbeeld van een jaar eerder of later. Het model zou dan minder geschikt zijn voor gebruik in een verdeelmodel over een langere periode. Om te evalueren hoe goed een model past bij de data, rekening houdend met de complexiteit van het model, kijken we in de volgende stappen naar een aantal verschillende fitmaten (zie bijlage 4.1.2) en valideren we de resultaten op basis van het validatiecohort en het DUO-cohort.
Stap 2: Stepwise analyse
Met de overgebleven kenmerken wordt een stepwise analyse uitgevoerd voor een verdere selectie van kenmerken. Hierbij wordt via een forward search gezocht naar het best passende model:
- Begin met een leeg logistisch regressiemodel (alleen een constante term).
- Bouw stap voor stap een groter model op door steeds één kenmerk toe te voegen dat leidt tot de grootste verbetering in het Bayesiaanse Informatie Criterium (BIC) (zie voor meer informatie over de BIC, de bijlage 4.1.2).
- Stop zodra de BIC-waarde niet meer verbetert door nog een kenmerk toe te voegen.
Deze procedure leidt tot een bepaalde volgorde voor de achtergrondkenmerken, waarbij de kenmerken die het belangrijkste zijn om de kans op vsv te schatten als eerste worden toegevoegd.
Naast de BIC berekenen we voor elk model uit de forward search ook de pseudo-R2-waarde (\( R^{2}_{MZ} \)) als evaluatiemaat (zie bijlage 4.1.2). De \( R^{2}_{MZ} \) geeft een indicatie welke fractie van de totale variantie in vsv wordt verklaard door de achtergrondkenmerken in het model.
Verder voeren we ter vergelijking ook een backward search uit:
- Begin met een volledig logistisch regressiemodel (alle beschikbare kenmerken opgenomen).
- Pel het model stap voor stap verder af door steeds één kenmerk weg te laten dat leidt tot de grootste verbetering qua BIC.
- Stop zodra de BIC niet meer verbetert door nog een kenmerk weg te laten.
Tot slot is er ook nog een combinatie van de forward en backward search gedaan, waarbij toegevoegde kenmerken later weer kunnen worden weggelaten en vice versa. Ter vergelijking worden dezelfde stepwise analyses ook uitgevoerd op het validatiecohort, om te zien in hoeverre de gevonden volgorde van kenmerken voor beide cohorten overeenkomt.
Stap 3: Kruisvalidaties
Op basis van de volgorde van achtergrondkenmerken die gevonden is in stap 2 voeren we een kruisvalidatie uit. De jongeren in de populatie worden verdeeld in vijf willekeurige, even grote groepen. Voor elke groep doen we het volgende:
- Gebruikmakend van de data van alle jongeren die niet behoren tot de huidige deelverzameling, schat alle logistische regressiemodellen waarin de eerste \( q \) achtergrondkenmerken uit de volgorde zijn opgenomen, waarbij \( q \) loopt van 0 tot en met het totale aantal achtergrondkenmerken dat in stap 2 in volgorde is gezet. (Hierbij komt \( q = 0 \) overeen met het ‘lege’ model dat alleen een constante term bevat.)
- Pas elk van de geschatte modellen toe om de kans op vsv te schatten voor de jongeren in de huidige deelverzameling.
Per model geeft deze stap voor alle jongeren in de populatie een geschatte kans op vsv. Dankzij de kruisvalidatie zijn de geschatte kansen voor elke jongere afkomstig uit modellen die zijn geschat zonder die jongere mee te nemen. Op deze manier wordt het risico op overfitting verminderd. Met deze geschatte kansen berekenen we vervolgens de evaluatiematen uit bijlage 4.1.2: de relatieve entropie \( \Delta(M) \) en \( R^{2}_{MZ} \) gemiddeld over de vijf ronden van de kruisvalidatie. Ook berekenen we de recall, precision en F1-score; zie bijlage 4.1.3. De recall geeft aan hoeveel procent van de daadwerkelijke vsv’ers ook als zodanig worden geschat. Daarnaast geeft de precision aan hoeveel procent van de geschatte vsv’ers dit ook werkelijk zijn. De F1-score vat beide maten samen. Op basis van de uitkomsten uit stap 2 en 3 wordt een voorkeursmodel bepaald.
Stap 4: Multilevel analyse
Een aanname van het logistische regressiemodel is dat een specifieke jongere wel of niet vsv’er wordt, onafhankelijk van alle andere jongeren in de populatie. Aangezien jongeren geclusterd zijn binnen scholen en binnen RMC-regio’s, zou het mogelijk kunnen zijn dat niet aan deze aanname wordt voldaan. Het zou bijvoorbeeld kunnen dat twee jongeren die op dezelfde school zitten relatief vaker of juist relatief minder vaak - afhankelijk van de school - allebei vsv’er worden dan twee jongeren die niet op dezelfde school zitten. Als dit het geval is, kan een betere beschrijving van de data worden verkregen door het logistische regressiemodel uit te breiden met een zogenaamde multilevel-component. Zie bijlage 4.2 voor meer informatie over multilevel analyse.
Om te onderzoeken of het logistische model een dergelijke aanpassing nodig heeft, wordt er eerst onderzocht of er in het voorkeursmodel inderdaad sprake is van clustering. Voor leerlingen in het vo zijn multilevel-modellen getest met een clustering op schoolniveau, op regionaal niveau en met een combinatie van beide typen clustering naast elkaar. Voor studenten in het mbo is geen clustering op schoolniveau onderzocht. Mbo-scholen bestaan vaak uit meerdere, inhoudelijk verschillende, en vaak ook regionaal verspreide vestigingen (soms zelfs over meerdere RMC-regio’s). Gegevens over inschrijvingen op vestigingsniveau zijn voor het mbo momenteel nog niet beschikbaar. Clustering op schoolniveau is voor het mbo dus niet zinvol terwijl clustering op vestigingsniveau op dit moment nog niet onderzocht kan worden. Voor het mbo is daarom alleen clustering op het niveau van RMC-regio onderzocht.
Om te evalueren in hoeverre clustering voorkomt in de data – en daarmee in hoeverre een multilevel-model hier toegevoegde waarde heeft boven een gewoon logistisch regressiemodel – kijken we in dit onderzoek naar het mediane effect van de clustering op de kansverhoudingen (ook wel median odds ratio (MOR) genoemd). De interpretatie van de MOR is vergelijkbaar met die van de eerdergenoemde odds ratio’s, zie bijlage 4.2.2 voor details.
Ten slotte is het belangrijk om op te merken dat, indien er inderdaad sprake is van clustering, dit niet betekent dat de geschatte odds ratio’s uit een logistisch regressiemodel zonder multilevel-component vertekend zijn. Wel kan een multilevel analyse in dat geval mogelijk helpen om nauwkeurigere schattingen van deze odds ratio’s te vinden.
Extra analyses
Tot slot zijn er ook nog extra analyses uitgevoerd. Ten eerste is het voorkeursmodel gevalideerd op het DUO-cohort, door de stepwise analyse (stap 2) ook op die populatie toe te passen. Daarbij wordt zowel de volgorde als de selectie van kenmerken opnieuw bepaald. Op deze manier kunnen de modellen gebaseerd op de CBS- en de DUO-data vergeleken worden.
Daarnaast gebruiken we, vooruitlopend op fase 2 van het onderzoek, het voorkeursmodel voor vo en mbo om een eerste beeld te schetsen van het aantal geschatte vsv’ers per RMC-regio. Daarbij kan op RMC-regio niveau een eerste indruk verkregen worden van de modelkwaliteit, door het werkelijk aandeel vsv’ers te vergelijken met het door het model geschatte aandeel vsv’ers. Hierbij wordt gebruikt gemaakt van een simpele aggregatie (optelling) van de geschatte kansen. In fase 2 zullen bepaalde keuzes rondom de aggregatie gemaakt worden door het ministerie van OCW. Dit zal leiden tot een definitief beeld van het aantal geschatte vsv’ers per RMC-regio.
2) Cramérs V wordt berekend via de volgende formule: \( V = \sqrt{\frac{X^2}{n(r-1)}} \), waarbij \( X^2 \) de chi-kwadraat-toetsingsgrootheid is voor de hypothese dat er geen samenhang bestaat tussen het achtergrondkenmerk en vsv, \( n \) het aantal waarnemingen en \( r \) het aantal categorieën van het achtergrondkenmerk (Agresti, 2013, p. 110).
3. Ontwikkeling model voor het vo
3.1 Inleiding
In dit hoofdstuk bespreken we de totstandkoming van het model waarmee voor het vo op leerlingniveau de kans op voortijdig schoolverlaten (vsv) kan worden geschat volgens de aanpak zoals beschreven in paragraaf 2.7. De eerste stap betreft de selectie van achtergrondkenmerken op basis van beschrijvende en bivariate analyses. In de tweede stap wordt een stepwise selectieprocedure toegepast op het cohort 2018/’19 en op het validatiecohort 2017/’18. Vervolgens bespreken we in de derde stap de resultaten van de kruisvalidaties. Bovendien onderzoeken we in de vierde stap of het model met multilevel-component toegevoegde waarde heeft. Tot slot presenteren we in de laatste paragraaf een vergelijking van de modelschattingen op basis van een DUO-cohort en een eerste beeld van de resultaten op het niveau van RMC-regio.
3.2 Stap 1: Voorselectie kenmerken
Om het effect van de achtergrondkenmerken, zoals beschreven in paragraaf 2.5, te onderzoeken is er een voorselectie gemaakt op basis van beschrijvende statistieken en bivariate analyses. Op basis van deze analyses zijn er keuzes gemaakt in de codering van de variabelen, zijn referentiecategorieën bepaald en is een keuze gemaakt bij (inhoudelijk) vergelijkbare kenmerken.
De belangrijkste wijzigingen zijn hier uitgelicht:
- Ongeoorloofd verzuim: vsv kwam zeer beperkt voor in de groep leerlingen die doorverwezen was naar Halt wegens overtreding van de leerplicht. Dit is niet wenselijk bij het uitvoeren van regressieanalyses, omdat dit kan leiden tot onbetrouwbare en moeilijk te interpreteren resultaten. Het kenmerk is daarom niet meegenomen in de verdere analyses.
- Huishoudinkomen onder de lage inkomensgrens: Dit kenmerk overlapt sterk met de welvaartspercentielen, waardoor we, op advies van een inhoudelijk expert van het CBS, uiteindelijk ervoor hebben gekozen om de welvaartspercentielen mee te nemen in de verdere analyses in plaats van deze variabele. Dit kenmerk bevat daarnaast alleen inkomen, terwijl de welvaartspercentielen ook rekening houden met het vermogen. Hetzelfde geldt voor het kenmerk op buurtniveau.
- Lage welvaart in het huishouden: Omdat de welvaartspercentielen in vijf categorieën een vollediger beeld geven dan alleen het laagste percentiel, is er voor gekozen de lage welvaart niet mee te nemen in de verdere analyses.
- Aantal gewerkte uren: Het hebben van een bijbaan kan – theoretisch gezien – de kans op vsv zowel vergroten als verkleinen. Dit kenmerk is daarom lastig te interpreteren en werkelijke effecten kunnen daardoor vertekend zijn. Daarom is besloten dit kenmerk niet mee te nemen in verdere analyses.
- Problematische schulden: Omdat vo-leerlingen meestal jonger zijn dan 18 jaar kunnen ze geen persoonlijke schulden hebben binnen de definitie zoals beschreven in bijlage 3. Daarom nemen we enkel de schulden op huishoudniveau mee voor het vo. Dit betekent dat de indeling van dit kenmerk is aangepast voor het vo naar twee categorieën: geen problematische schulden (0) en wel problematische schulden (1) in het huishouden.
3.3 Stap 2: Stepwise analyse
Na de voorselectie van kenmerken is er een stepwise procedure toegepast om de kenmerken te selecteren die het beste model vormen. Dit is gedaan met de forward en backward search en een combinatie van beide. Uiteindelijk zijn de modelschattingen van de methoden vergeleken. Het doel is om een compact model over te houden, met voldoende verklaringskracht. Waar de forward methode kenmerken stapsgewijs toevoegt, verwijdert de backward methode deze stapsgewijs. De forward methode stopt als er geen modelverbetering meer optreedt op basis van de BIC-waarde. De backward methode doet hetzelfde bij het verwijderen van de kenmerken. De forward methode leverde in de analyses een compactere selectie kenmerken op dan de backward methode, waardoor deze stepwise methode als uitgangspunt is genomen voor de verdere selectie van kenmerken. Bovendien lagen zowel de BIC als de pseudo-R2-maten voor beide methoden dicht bij elkaar (forward: BIC = 61313, McKelveyZavoina R2 = 0,36; backward: BIC = 61291, McKelveyZavoina R2 = 0,37).
De forward analyse resulteerde in de volgende selectie van kenmerken, in volgorde van toegevoegde waarde voor het model:
- Leeftijd van de leerling
- Onderwijssoort
- Vertraging
- Ouderlijke structuur
- Welvaart
- Verdachte van een misdrijf
- Problematische schulden in huishouden
- Geslacht
- Langdurige gezondheidsproblemen
- Psychosociale problemen moeder
Na de selectie van het tiende kenmerk stopte de stepwise procedure, omdat er volgens het model geen extra verklaringskracht meer werd toegevoegd.
De forward methode voegt telkens één kenmerk toe aan het model. Per stap in deze methode is de BIC uitgerekend om te bepalen in hoeverre er nog modelverbetering optreedt, zie figuur 3.3.1. Hierbij geldt dat een lagere BIC-waarde een betere modelkwaliteit betekent.
| volgorde volgens stepwise selectie | BIC-waarde (BIC-waarde) |
|---|---|
| 0 | 86573,8 |
| 1 | 68599,2 |
| 2 | 62958,0 |
| 3 | 62416,7 |
| 4 | 61986,5 |
| 5 | 61688,0 |
| 6 | 61485,1 |
| 7 | 61429,9 |
| 8 | 61377,4 |
| 9 | 61341,1 |
| 10 | 61337,0 |
De figuur laat zien dat hoe meer kenmerken er worden opgenomen, hoe lager de BIC wordt en des te beter het totale model de kans op vsv dus kan schatten. De grootste afname van de BIC ligt bij het model met de eerste twee kenmerken, wat te zien is aan de ‘knik’ in de figuur. De volgende knik in de daling ligt rond het model met vijf kenmerken, gevolgd door het model met zeven kenmerken. Daarna vlakt de lijn van de BIC af; de modelkwaliteit neemt bij het toevoegen van de laatste kenmerken nauwelijks nog toe.
Daarnaast is de stabiliteit van het model onderzocht door de forward stepwise procedure toe te passen op het validatiecohort (2017/’18). Er is dus opnieuw een stepwise procedure toegepast, waarbij opnieuw bepaald werd welke modelkenmerken relevant zijn voor dat cohort. Vervolgens konden de geselecteerde kenmerken en hun volgorde vergeleken worden tussen de twee cohorten. De resultaten worden weergegeven in tabel 3.3.2.
| Volgorde | Basiscohort (2018/’19) | Validatiecohort (2017/’18) |
|---|---|---|
| 1 | Leeftijd van de leerling | Leeftijd van de leerling |
| 2 | Onderwijssoort | Onderwijssoort |
| 3 | Vertraging | Vertraging |
| 4 | Ouderlijke structuur | Ouderlijke structuur |
| 5 | Welvaart | Welvaart |
| 6 | Verdachte van een misdrijf | Verdachte van een misdrijf |
| 7 | Problematische schulden in huishouden | Problematische schulden in huishouden |
| 8 | Geslacht | Acute gezondheidsproblemen |
| 9 | Langdurige gezondheidsproblemen | Hoogst behaalde opleidingsniveau moeder |
| 10 | Psychosociale problemen moeder | Herkomstland leerling |
De selectie en volgorde van de eerste zeven kenmerken zijn in beide cohorten identiek. Daarna zijn er verschillen te zien tussen beide modellen. Dit komt overeen met het beeld in figuur 3.3.1. De verandering in de BIC-waarden was bij de laatste modellen zo klein dat het toevoegen van extra kenmerken aan het model willekeuriger wordt.
3.4 Stap 3: Kruisvalidaties
Na de stepwise analyse zijn er als derde stap kruisvalidaties uitgevoerd met de volgorde van kenmerken zoals beschreven in paragraaf 3.3. Tijdens deze analyse werd er eerst een leeg model geschat, om te onderzoeken wat de modelkwaliteit was zonder verklarende kenmerken. Daarna is er herhaaldelijk een nieuw model geschat waarbij telkens een extra kenmerk is toegevoegd op basis van de eerder vastgestelde volgorde. Uiteindelijk resulterend in het complete model met de tien kenmerken in het laatste model.
De kruisvalidaties zijn geëvalueerd met behulp van de fitmaten zoals beschreven in de bijlages 4.1.2 en 4.1.3 en worden weergegeven in tabel 3.4.1. Om de recall-, precision- en F1-waarde te kunnen berekenen zijn leerlingen ingedeeld in twee categorieën: geen vsv (0), en wel vsv (1). Dit is gedaan met een grenswaarde, zoals beschreven in bijlage 4.1.3. Bij de daadwerkelijke toepassing van het model zullen we niet gaan werken met een classificatie van 0 of 1, maar met de daadwerkelijke kansen per leerling om vsv’er te worden (waarde tussen 0 en 1). Deze fitmaten geven dus vooral een globaal beeld van de modelkwaliteit en dienen gebruikt te worden voor onderlinge modelvergelijkingen. Dit geldt niet voor de (relatieve) entropie en gemiddelde R2.
| Model | Entropie | Relatieve entropie1) | Gemiddelde R2 2) | Recall | Precision | F1 |
|---|---|---|---|---|---|---|
| Intercept3) | 43 280 | . | . | . | . | . |
| 1 | 34 264 | 0,208 | 0,320 | 0,807 | 0,028 | 0,055 |
| 2 | 31 405 | 0,274 | 0,406 | 0,726 | 0,057 | 0,106 |
| 3 | 31 121 | 0,281 | 0,352 | 0,749 | 0,053 | 0,099 |
| 4 | 30 895 | 0,286 | 0,352 | 0,769 | 0,046 | 0,086 |
| 5 | 30 717 | 0,290 | 0,360 | 0,813 | 0,038 | 0,072 |
| 6 | 30 609 | 0,293 | 0,360 | 0,815 | 0,038 | 0,072 |
| 7 | 30 576 | 0,294 | 0,360 | 0,815 | 0,038 | 0,073 |
| 8 | 30 544 | 0,294 | 0,362 | 0,834 | 0,035 | 0,067 |
| 9 | 30 519 | 0,295 | 0,362 | 0,835 | 0,035 | 0,066 |
| 10 | 30 510 | 0,295 | 0,362 | 0,775 | 0,047 | 0,089 |
| 1) De relatieve entropie staat ook wel bekend als de McFadden (1974) pseudo-R2-waarde en kan daarbij ook vergeleken worden met de gemiddelde R2. 2) We geven de gemiddelde R2 weer, omdat deze per groep in de kruisvalidatie wordt berekend zoals beschreven in Bijlage 4.1.2. 3) Voor het intercept model worden geen fitmaten (excl. de entropie) weergegeven, omdat deze geen informatieve waarde hebben in de vergelijking van de modellen met kenmerken. | ||||||
In de tabel zien we dat de entropie-waarde afneemt, naarmate het model uitgebreider wordt. Dit betekent dat hoe uitgebreider het model, des te beter het model wordt in het schatten van de kans op vsv. De relatieve entropie geeft de relatieve verbetering ten opzichte van het lege model weer. De toename blijft oplopen, maar vlakt af rond het model met zeven kenmerken.
De recall-waarde ligt tussen de 0,73 en 0,84. Dit betekent dat het model de leerlingen die werkelijk vsv’er worden vaak als zodanig classificeert. De precision ligt echter tussen de 0,03 en 0,06 in, wat een relatief lage waarde is, maar die wel in lijn is met het lage aandeel vsv’ers in de populatie (0,8% op het vo, zie ook paragraaf 2.4). De precision laat zien dat de modellen met achtergrondkenmerken het een stuk beter doen dan een leeg model. Stel de achtergrondkenmerken worden niet meegenomen en iedereen zou als vsv’er geclassificeerd worden, dan zou de precision gelijk zijn aan het aandeel vsv’ers in de vo populatie, dus 0,008. Dan is een precision van 0,03 tot 0,06 weer een relatieve verbetering. De F1-waarde vat bovenstaande resultaten van de recall- en precision-waarde samen.
De gemiddelde McKelveyZavoina R2 over de vijf kruisvalidaties ligt tussen de 0,32 en 0,41, maar ligt voor de meeste modelvarianten dicht bij elkaar. Deze R2 variant moet met voorzichtigheid worden geïnterpreteerd en de grootte van het effect is daarbij ook context-afhankelijk. We gebruiken de R2 in de kruisvalidaties dan ook voornamelijk om modelvergelijkingen te maken. Daaraan zien we dat model twee de hoogste waarde heeft. Voor de overige modellen ligt de waarde wat lager en loopt de waarde op naarmate het model uitgebreider wordt. Omdat een model met twee kenmerken wel erg beperkt is en weinig inzicht geeft in de achtergrondkenmerken die bijdragen aan het risico op vsv, gaat de voorkeur uit om naar de uitgebreidere varianten te kijken.
3.5 Conclusie modelselectie
Op basis van bovenstaande resultaten is een definitief voorkeursmodel voor het vo geselecteerd. Het is daarbij van belang om een model te selecteren op basis van de modelkwaliteit en stabiliteit. Daarnaast wil je een zo informatief mogelijk model, dat toch eenvoudig, transparant en goed uit te leggen blijft. Op basis van deze criteria is het model met zeven kenmerken gekozen. Ten eerste zien we in figuur 3.3.1 dat de BIC-waarde niet veel verder afneemt na zeven kenmerken. Ten tweede zien we dat de selectie en volgorde van de eerste zeven kenmerken stabiel blijven tussen de twee onderzochte cohorten. Ook blijkt uit stap 3 dat de modelkwaliteit bij zeven kenmerken vergelijkbaar blijft met modellen die uitgebreider zijn. Het verder uitbreiden van het model heeft dan ook weinig toegevoegde waarde. Indien een verdere versimpeling van het model door OCW gewenst is en in fase 2 vergelijkbare resultaten oplevert met het voorkeursmodel, zou eventueel gekozen kunnen worden voor het model met vijf kenmerken (ook wel het “back-upmodel” genoemd). De coëfficiënten en Odds Ratio’s (OR) behorende tot het model met vijf en zeven kenmerken worden weergegeven in bijlage 5.
Met behulp van de gegevens in figuur 3.5.1 kan een voorbeeld gegeven worden van de toepassing van de odds ratio’s voor een fictieve leerling. Deze leerling heeft bepaalde kenmerken, zoals een leeftijd van 19 jaar of ouder en een lage welvaart. Elke categorie waarin een leerling valt, heeft een odds ratio ten opzichte van de referentiecategorie. Door vervolgens deze met elkaar te vermenigvuldigen, komen we uit op de odds op vsv van de betreffende leerling. Zie paragraaf 2.7 voor een uitgebreidere uitleg van odds en odds ratio’s. Volgens de figuur is de kans op vsv voor die leerling 1,303 keer zo groot als de kans op geen vsv. Bij deze kansverhouding hoort een geschatte kans op vsv van 0,566. De kans dat een leerling met deze combinatie van achtergrondkenmerken vsv’er wordt is dus 56,6%.
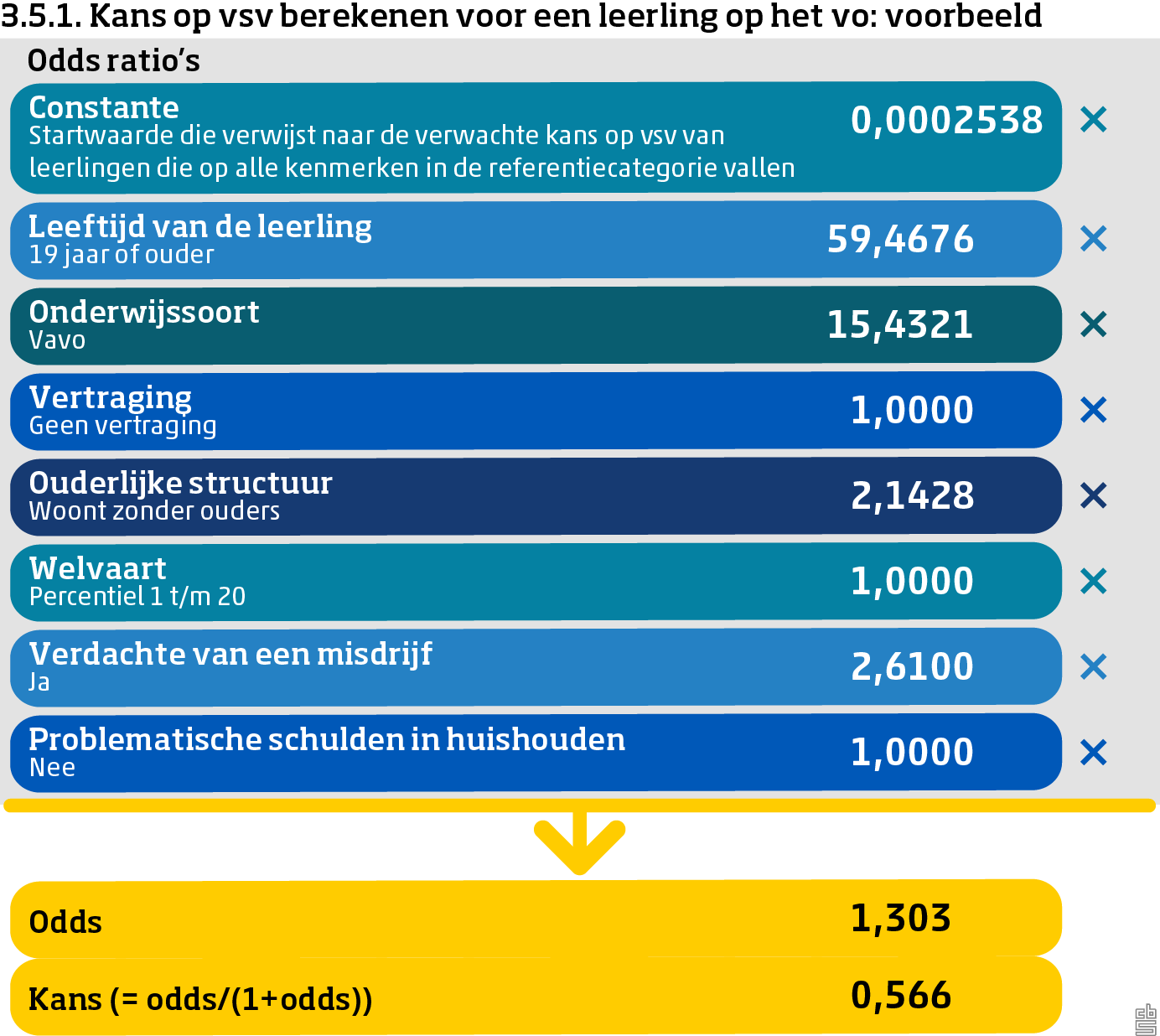
3.6 Stap 4: Uitbreiding met multilevel-component
Leerlingen zijn geclusterd binnen scholen en scholen zijn weer geclusterd binnen RMC-regio’s. Zoals eerder is opgemerkt in paragraaf 2.7 zou het kunnen dat twee jongeren die op dezelfde school zitten of binnen dezelfde regio naar school gaan relatief vaker allebei wel of allebei geen vsv’er worden dan twee jongeren op verschillende scholen of uit verschillende regio’s. Om te onderzoeken hoe sterk dit clustereffect is en of hier in de analyses rekening mee gehouden dient te worden, hebben we in stap 4 multilevel modellen geschat.
Allereerst is gekeken naar clustering op het hoogste niveau, te weten RMC-regio. In een model waarin alleen een random intercept op RMC-regioniveau is opgenomen was de Median Odds Ratio (MOR) 1,30 (95% betrouwbaarheidsinterval (BI): 1,23-1,41). Dat wil zeggen dat wanneer een leerling verhuist van een RMC-regio met een lagere odds op vsv naar een RMC-regio met een hogere odds op vsv, de mediane odds op vsv 1,3 keer zo groot zijn. Aangezien de MOR een odds ratio is, kan hij ook direct vergeleken worden met de andere odds ratio’s van de variabelen in het model. In verhouding is dit effect van RMC-regio dusdanig klein, dat wij hebben besloten hier in de modelontwikkeling geen rekening mee te houden. Aanvullend is wel nog onderzocht of deze MOR nog kleiner werd na het toevoegen van de zeven geselecteerde verklarende variabelen, wat inderdaad het geval was.
Vervolgens is de clustering binnen scholen onderzocht. In het model met alleen een random intercept op schoolniveau was de MOR 2,91 (95% BI:2,72-3,13). Het schooleffect is dus aanzienlijk groter dan het effect van RMC-regio, d.w.z. er is een veel sterkere clustering binnen scholen dan binnen RMC-regio’s. Vervolgens zijn aan het model met het random intercept op schoolniveau de zeven geselecteerde verklarende variabelen toegevoegd. Na toevoeging van deze variabelen was de MOR nog maar 1,45 (95% BI:1,40-1,51). De variabelen konden de clustering binnen de scholen dus al voor een groot deel verklaren. Verder hebben we de geschatte coëfficiënten van de verklarende variabelen vergeleken tussen het model met een random intercept op schoolniveau en het model zonder multilevel-component. Er waren geen duidelijke verschillen zichtbaar tussen deze geschatte coëfficiënten, wat betekent dat de geschatte kansen op vsv uit beide modellen in de praktijk dicht bij elkaar zouden liggen. Daarom is besloten dat in de modelontwikkeling geen rekening hoeft te worden gehouden met de clustering binnen scholen. De conclusie is dat een multilevel component niet nodig is voor het vo model.
Bij het validatiecohort vonden wij vergelijkbare resultaten. In het model met alleen een random intercept op het niveau van RMC-regio was de MOR 1,31 (95% BI:1,23-1,42). In het model met alleen een random intercept op schoolniveau was de MOR 2,96 (95% BI:2,77-3,19) en na toevoeging van de zeven verklarende variabelen nog maar 1,47 (95% BI:1,41-1,53).
Hoewel de gevonden clusteringseffecten klein zijn, zijn ze wel statistisch significant. Hierbij moet worden bedacht dat de onderzoekspopulatie een groot aantal waarnemingen bevat waardoor de kans op statistisch significante resultaten wordt vergroot.
3.7 Extra analyses
Tot slot zijn er twee aanvullende analyses uitgevoerd. Ten eerste hebben we, om de resultaten van het model te valideren, ook een vergelijkbare analyse uitgevoerd op basis van DUO-data. Zoals beschreven in de inleiding van dit rapport, hanteert DUO een andere definitie voor zowel vsv als de populatie dan het CBS. We willen deze data daarom vooral gebruiken om te zien of een model op basis van DUO-data tot een vergelijkbare selectie en volgorde van kenmerken komt als met CBS-data. Om de resultaten te valideren, is de stepwise procedure daarom opnieuw toegepast.
In tabel 3.7.1 worden de resultaten vergeleken. De stepwise procedure resulteert voor de DUO-data in een selectie van twaalf kenmerken, in vergelijking met tien op basis van de CBS-data. De top negen van kenmerken is vergelijkbaar tussen beide modellen. Wel verschuift de volgorde onderling wat. Daarnaast komt het tiende kenmerk uit de CBS-data wel terug op plaats twaalf in de DUO-data en zijn de psychosociale problemen van de leerling en of ouders wanbetaler van de ZVW-premie er als kenmerk bij gekomen.
Zoals in paragraaf 3.5 besproken is het model met zeven kenmerken ons voorkeursmodel. De eerste zeven kenmerken komen overeen tussen beide datasets; er is slechts lichte verschuiving in de volgorde van de kenmerken. Het is daarbij belangrijker dat dezelfde kenmerken geselecteerd worden dan dat dit in exact dezelfde volgorde gebeurt. Op basis van deze analyse concluderen wij dan ook dat beide datasets tot dezelfde selectie van kenmerken leiden.
| Volgorde | Kenmerken (CBS 2018/’19) | Kenmerken (DUO 2018/’19) |
|---|---|---|
| 1 | Leeftijd van de leerling | Leeftijd van de leerling |
| 2 | Onderwijssoort | Onderwijssoort |
| 3 | Vertraging | Ouderlijke structuur |
| 4 | Ouderlijke structuur | Verdachte van een misdrijf |
| 5 | Welvaart | Vertraging |
| 6 | Verdachte van een misdrijf | Problematische schulden in huishouden |
| 7 | Problematische schulden in huishouden | Welvaart |
| 8 | Geslacht | Geslacht |
| 9 | Langdurige gezondheidsproblemen | Langdurige gezondheidsproblemen |
| 10 | Psychosociale problemen moeder | Psychosociale problemen leerling |
| 11 | Wanbetaler ZVW premie (ouders) | |
| 12 | Psychosociale problemen moeder | |
Ten tweede hebben we op basis van het eindmodel met zeven kenmerken voor de totale populatie op het vo een simpele aggregatie uitgevoerd van de geschatte kansen op vsv. Dit betekent dat de geschatte kansen van alle leerlingen in een bepaalde RMC-regio bij elkaar zijn opgeteld. Hiermee krijgen we al een eerste indicatie van de verschillen tussen het werkelijk en geschatte aantal vsv’ers en hoe dit tussen regio’s verschilt. In fase 2 van dit onderzoek zal deze aggregatie naar RMC-niveau uitvoerig onderzocht worden. Hierbij zullen ook verschillende beleidskeuzes door het ministerie van OCW gemaakt moeten worden.
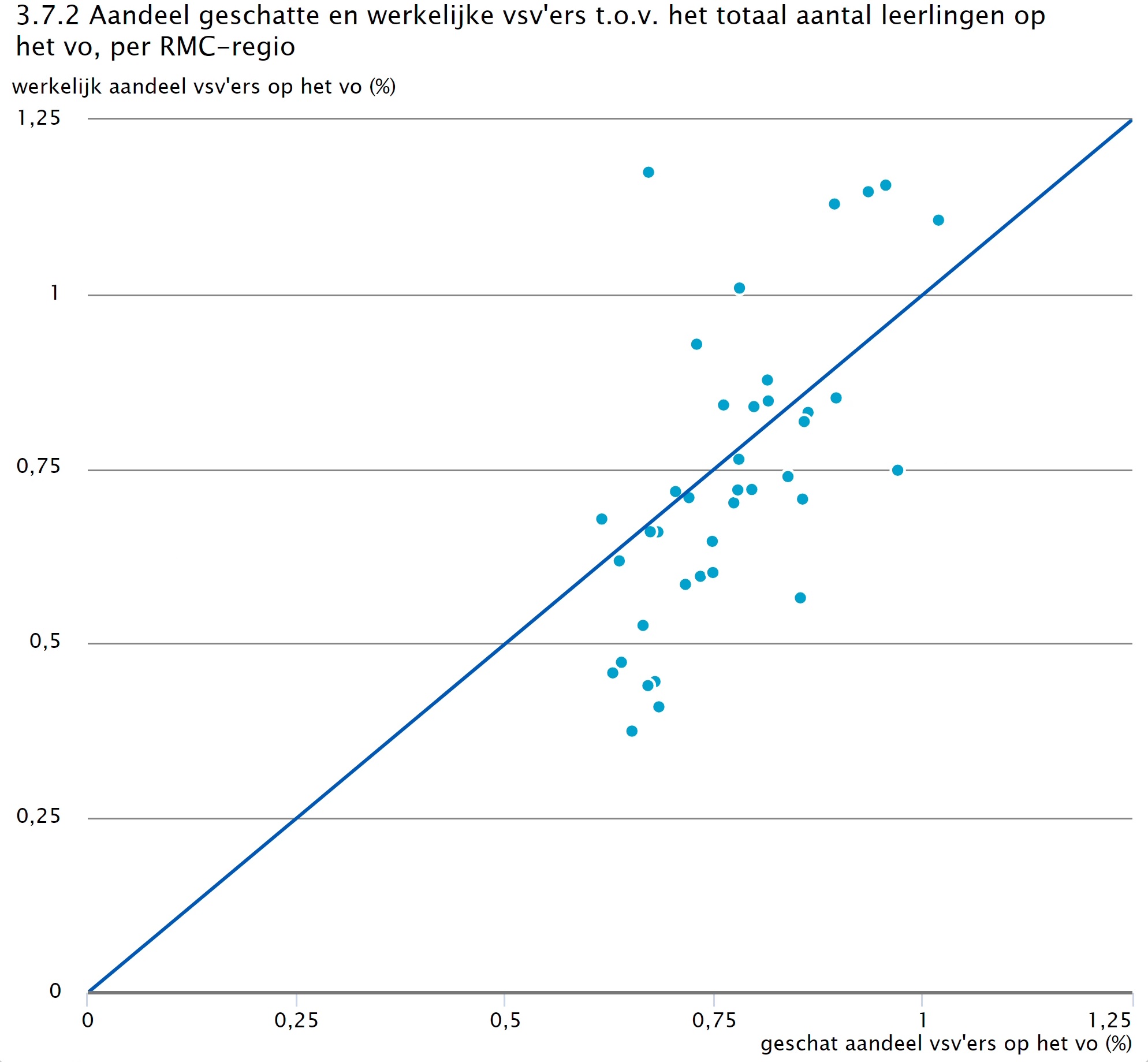
Om een eerste indicatie te geven van de samenhang tussen het werkelijke en geschatte aantal vsv’ers per RMC-regio op het vo, hebben we de Pearson correlatiecoëfficiënt uitgerekend. Deze geeft een sterke samenhang aan tussen het werkelijke en geschatte aantal vsv’ers met \( \rho \)= 0,974. Omdat aantallen afhankelijk zijn van het aantal leerlingen op RMC-regio, hebben we in figuur 3.7.2 de aantallen uitgedrukt als percentage van het totaal aantal leerlingen per regio. Het totaal aantal leerlingen is gedefinieerd zoals in dit gehele rapport: leerlingen zonder startkwalificatie. Daarbij is te zien dat er wat minder spreiding is tussen regio’s in de geschatte waarden t.o.v. in de werkelijke waarden. Ook is te zien dat er vaker een overschatting is van de werkelijke waarde (onder de blauwe lijn) dan een onderschatting (boven de blauwe lijn). Wat de mogelijke oorzaken hiervan zijn, wordt in fase 2 van het onderzoekstraject onderzocht.
4. Ontwikkeling model voor het mbo
4.1 Inleiding
In dit hoofdstuk bespreken we de totstandkoming van het model waarmee op studentniveau de kans op vsv kan worden geschat voor het mbo volgens de aanpak zoals beschreven in paragraaf 2.7. Net zoals bij het vo, zullen we als eerste stap de selectie van achtergrondkenmerken beschrijven met behulp van beschrijvende en bivariate analyses. In de tweede stap wordt een stepwise selectieprocedure toegepast op het cohort 2018/’19 en op het validatiecohort 2017/’18. Als derde stap bespreken we de resultaten uit de kruisvalidaties. Ook onderzoeken we de toegevoegde waarde van een multilevel component als vierde stap. Tot slot presenteren we in de laatste paragraaf een vergelijking van de modelschattingen op basis van een DUO-cohort en een eerste beeld van de resultaten op RMC-regio niveau.
4.2 Stap 1: Voorselectie kenmerken
Op basis van beschrijvende statistieken en bivariate analyses hebben we een voorselectie gemaakt van de achtergrondkenmerken uit paragraaf 2.5 voor het mbo. Op basis van deze analyses zijn er keuzes gemaakt in de codering van variabelen, zijn referentiecategorieën bepaald en is een keuze gemaakt bij (inhoudelijk) vergelijkbare kenmerken.
De belangrijkste wijzigingen zijn hier uitgelicht:
- Inkomen onder de lage inkomensgrens: Dit kenmerk overlapt sterk met de welvaartspercentielen, waardoor we hebben gekozen om de welvaartspercentielen mee te nemen in plaats van deze variabele. Dit kenmerk bevat daarnaast alleen inkomen, terwijl de welvaartspercentielen ook rekening houden met het vermogen. Hetzelfde geldt voor het kenmerk op buurtniveau.
- Lage welvaart in het huishouden: Omdat de welvaartspercentielen in vijf categorieën een vollediger beeld geven dan alleen het laagste percentiel, is er voor gekozen de lage welvaart niet mee te nemen in de verdere analyses.
- Problematische schulden: Voor het mbo maken we onderscheid in drie categorieën in tegenstelling tot de twee categorieën zoals beschreven bij het vo: geen problematische schulden (0), problematische schulden in het huishouden (1), en problematische schulden op persoonsniveau (2). Omdat studenten op het mbo wel persoonlijke schulden kunnen hebben volgens de definitie van bijlage 3, is hier een aparte categorie toegevoegd voor het mbo.
- Mbo richting sectorkamer: Dit kenmerk bevatte veel kleine groepen, daarom is er voor gekozen opleidingsrichting volgens ISCED-indeling mee te nemen, zoals beschreven in bijlage 3. Bovendien is de ISCED-indeling stabieler beschikbaar over de tijd.
- Aantal jaren op het mbo: Omdat het mbo uit verschillende niveaus bestaat en variatie kent in de duur van de opleiding, is het aantal jaren op het mbo geen duidelijke indicator voor vsv. We nemen dit kenmerk daarom niet mee in de vervolganalyses.
4.3 Stap 2: Stepwise analyse
Na de voorselectie van kenmerken is er een stepwise procedure toegepast om zo een verdere selectie te maken van de achtergrondkenmerken. Dit is net zoals bij het vo gedaan met een forward, backward, en gecombineerde aanpak. We selecteren uiteindelijk een model dat eenvoudig en transparant is, maar ook voldoende verklaringskracht heeft. Ook bij het mbo komt het meest compacte model uit de forward methode en is er geen tot weinig verschil te zien met de backward methode (forward: BIC = 167450, McKelveyZavoina R2 = 0,28; backward: BIC = 167436, McKelveyZavoina R2 = 0,28).
De forward analyse resulteerde in de volgende selectie van kenmerken, in volgorde van belang voor het model:
- Mbo-niveau
- Leeftijd van de student
- Ouderlijke structuur
- Verdachte van een misdrijf
- Geslacht
- Hoogst behaalde opleidingsniveau moeder
- Problematische schulden
- Leerweg
- Onderwijsrichting volgens ISCED
- Welvaart
- Psychosociale problemen student
- Stedelijkheid van de buurt
- Hoogst behaalde opleidingsniveau vader
- Niveau van vooropleiding
- Herkomstland moeder
- Langdurige gezondheidsproblemen
- Wanbetaler ZVW-premie (ouders)
- Verblijfsduur van moeder in Nederland
- Acute gezondheidsproblemen
- Psychosociale problemen moeder
- Migratieachtergrond vader
Na de selectie van het 21e kenmerk stopte de stepwise procedure, omdat er volgens het model geen extra verklaringskracht meer werd toegevoegd.
Bij de forward methode wordt er telkens één kenmerk toegevoegd aan het model. Per stap in deze methode is de BIC uitgerekend om te bepalen in hoeverre er nog modelverbetering optreedt. Figuur 4.3.1 laat de ontwikkeling van de BIC-waarde zien gedurende de stepwise procedure. Hierbij geldt dat een lagere BIC-waarde een betere modelkwaliteit betekent.
| volgorde volgens stepwise selectie | BIC-waarde (BIC-waarde) |
|---|---|
| 0 | 194960,4 |
| 1 | 183039,2 |
| 2 | 175702,3 |
| 3 | 173946,9 |
| 4 | 172530,5 |
| 5 | 171537,3 |
| 6 | 170456,2 |
| 7 | 169742,6 |
| 8 | 169193,4 |
| 9 | 168580,9 |
| 10 | 168216,0 |
| 11 | 168033,6 |
| 12 | 167860,4 |
| 13 | 167742,4 |
| 14 | 167644,8 |
| 15 | 167582,8 |
| 16 | 167529,3 |
| 17 | 167499,6 |
| 18 | 167476,2 |
| 19 | 167460,6 |
| 20 | 167454,4 |
| 21 | 167450,2 |
In de figuur is te zien dat de BIC daalt wanneer er meer kenmerken worden toegevoegd aan het model. De sterkste daling zit in het begin van de figuur, aan het einde van de figuur vlakt de daling af. De modelkwaliteit neemt na het toevoegen van het twaalfde kenmerk nog nauwelijks toe. In de verdere analyses hebben we kenmerk 21, de migratieachtergrond van de vader, vervangen door die van de moeder. Dit zal in combinatie met kenmerk vijftien, het herkomstland van de moeder, een consistenter beeld geven.
Daarnaast is de forward stepwise procedure toegepast op het validatiecohort (2017/’18) om de stabiliteit van het model te onderzoeken. Er is dus opnieuw een stepwise procedure toegepast. Hierbij is weer opnieuw bepaald welke modelkenmerken relevant zijn voor dat cohort. Omdat het mbo-model uit de stepwise procedure meer kenmerken heeft in vergelijking met het vo-model, zal het ook lastiger zijn om dezelfde stabiliteit te behouden met zo’n groot model. De resultaten van de vergelijking worden weergegeven in tabel 4.3.2.
| Volgorde | Basiscohort (2018/’19) | Validatiecohort (2017/’18) |
|---|---|---|
| 1 | Mbo-niveau | Mbo-niveau |
| 2 | Leeftijd van de student | Leeftijd van de student |
| 3 | Ouderlijke structuur | Problematische schulden |
| 4 | Verdachte van een misdrijf | Ouderlijke structuur |
| 5 | Geslacht | Verdachte van een misdrijf |
| 6 | Hoogst behaalde opleidingsniveau moeder | Geslacht |
| 7 | Problematische schulden | Hoogst behaalde opleidingsniveau moeder |
| 8 | Leerweg | Stedelijkheid van de buurt |
| 9 | Onderwijsrichting volgens ISCED | Leerweg |
| 10 | Welvaart | Onderwijsrichting volgens ISCED |
| 11 | Psychosociale problemen student | Welvaart |
| 12 | Stedelijkheid van de buurt | Psychosociale problemen student |
| 13 | Hoogst behaalde opleidingsniveau vader | Herkomstland student |
| 14 | Niveau van vooropleiding | Niveau van vooropleiding |
| 15 | Herkomstland moeder | Langdurige gezondheidsproblemen |
| 16 | Langdurige gezondheidsproblemen | Hoogst behaalde opleidingsniveau vader |
| 17 | Wanbetaler ZVW premie (ouders) | Psychosociale problemen moeder |
| 18 | Verblijfsduur van moeder in Nederland | Wanbetaler ZVW premie (ouders) |
| 19 | Acute gezondheidsproblemen | Acute gezondheidsproblemen |
| 20 | Psychosociale problemen moeder | |
| 21 | Migratieachtergrond moeder | |
De kenmerken in de top twaalf zijn hetzelfde voor beide cohorten. Wel verschuiven problematische schulden en stedelijkheid van de buurt naar een andere positie binnen de top twaalf. Vanaf positie twaalf verschillen de kenmerken meer tussen de cohorten, wat het model instabieler maakt. Bovendien zien we in figuur 4.3.1, dat er vanaf twaalf kenmerken weinig extra toegevoegde waarde is in de verklaringskracht van het model.
Stepwise analyses naar mbo-niveau
In de vorige paragraaf zagen we dat mbo-niveau als eerste werd geselecteerd in de stepwise selectie. Mbo-niveau bestaat uit entreeopleiding en niveau 2, 3 en 4. Uit eerder onderzoek blijkt dat mbo-entree een andere populatiesamenstelling heeft dan de andere mbo-niveaus en ook verschilt op de aanwezigheid van problemen. Ter controle hebben we daarom extra analyses uitgevoerd waarbij vsv op de mbo-entree en mbo niveaus 2-4 als twee aparte modellen worden geschat. De stepwise procedure is daarbij per model opnieuw toegepast.
Uit die analyse bleek dat de modellen inderdaad tot een verschillende selectie van kenmerken kwamen. Het mbo niveau 2-4 model kwam tot grotendeels dezelfde selectie kenmerken als het totale mbo-model en verschilde bij enkele kenmerken alleen in de volgorde. Het mbo-entreeopleiding model kwam daarentegen wel tot een andere selectie van kenmerken en daarbij ook een andere volgorde.
Daarnaast zijn de modellen ook weer toegepast op het validatiecohort. De resultaten lieten echter zien, dat voornamelijk bij het mbo-entree model de kenmerken niet stabiel werden geselecteerd tussen de cohorten. Bij de andere mbo-niveaus waren deze verschillen minder aanwezig. Vanwege deze instabiliteit en de voorkeur van het ministerie van OCW om de ontwikkeling van een nieuw verdeelmodel simpel en transparant te houden, is er daarom in overleg met het ministerie voor gekozen om geen aparte modellen te ontwikkelen. Binnen het totale mbo-model wordt er bovendien nog steeds rekening gehouden met de verschillen binnen de entreeopleiding en andere niveaus doordat mbo-niveau als eerste kenmerk in het model is meegenomen.
4.4 Stap 3: Kruisvalidaties
Naast de stepwise analyses zijn er als derde stap kruisvalidaties uitgevoerd op het totale mbo-model. Tijdens deze analyse is eerst een leeg model geschat, om te onderzoeken wat de modelkwaliteit is zonder verklarende kenmerken. Daarna is er herhaaldelijk een nieuw model geschat waarbij telkens een extra kenmerk is toegevoegd op basis van de eerder vastgestelde volgorde. Uiteindelijk resulteerde dit in het complete model met de 21 kenmerken uit het laatste model van de vorige stap.
De kruisvalidaties zijn geëvalueerd met behulp van de fitmaten zoals beschreven in bijlages 4.1.2 en 4.1.3 en weergegeven in tabel 4.4.1. Voor het berekenen van recall-, precision- en F1-waarde zijn studenten ingedeeld in twee categorieën: geen vsv (0), en wel vsv (1). Dit is gedaan met een grenswaarde, zoals beschreven in bijlage 4.1.3. Bij de daadwerkelijke toepassing van het model zullen we niet gaan werken met een classificatie van 0 of 1, maar met de daadwerkelijke kansen per student om vsv’er te worden. Deze fitmaten geven dus vooral een globaal beeld van de modelkwaliteit en dienen gebruikt te worden voor onderlinge modelvergelijkingen. Dit geldt niet voor de (relatieve) entropie en gemiddelde R2.
| Model | Entropie | Relatieve entropie1) | Gemiddelde R2 2) | Recall | Precision | F1 |
|---|---|---|---|---|---|---|
| Intercept3) | 97 474 | . | . | . | . | . |
| 1 | 91 497 | 0,061 | 0,090 | 0,497 | 0,160 | 0,242 |
| 2 | 87 778 | 0,099 | 0,210 | 0,586 | 0,167 | 0,260 |
| 3 | 86 889 | 0,109 | 0,230 | 0,674 | 0,153 | 0,250 |
| 4 | 86 177 | 0,116 | 0,230 | 0,684 | 0,155 | 0,253 |
| 5 | 85 674 | 0,121 | 0,240 | 0,679 | 0,161 | 0,260 |
| 6 | 85 116 | 0,127 | 0,256 | 0,704 | 0,157 | 0,257 |
| 7 | 84 750 | 0,131 | 0,260 | 0,725 | 0,155 | 0,255 |
| 8 | 84 464 | 0,133 | 0,260 | 0,680 | 0,167 | 0,269 |
| 9 | 84 133 | 0,137 | 0,270 | 0,699 | 0,166 | 0,269 |
| 10 | 83 924 | 0,139 | 0,270 | 0,725 | 0,161 | 0,264 |
| 11 | 83 827 | 0,140 | 0,270 | 0,733 | 0,160 | 0,263 |
| 12 | 83 721 | 0,141 | 0,276 | 0,714 | 0,166 | 0,269 |
| 13 | 83 647 | 0,142 | 0,280 | 0,729 | 0,163 | 0,266 |
| 14 | 83 587 | 0,142 | 0,280 | 0,729 | 0,163 | 0,267 |
| 15 | 83 506 | 0,143 | 0,280 | 0,734 | 0,162 | 0,266 |
| 16 | 83 474 | 0,144 | 0,280 | 0,737 | 0,162 | 0,266 |
| 17 | 83 453 | 0,144 | 0,280 | 0,743 | 0,161 | 0,265 |
| 18 | 83 431 | 0,144 | 0,280 | 0,738 | 0,162 | 0,266 |
| 19 | 83 418 | 0,144 | 0,280 | 0,741 | 0,162 | 0,265 |
| 20 | 83 409 | 0,144 | 0,280 | 0,743 | 0,161 | 0,265 |
| 21 | 83 405 | 0,144 | 0,280 | 0,745 | 0,161 | 0,265 |
| 1) De relatieve entropie staat ook wel bekend als de McFadden (1974) pseudo-R2-waarde en kan daarbij ook vergeleken worden met de gemiddelde R2. 2) We geven de gemiddelde R2 weer, omdat deze per groep in de kruisvalidatie wordt berekend zoals beschreven in Bijlage 4.1.2. 3) Voor het intercept model worden geen fitmaten (excl. de entropie) weergegeven, omdat deze geen informatieve waarde hebben in de vergelijking van de modellen met kenmerken. | ||||||
In de tabel zien we dat de entropie afneemt, naarmate het model uitgebreider wordt. Het meest uitgebreide model kan de beste schatting maken voor vsv. De relatieve entropie geeft de relatieve verbetering ten opzichte van het lege model weer. Deze fitmaat laat zien dat er niet meer veel verandert vanaf het model met zestien kenmerken en er nog geringe veranderingen zijn in de modellen vanaf tien kenmerken.
De recall-waarde ligt tussen de 0,50 en 0,75. In het model tot zeven kenmerken neemt de recall telkens toe, vanaf zeven kenmerken zien we wisselingen in de waarde van de recall. De recall blijft echter altijd rond de 0,70 schommelen, wat betekent dat het mbo-model 70 procent van de studenten die werkelijk vsv’er worden vaak als zodanig classificeert. De precision ligt rond de 0,15 en 0,17, wat relatief laag is voor een precision-waarde, maar ook wel volgens verwachting bij een model met een laag aandeel vsv’ers in de populatie (7,9% op het mbo, zie ook paragraaf 2.4). De achtergrondkenmerken voegen echter wel veel toe aan het model in vergelijking met een leeg model. Stel de achtergrondkenmerken worden niet meegenomen en iedereen zou als vsv’er geclassificeerd worden, dan zou de precision gelijk zijn aan het aandeel vsv’ers in de mbo populatie, dus 0,079. Een model met kenmerken laat daarom een vooruitgang zien in de precision. De F1 neemt de bovenstaande resultaten samen.
De gemiddelde McKelveyZavoina R2 over de kruisvalidaties ligt tussen de 0,09 en 0,28. Hierbij is er een toename te zien tot model dertien, waarna de waarde constant blijft. Volgens deze fitmaat heeft het opnemen van meer dan dertien kenmerken geen toegevoegde waarde voor de verklaringskracht van het model. Deze R2 variant moet wel met voorzichtigheid worden geïnterpreteerd en de grootte van het effect is daarbij ook context-afhankelijk. We gebruiken de R2 in de kruisvalidaties dan ook voornamelijk om modelvergelijkingen te maken.
4.5 Conclusie modelselectie
Op basis van de eerdere analyses is er een definitief voorkeursmodel voor het mbo gekozen. Het doel was om een eenvoudig, transparant en goed uit te leggen model te maken, met zo veel mogelijk verklaringskracht. Bij de keuze voor een voorkeursmodel spelen verschillende factoren een rol. Een belangrijke reden is de stabiliteit van het model tussen cohorten. Het is van belang om een generiek model te ontwikkelen, dat ook inzetbaar is in andere cohorten. De resultaten in dit hoofdstuk lieten zien dat het model bij meer dan twaalf kenmerken minder stabiel wordt. Bovendien lieten de modelfitmaten zien dat er vanaf twaalf kenmerken weinig toegevoegde waarde was wat betreft de verklaringskracht van het model. Ook figuur 4.3.1 toonde een afvlakkende daling in de BIC-waarde vanaf twaalf kenmerken. Deze redenen samen leiden tot de conclusie dat een model met twaalf kenmerken de voorkeur heeft. Indien een verdere versimpeling van het model door het ministerie van OCW gewenst is en in fase 2 vergelijkbare resultaten oplevert met het voorkeursmodel zou er in het vervolg ook nog gekozen kunnen worden voor een model met zeven kenmerken (ook wel het “back-up model” genoemd). Al laat dat model wel een geringe achteruitgang in verklaringskracht zien. De coëfficiënten en Odds Ratio’s (OR) behorende bij het model met zeven en twaalf kenmerken worden weergegeven in bijlage 5.
Met behulp van de gegevens in figuur 4.5.1 kan een voorbeeld gegeven worden van de toepassing van de odds ratio’s voor een fictieve student. Deze student heeft bepaalde kenmerken, zoals mbo-niveau en leeftijd van de student. Elke categorie waarin een student valt, heeft een odds ratio ten opzichte van de referentiecategorie. Door vervolgens deze met elkaar te vermenigvuldigen, komen we uit op de odds op vsv van de betreffende student. Zie paragraaf 2.7 voor een uitgebreidere uitleg van odds en odds ratio’s. Volgens de figuur is de kans op vsv voor die student 0,333 keer zo groot als de kans op geen vsv. Bij deze kansverhouding hoort een geschatte kans op vsv van 0,250. De kans dat een student met deze combinatie van achtergrondkenmerken vsv’er wordt is dus 25,0%.

Omdat het hoogst behaalde opleidingsniveau van de moeder terugkomt in het uiteindelijke model met twaalf kenmerken, is er opnieuw beoordeeld of multipele imputatie nodig was. Dit is onderzocht door de resultaten uit twee imputatieronden met elkaar te vergelijken. Daaruit bleek dat de resultaten van de imputatieronden stabiel waren, waardoor geen multipele imputatie nodig was. De resultaten uit de eerste imputatieronde zijn gebruikt in het uiteindelijke model.
4.6 Stap 4: Uitbreiding met multilevel-component
Studenten zijn geclusterd binnen RMC-regio’s. Om te onderzoeken hoe sterk deze clustering is en of hier in de analyses rekening mee gehouden dient te worden, hebben we een multilevel model geschat. In een model met alleen een random intercept op RMC-regio niveau (dus zonder kenmerken in het model) was de Median Odds Ratio (MOR) 1,19 (95% betrouwbaarheidsinterval (BI): 1,15-1,25). Dat wil zeggen dat wanneer een student verhuist van een RMC-regio met een lagere odds op vsv naar een RMC-regio met een hogere odds op vsv, de mediane odds op vsv 1,19 keer zo groot zijn. Aangezien de MOR een odds ratio is, kan hij ook direct vergeleken worden met de andere odds ratio’s van de variabelen in het model. In verhouding is dit effect van RMC-regio dusdanig klein, dat wij hebben besloten hier in de analyses geen rekening mee te houden. Aanvullend is wel nog onderzocht of deze MOR nog kleiner werd na het toevoegen van de twaalf geselecteerde verklarende variabelen, wat inderdaad het geval was.
In het validatiecohort vonden wij een MOR van eenzelfde grootte (1,21, 95% BI: 1,17-1,28).
Hoewel de gevonden clusteringseffecten klein zijn, zijn ze wel statistisch significant. Hierbij moet worden bedacht dat het bestand een groot aantal waarnemingen bevat waardoor de kans op statistisch significante resultaten wordt vergroot.
4.7 Extra analyses
Tot slot zijn er twee aanvullende analyses uitgevoerd. Ten eerste hebben we, om de resultaten van het model te valideren, ook een vergelijkbare analyse uitgevoerd op basis van DUO-data. Zoals beschreven in paragraaf 2.3 en 2.4 hanteert DUO een andere afbakening van de populatie en een andere definitie voor vsv dan het CBS. We willen deze data daarom vooral gebruiken om te zien of een model op basis van DUO-data vergelijkbare kenmerken selecteert als het model dat is geschat op de CBS-data. Hiervoor is dezelfde forward stepwise procedure toegepast.
In tabel 4.7.1 worden de resultaten vergeleken. Het model op basis van DUO-data komt uit op 22 kenmerken i.p.v. 21 kenmerken op basis van CBS-data. Hiervan zijn de eerste twaalf kenmerken hetzelfde, waarin wel wat verschillen zitten in de volgorde van de kenmerken. Na de twaalf kenmerken zijn ook veel kenmerken dezelfde, alleen weer in een andere positie. Wel zijn het herkomstland van de student en de migratieachtergrond van de moeder nieuw toegevoegd aan het model van DUO. Daarnaast ontbreken het herkomstland van de moeder en de acute gezondheidsproblemen juist weer in het DUO-model. Dat herkomstland en migratieachtergrond verschillend voorkomen, kan komen doordat beide kenmerken relevant zijn, maar ook veel inhoudelijke overlap hebben. De stepwise procedure selecteert dan vaak één van beide kenmerken.
In paragraaf 4.5 hebben we geconcludeerd dat het model met twaalf kenmerken het beste als eindmodel gebruikt kan worden. Ook onderstaande resultaten bevestigen dat het model stabiel blijft bij twaalf kenmerken. De resultaten op basis van de CBS-data kunnen dus als valide beschouwd worden.
| Volgorde | Kenmerken (CBS 2018/’19) | Kenmerken (DUO 2018/’19) |
|---|---|---|
| 1 | Mbo-niveau | Mbo-niveau |
| 2 | Leeftijd van de student | Leeftijd van de student |
| 3 | Ouderlijke structuur | Ouderlijke structuur |
| 4 | Verdachte van een misdrijf | Verdachte van een misdrijf |
| 5 | Geslacht | Problematische schulden |
| 6 | Hoogst behaalde opleidingsniveau moeder | Geslacht |
| 7 | Problematische schulden | Hoogst behaalde opleidingsniveau moeder |
| 8 | Leerweg | Welvaart |
| 9 | Onderwijsrichting volgens ISCED | Leerweg |
| 10 | Welvaart | Onderwijsrichting volgens ISCED |
| 11 | Psychosociale problemen student | Stedelijkheid van de buurt |
| 12 | Stedelijkheid van de buurt | Psychosociale problemen student |
| 13 | Hoogst behaalde opleidingsniveau vader | Herkomstland student |
| 14 | Niveau van vooropleiding | Hoogst behaalde opleidingsniveau vader |
| 15 | Herkomstland moeder | Verblijfsduur van moeder in Nederland |
| 16 | Langdurige gezondheidsproblemen | Langdurige gezondheidsproblemen |
| 17 | Wanbetaler ZVW premie (ouders) | Migratieachtergrond moeder |
| 18 | Verblijfsduur van moeder in Nederland | Wanbetaler ZVW premie (ouders) |
| 19 | Acute gezondheidsproblemen | Acute gezondheidsproblemen |
| 20 | Psychosociale problemen moeder | Migratieachtergrond vader |
| 21 | Migratieachtergrond moeder | Psychosociale problemen moeder |
| 22 | Niveau van vooropleiding | |
Daarnaast hebben we op basis van het eindmodel met twaalf kenmerken voor de totale populatie op het mbo een simpele aggregatie uitgevoerd van de geschatte kansen op vsv. Dit betekent dat de geschatte kansen van alle studenten in een bepaalde RMC-regio bij elkaar zijn opgeteld. Hiermee krijgen we al een eerste indicatie van de verschillen tussen het werkelijk en geschatte aantal vsv’ers en hoe dit tussen regio’s verschilt. In fase 2 van dit onderzoek zal deze aggregatie naar RMC-regio niveau uitvoerig onderzocht worden. Hierbij zullen ook verschillende keuzes door het ministerie van OCW gemaakt moeten worden.
Om een eerste indicatie te geven van de samenhang tussen het werkelijke en geschatte aantal vsv’ers per RMC-regio op het mbo, hebben we de Pearson correlatiecoëfficiënt uitgerekend. Deze geeft een sterke samenhang aan tussen het werkelijke en geschatte aantal vsv’ers met \( \rho \)= 0,995.
Omdat het aantal studenten verschillend is per RMC-regio, geven we in figuur 4.7.2 de resultaten relatief weer t.o.v. het totaal aantal studenten per RMC-regio. Dit totale aantal is gebaseerd op de populatiedefinitie van dit onderzoek, dus studenten zonder startkwalificatie. Daarbij is te zien dat er relatief meer spreiding is in de werkelijke percentages dan in de geschatte percentages. Daarnaast komt zowel onderschatting (onder de blauwe lijn) als overschatting (boven de blauwe lijn) voor bij de regio’s.
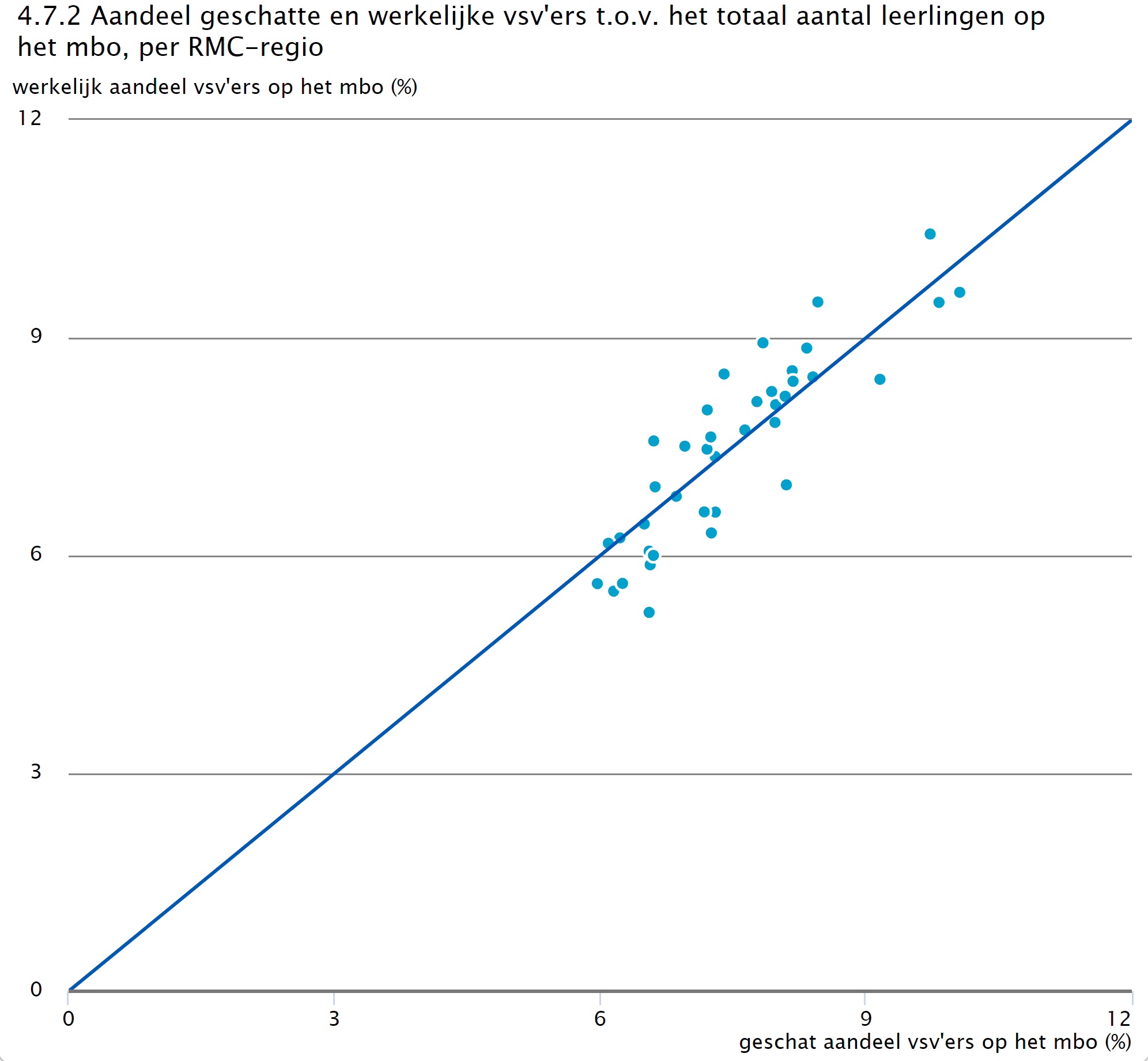
5. Samenvatting en conclusies
Het ministerie van OCW wil het financiële verdeelmodel voor voortijdig schoolverlaten (vsv) herzien. Het CBS heeft op verzoek van het ministerie van OCW verkend of het mogelijk is om, op basis van kenmerken die in registraties bij het CBS aanwezig zijn, een indicator te ontwikkelen om de omvang van de vsv-problematiek per regio te schatten. Het is voor het ministerie van OCW daarbij belangrijk dat de nieuwe indicator geen perverse prikkels kent en daarnaast transparant en duidelijk is, zodat regio’s begrijpen hoe het geld wordt verdeeld.
Het huidige rapport betreft de resultaten uit de eerste fase van het onderzoekstraject. Hierbij stond de vraag centraal of een model ontwikkeld kan worden om per leerling of student de kans op vsv te schatten. Daarbij werd onderzocht welke combinatie van kenmerken het beste hiervoor gebruikt kan worden. Eerder onderzoek liet al zien dat het daarbij belangrijk is om onderscheid te maken tussen het vo en het mbo. Op basis van suggesties van de begeleidingscommissie en eerdere onderzoeken van het CBS is vervolgens een lijst met mogelijke verklarende variabelen van vsv opgesteld. De basis van de uitgevoerde analyse vormde een zogenaamde stepwise-selectieprocedure, waarbij stap voor stap het kenmerk met de grootste verklaringskracht wordt toegevoegd aan het model, totdat het model niet of nauwelijks meer verbetert. Vervolgens zijn verschillende aanvullende analyses uitgevoerd om de kwaliteit en stabiliteit van de modellen te beoordelen. De resultaten hiervan zijn gebruikt om voor zowel het vo als het mbo een voorkeursmodel te selecteren.
Voor het vo bestaat het voorkeursmodel uit zeven kenmerken:
- leeftijd van de leerling;
- onderwijssoort;
- opgelopen vertraging;
- ouderlijke structuur;
- welvaartsniveau van het huishouden;
- of de leerling verdachte is geweest van een misdrijf; en
- de aanwezigheid van problematische schulden in het huishouden.
Het verder toevoegen van extra kenmerken leidde niet tot een duidelijk betere kwaliteit van het model en maakte daarnaast het model minder stabiel wanneer we dit vergeleken met een eerder cohort en data van DUO. Op basis van de validatie met deze cohorten en de resultaten van kruisvalidaties concluderen we dat dit voorkeursmodel een betrouwbare schatting geeft van de kans op vsv voor individuele leerlingen in het vo.
Het voorkeursmodel in het mbo bestaat uit meer kenmerken, namelijk twaalf:
- niveau van de mbo-opleiding;
- leeftijd van de student;
- ouderlijke structuur;
- of de student verdachte is geweest van een misdrijf;
- geslacht van de student;
- hoogst behaalde opleidingsniveau van de moeder;
- de aanwezigheid van problematische schulden;
- de gevolgde leerweg en onderwijsrichting;
- welvaartsniveau van het huishouden;
- of de student psychosociale problemen heeft; en
- de stedelijkheid van de buurt waar de student woont.
Het verder toevoegen van kenmerken leidde na het twaalfde kenmerk nauwelijks nog tot verbetering van het model. De validatie op basis van een eerder cohort en data van DUO liet zien dat dezelfde eerste twaalf kenmerken worden geselecteerd. Dit bevestigde de stabiliteit van het voorkeursmodel. Wij concluderen op basis van de kwaliteit en de stabiliteit dan ook dat het voorkeursmodel een betrouwbare schatting van de kans op vsv voor individuele studenten in het mbo geeft.
Verder is door middel van een multilevel analyse onderzocht of het nuttig is om bij de ontwikkeling van de modellen voor vsv rekening te houden met clustering van jongeren op schoolniveau (enkel voor vo) of op RMC-regioniveau (voor vo en mbo). Uit deze analyse bleek dat er relatief weinig clustering bestaat op RMC-regioniveau. Op schoolniveau is in het vo wel enige clustering aanwezig, maar deze kan grotendeels worden verklaard door de kenmerken uit het voorkeursmodel. De geschatte coëfficiënten uit het voorkeursmodel veranderden bovendien nauwelijks als een schooleffect werd toegevoegd. Onze conclusie is daarom dat uitbreiding van het voorkeursmodel voor vo en mbo met een multilevel-component niet of nauwelijks zou leiden tot betere schattingen van vsv op regionaal niveau.
Voor de totstandkoming van het model zijn kenmerken meegenomen die het CBS integraal (voor alle jongeren en hun ouders) tot zijn beschikking heeft vanwege zijn wettelijke taak. Het is mogelijk dat er andere kenmerken zijn, waarvoor de integrale gegevens momenteel niet bij het CBS aanwezig zijn, die mogelijk wel gerelateerd zijn aan de kans op vsv. Zoals eerder is genoemd laten de resultaten van de multilevel analyses echter zien dat er relatief weinig clustering is op RMC-regioniveau. Dat wil zeggen dat we waarschijnlijk geen kenmerken missen die op regioniveau van groot belang zijn.
Tot slot geven we een korte vooruitblik naar de tweede fase van dit onderzoekstraject. In deze fase zal een methode worden uitgewerkt om de geschatte kansen op individueel niveau te aggregeren naar een score per RMC-regio en zullen de gevolgen van de nieuwe verdeelsystematiek in kaart worden gebracht. Hierbij zullen aanvullende keuzes gemaakt moeten worden door het ministerie van OCW, bijvoorbeeld of er met bepaalde grenswaardes gewerkt zal worden, hoe in de uiteindelijke indicator onderscheid gemaakt zal worden tussen het vo en het mbo, en of een mogelijke verdere versimpeling van het voorkeursmodel tot een vergelijkbare verdeling van het budget leidt. In deze fase zullen diverse opties voor de aggregatie naar RMC-niveau met elkaar worden vergeleken en als input dienen voor het beslisproces van het ministerie van OCW. Het is aan het ministerie van OCW om op basis van deze resultaten af te wegen wat het meest gewenste beleidsalternatief is.
Bijlage 1: Begeleidingscommissie
Liesbeth de Boer – Ingrado
Doride de Bruin – MBO Raad
Duncan Bruyn van Rozenburg - DUO
Ton Eimers – KBA Nijmegen
Lex Herweijer – SCP
Paul Huisman – VO-Raad
Erwin Keuskamp – RMC-coördinator regio Zuid-Holland Zuid
Johan van der Lee – MBO Raad
Ans Pennartz – ROC Gilde
Petra Raaijen – VNG
Dennis Swart – ministerie van BZK
Nikki Slokkers – ministerie van BZK
Pierre Veelenturf – MBO Raad
Marga de Weerd – Ingrado
Bijlage 2: Databronnen
In dit onderzoek is gebruik gemaakt van gegevens uit het Stelsel van Sociaal-Statistische Bestanden (SSB) van het CBS. De bestanden die voor dit onderzoek uit het SSB gebruikt zijn, worden hieronder kort toegelicht.
Voortijdig schoolverlaters
In dit bestand zijn alle personen opgenomen die op 1 oktober van een schooljaar staan ingeschreven in het bekostigd voortgezet onderwijs (vo), middelbaar beroepsonderwijs (mbo) of voortgezet algemeen volwassenen onderwijs (vavo). Van deze personen is informatie beschikbaar over de opleiding die ze op dit moment volgen en over hun onderwijspositie een jaar later: uit onderwijs zonder startkwalificatie, door in onderwijs of uit onderwijs met startkwalificatie. Een startkwalificatie is een havo- of vwo-diploma of een diploma op ten minste mbo-niveau 2. Personen die het onderwijs verlaten zonder startkwalificatie worden voortijdig schoolverlaters (vsv'ers) genoemd.
Algemene onderwijsbestanden
Het CBS beschikt over gegevens over de kenmerken van leerlingen en studenten met 1 of meerdere inschrijvingen geldig op 1 oktober. Het betreft inschrijvingen in het bekostigd onderwijs, namelijk in het (speciaal) basisonderwijs (SBO), het (voortgezet) speciaal onderwijs ((V)SO), het voortgezet onderwijs (VO), het middelbaar beroepsonderwijs (MBO), het hoger onderwijs (HO), waaronder het hoger beroepsonderwijs (HBO) en wetenschappelijk onderwijs (WO), en de volwasseneneducatie (VE) in het betreffende school- danwel studiejaar. Het bestand bevat de kenmerken zoals het leerjaar in het vo en het type onderwijs van de huidige opleiding en het aantal jaren op het mbo.
Basisregistratie personen
De BRP bevat alle personen die vanaf 1 oktober 1994 voorkomen in de basisregistratie en bevat demografische achtergrondgegevens die niet of nauwelijks wijzigen, zoals de burgerlijke staat, de grootte van het huishouden, het land van herkomst, het geboortejaar en adresgegevens. Daarnaast maakt de BRP koppelingen mogelijk, zodat bijvoorbeeld samenwonende stellen of de ouders van kinderen kunnen worden geïdentificeerd. De BRP wordt beheerd door gemeenten.
Opleidingsniveaubestand
Deze bron bevat alleen records van personen waarvan de hoogst behaalde opleiding bekend is.
Deze informatie komt voor een deel van de personen uit verschillende registraties en voor een andere deel uit enquêteonderzoek dat is gebaseerd op steekproeven. Door het gebruik van meerdere jaargangen van bronnen is de dekkingsgraad over de jaren heen toegenomen, maar dit is nog niet volledig. Doordat onderwijsregistraties nog niet zo heel lang bestaan, ontbreekt registerinformatie over veel oudere Nederlanders. Ook particuliere opleidingen vallen buiten het bereik van de onderwijsregisters. Daarnaast is van veel personen die hun opleiding in het buitenland hebben gevolgd op dit moment (nog) onvoldoende betrouwbare registerinformatie beschikbaar. Dit betekent dat er voor het samenstellen van het Opleidingsniveaubestand een aanvullend beroep moet worden gedaan op gegevens uit enquêteonderzoek, waarvan de Enquête Beroepsbevolking (EBB) de belangrijkste is. Anders dan bij de onderwijsregistraties zijn de gegevens van de EBB alleen op steekproefbasis beschikbaar.
Inkomen van huishoudens en personen
De inkomensbestanden bevatten de jaarinkomens van huishoudens en personen en zijn voornamelijk gebaseerd op registers afkomstig van de Belastingdienst (fiscaal basisregister) en de bevolkingsregisters van gemeenten (BRP). Daarnaast worden gegevens verzameld uit de registraties van de studiefinanciering van de Dienst Uitvoering Onderwijs (DUO).
Vermogensbestand
Dit bestand bevat gegevens over de vermogens van huishoudens. De gegevens zijn afkomstig van onder andere de administratie van de Belastingdienst. Het betreft zowel aangifte- als aanslaggegevens van personen. Het vermogen wordt vastgesteld op het niveau van huishoudens.
Sociaaleconomische categorie
Deze component bevat gegevens over de sociaaleconomische categorie van personen. Meerdere bestanden met betrekking tot het maandelijks inkomen, zoals ontvanger van bijstand- AOW- of een studiebeurs, of iemand een zelfstandig ondernemer, werknemer of directeur is. Om de belangrijkste sociaaleconomische categorie te bepalen, worden alle inkomsten in de verslagmaand uit de verschillende inkomensbronnen die iemand heeft met elkaar vergeleken. Het hoogste bedrag is in principe bepalend voor de sociaaleconomische categorie. Daarnaast wordt meegenomen of een persoon ingeschreven staat bij een onderwijsinstelling.
Jeugdzorg
Data met betrekking tot jeugdhulp worden aan het CBS geleverd door de aanbieders ervan, in het kader van de Beleidsinformatie Jeugd. Het betreft hulp of zorg verleend in het kader van de Jeugdwet, uitgezonderd jeugdbescherming en jeugdreclassering en gaat om de volgende vormen: ambulante jeugdhulp op locatie v/d aanbieder, daghulp op locatie van de aanbieder, jeugdhulp in het netwerk van de jeugdige, met verblijf, pleegzorg, gezinsgericht en gesloten plaatsing. De bestanden worden door alle aanbieders van jeugdhulp aan het CBS geleverd.
Wanbetalers Zorgverzekeringswet
De registratie wanbetalers zorgverzekeringswet bevat informatie over het aantal wanbetalers in het kader van de Zorgverzekeringswet. Het gaat om personen van 18 jaar en ouder die ingeschreven staan in de BRP en een premieachterstand hebben van ten minste zes maanden. Personen bij wie sprake is van een stabilisatie-overeenkomst of die in een goed-betaler-regeling zitten, behoren niet tot de populatie. Het CAK levert de bestanden aan het CBS.
Schuldenproblematiek
Als onderdeel van het onderzoek Schuldenproblematiek in beeld (bekostigd door het ministerie van Sociale Zaken en Werkgelegenheid (SZW)) zijn geregistreerde problematische schulden in beeld gebracht. In deze microdatabestanden zijn voor de peilmomenten 1 januari 2018, 2019 en 2020 en 1 oktober 2020 geregistreerde problematische schulden op persoons- en huishoudniveau opgenomen. De populatie van de bestanden zijn alle personen die op het betreffende peilmoment stonden ingeschreven in de BRP.
HALT
Dit bestand bevat alle personen die in een bepaald jaar naar bureau HALT (Het ALTernatief) verwezen zijn. Daarnaast zijn er kenmerken beschikbaar over het type delict, de datum van delict en of de Halt-afdoening geslaagd is. De data worden door bureau HALT aan het CBS geleverd.
Registratie van verdachte van een misdrijf
Het CBS ontvangt een selectie uit de registraties van De Nationale Politie, de tien regionale eenheden en de Landelijke Eenheid via de landelijke bevragingsapplicatie BVI. Alle personen worden geregistreerd tegen wie een redelijk vermoeden van schuld van een misdrijf bestaat. Van alle personen is opgenomen hoe vaak en van welk misdrijf ze werden verdacht.
Zorgkosten
Dit bestand bevat alle Nederlandse ingezeten die verzekerd zijn via de basisverzekering en de kosten per persoon per zorgvorm. Het betreft alle gedeclareerde en goedgekeurde zorgkosten die vallen onder de basisverzekering van de Zorgverzekeringswet, inclusief het eigen risico. Kosten die worden vergoed vanuit de aanvullende verzekering en eigen bijdrage worden niet meegenomen. De kosten zijn onderverdeeld in zorgvormen, zoals huisartsenzorg, ziekenhuiszorg, revalidatiezorg enzovoort. Het CBS verkrijgt de data via Vektis, die de data van de zorgverzekeraars ontvangt.
Geneesmiddelenverstrekking
Dit bestand bevat alle geneesmiddelverstrekkingen die zijn vergoed aan personen die ingeschreven staan in de Basisregistratie Personen (BRP). Alle verstrekte medicijnen zijn gecodeerd volgens de ATC-classificatie, die is opgesteld door de World Health Organisation (WHO). De gegevens worden verzameld door de Risicovereveningsbestanden van het Zorginstituut Nederland.
Overzicht van alle postcodes met bijbehorende stedelijkheidscategorie en omgevingsadressendichtheid
Het Geografisch Basisregister bevat alle adressen van Nederland die zijn voorzien van een postcode, gemeentecode en wijk- en buurtcode. Dit wordt gebruikt om de omgevingsadressendichtheid (OAD) van buurten, wijken en gemeenten te bepalen. Dit wordt gedaan door het gemiddeld aantal adressen per vierkante kilometer binnen een cirkel met een straal van één kilometer op 1 januari. De OAD beoogt de mate van concentratie van menselijke activiteiten (wonen, werken, schoolgaan, winkelen, uitgaan etc.) weer te geven. Het CBS gebruikt de OAD om de stedelijkheid van een bepaald gebied te bepalen. Voor de berekening hiervan wordt eerst voor ieder adres de OAD vastgesteld. Daarna is het gemiddelde berekend van de omgevingsadressendichtheden van alle afzonderlijke adressen binnen het beschouwde gebied.
Bijlage 3: Operationalisering van de kenmerken
Deze bijlage bespreekt de operationalisering van de gebruikte kenmerken in dit onderzoek.
Voortijdig schoolverlaten
Voortijdig schoolverlaters zijn jongeren die op 1 oktober van het schooljaar (t0) ingeschreven zijn in het bekostigd vo, mbo of vavo en op 1 oktober één jaar later (t1) niet meer ingeschreven zijn in het onderwijs, geen startkwalificatie hebben én jonger zijn dan 27 jaar.
0 – Geen voortijdig schoolverlater op t1
1 – Wel een voortijdig schoolverlater op t1
Sociaal-demografische kenmerken
Leeftijd
De leeftijd van de leerling of student op 30 september in jaar t0 (in jaren) zoals geregistreerd in de BRP. Voor het vo geldt dat leeftijd tot en met 14 jaar samengevoegd is tot één categorie evenals leeftijd vanaf 19 jaar. De tussenliggende jaren zijn aparte categorieën. Voor het mbo geldt dat de leeftijd tot en met 16 jaar samengevoegd is tot één categorie. De andere jaren zijn hier aparte categorieën.
Geslacht
Geslacht van de leerling of student zoals geregistreerd in de BRP op 30 september in jaar t0.
1 - Man
2 - Vrouw
Herkomstland (leerling, student en ouders)
Het land van herkomst zoals geregistreerd in de BRP op 30 september in jaar t0. In 2022 is het CBS overgegaan op een nieuwe herkomstindeling. Deze indeling is met terugwerkende kracht toegepast op eerdere jaren. Herkomstland bestaat uit de volgende categorieën:
01 - Nederland
02 - Europa (exclusief Nederland)
03 - Turkije
04 - Marokko
05 - Suriname
06 - Nederlands-Caribisch gebied
07 - Indonesië
08 - Overig Afrika
09 - Overig Azië
10 - Overig Amerika en Oceanië
Migratieachtergrond (leerling, student en ouders)
Migratieachtergrond zoals geregistreerd in de BRP op 30 september in jaar t0. Dit is een combinatie van het geboorteland van de persoon zelf en van de ouders. De migratieachtergrond van de leerling en student wordt onderverdeeld in:
0 - Geboren in het buitenland
1 - Geboren in Nederland
2 - Geboren in Nederland, tenminste 1 ouder in het buitenland
De migratieachtergrond van de juridische ouders wordt onderverdeeld in:
0 - Geboren in het buitenland
1 - Geboren in Nederland
2 - Geboren in Nederland, tenminste 1 ouder in het buitenland
9 - Onbekend
Verblijfsduur (leerling, student en ouders)
Het aantal jaren dat de leerling, de student en de juridische ouders op 30 september in jaar t0 in Nederland verblijven is ingedeeld in drie categorieën:
1 - 0 t/m 5 jaar
2 - 5 t/m 10 jaar
3 - Langer dan 10 jaar
Ouderlijke structuur
Op basis van de BRP is in kaart gebracht of de juridische ouders op 30 september in jaar t0 in het zelfde huishouden wonen als de leerling of student.
1- Woont bij beide juridische ouders
2- Woont bij één van de juridische ouders (eventueel met partner)
3- Woont zonder juridische ouders
Ouder niet bekend
Eén of beide juridische ouders zijn op 30 september in jaar t0 niet bekend. Dit is opgedeeld in de volgende categorieën:
0 – Beide juridische ouders zijn bekend
1 – Minstens 1 juridische ouder is niet bekend
Hoogst behaalde opleidingsniveau (ouders)
Afkomstig uit het opleidingsniveaubestand voor iedereen die een geregistreerd (DUO/UWV) diploma heeft behaald of waarvan dit bekend is uit de Enquête Beroepsbevolking (EBB). Het opleidingniveau in jaar t0 is volgens de ISCED (International Standard Classification of Education) indeling gecategoriseerd in:
1. Laag
a. Basisonderwijs
b. Praktijkonderwijs, vmbo-b/k, mbo entreeopleiding
c. Vmbo-g/t, havo-, vwo-onderbouw
2. Midden
a. Mbo niveau 2 en 3
b. Mbo niveau 4
c. Havo-, vwo-bovenbouw
3. Hoog
a. Hbo-, wo-bachelor
b. Hbo-, wo-master, doctor
Het opleidingsniveau is niet voor iedereen bekend. Ontbrekende waarden zijn daarom geïmputeerd met behulp van achtergrondkenmerken. In paragraaf 2.6 is dit imputatieproces beschreven.
Welvaart
De financiële welvaart van een huishouden in jaar t0 is gebaseerd op zowel het gestandaardiseerd inkomen als het vermogen. De inkomens- en vermogensstatistiek zijn afkomstig van onder andere de administraties van de Belastingdienst. Na rangschikking op basis van het inkomen en vermogen is de financiële welvaart van een huishouden bepaald uit de som van het cumulatieve aandeel in het totale inkomen en het cumulatieve aandeel in het totale vermogen. Op grond van de optelling zijn de huishoudens vervolgens gerangschikt van laag naar hoog en in 100 groepen van gelijke omvang verdeeld. De eerste groep bevat dan de 1 procent huishoudens met de laagste financiële welvaart, de honderste groep bevat de 1 procent huishoudens met de hoogste financiële welvaart.
Institutionele huishoudens en particuliere huishoudens waarvan het inkomen/vermogen onbekend is, zijn niet in de percentielverdeling meegenomen (geen doelpopulatie). Voor het huidige onderzoek zijn de welvaartspercentielen ingedeeld in 6 categorieën:
1 - 1 t/m 20
2 - 21 t/m 40
3 - 41 t/m 60
4 - 61 t/m 80
5 - 81 t/m 100
9 – Onbekend
Huishoudinkomen onder de lage inkomensgrens
Om te bepalen of een huishouden een laag inkomen heeft, wordt het besteedbaar inkomen van het huishouden (exclusief gebonden overdrachten zoals huurtoeslag) omgerekend tot het gestandaardiseerde inkomen. Vervolgens wordt dit gestandaardiseerde inkomen (met het prijsindexcijfer voor de gezinsconsumptie) herleid naar het prijspeil in 2000. Het resulterende gestandaardiseerde en gedefleerde inkomen is laag wanneer het minder is dan 9.249 euro. Deze grens komt ongeveer overeen met de koopkracht van een bijstandsuitkering voor een alleenstaande in 1979, toen deze op zijn hoogst was.
0 - Huishoudinkomen op of boven lage inkomensgrens in jaar t0
1 - Huishoudinkomen onder lage inkomensgrens in jaar t0
Aantal gewerkte uren
Bij de bepaling van de deeltijdfactor (DTF) is uitgegaan van de deeltijdfactoren van banen medio oktober in jaar t0. Wanneer iemand op dat moment meerdere banen had, zijn de deeltijdfactoren van deze banen opgeteld. Deze variabele is alleen bepaald voor leerlingen van het vo, omdat werken bij mbo vaak onderdeel van de opleiding is.
0 - Jongere werkt niet
1 - DTF 0,3 of lager
2 - DTF hoger dan 0,3
Aanwezigheid van problemen
Psychosociale problemen (leerling, student en ouders)
Om psychosociale problemen te meten worden twee verschillende databronnen gebruikt. Er wordt hier onderscheid gemaakt tussen jeugdhulp voor personen jonger dan 18 jaar en GGZ-kosten voor personen vanaf 18 jaar en ouder.
Voor de data met betrekking tot jeugdhulp wordt gebruik gemaakt van de volgende bestanden: de registratie van de Provinciale jeugdzorg, de registratie van JeugdzorgPlus en de registratie van jeugdhulp in het kader van de Beleidsinformatie Jeugd. Jeugdhulp zonder verblijf uitgevoerd door het wijk- of buurtteam is niet meegenomen in onze definitie.
Voor leerlingen of studenten vanaf 18 jaar en voor de juridische ouders wordt gekeken naar kosten voor basis GGZ-zorg of kosten voor specialistische GGZ-zorg in het verslagjaar. Hiervoor maken wij gebruik van het bestand met de Zvw-zorgkosten afkomstig van Vektis. Omdat deze data op t0 niet op tijd beschikbaar zijn, worden de data van een peilmoment eerder gebruikt.
0 – Persoon heeft geen jeugdhulp (in jaar t0) of GGZ-kosten (in jaar t-1) gehad
1 – Persoon heeft wel jeugdhulp (in jaar t0) of GGZ-kosten (in jaar t-1) gehad
Langdurige gezondheidsproblemen
Langdurige gezondheidsproblemen worden gemeten door te kijken naar veelvuldig medicijngebruik. Door de World Health Organisation (WHO) worden geneesmiddelengroepen ingedeeld volgens de ATC-codering, waarbij ATC staat voor Anatomisch, Therapeutisch, Chemisch. Dit classificatiesysteem bestaat uit 7 posities, waarvan de eerste 4 in de geneesmiddelencomponent zijn opgenomen. Op basis van deze 4 posities ATC-code zijn in theorie 268 ATC4-geneesmiddelengroepen mogelijk, inclusief de groep 'niet ingevuld'. Wij hebben een onderscheid gemaakt tussen personen die medicijnen gebruiken uit minder dan vier ATC4-groepen en personen die medicijnen gebruiken uit vier of meer ATC4-groepen.
0 - Persoon gebruikt medicijnen uit minder dan vier ATC4-hoofdgroepen in jaar t0
1 - Persoon gebruikt medicijnen uit tenminste vier ATC4-hoofdgroepen in jaar t0
Acute gezondheidsproblemen
Acute gezondheidsproblemen zijn gemeten door te kijken naar hoge ziekenhuiskosten. Voor het bepalen van hoge kosten hebben wij jaarlijks de personen met de top 5 procent hoogste ziekenhuiskosten van Nederland (apart berekend voor vo en mbo) genomen voor de leeftijdsgroep 12-27 jaar en bekeken wie van onze populatie daartoe behoort. De top 5 procent komt ongeveer neer op personen met ziekenhuiskosten van meer dan 1500 euro per jaar. Het gaat om de jaarlijkse kosten van ziekenhuiszorg die verzekerd is via de basisverzekering (wettelijk verplicht via de Zorgverzekeringswet (Zvw) voor vrijwel alle Nederlandse ingezetenen); de kosten die daadwerkelijk vergoed zijn door de zorgverzekeraars, incl. de kosten die vanwege het eigen risico uiteindelijk door de verzekerden zelf zijn betaald maar excl. eigen betalingen. Hiervoor maken wij gebruik van het bestand met de Zvw-zorgkosten afkomstig van Vektis.
Omdat deze data op t0 niet op tijd beschikbaar zijn, worden de data van een peilmoment eerder gebruikt.
0 – Persoon heeft geen hoge ziekenhuiskosten in jaar t-1
1 – Persoon heeft hoge ziekenhuiskosten in jaar t-1
Verdachte van een misdrijf
Verdachten (redelijk vermoeden van schuld) van geregistreerde misdrijven die in een bepaald jaar voorkomen in het registratiesysteem BVI van de Nationale Politie. Er wordt geen onderscheid gemaakt naar type misdrijf. Hiervoor gebruiken wij het bronbestand met verdachten van de Politie.
0 – Niet verdacht geweest van een misdrijf in jaar t0
1 – Wel verdacht geweest van een misdrijf in jaar t0
Wanbetaler ZVW premie (ouders)
Om te bepalen of juridische ouders wanbetalers zijn van de ZVW premie, is nagegaan of zij op 31 december van het betreffende jaar bij CAK geregistreerd staan als wanbetaler.
0 – Ouders zijn geen wanbetaler van ZVW in jaar t0
1 – Minimaal één ouder is wanbetaler van ZVW in jaar t0
Problematische schulden
Er is sprake van problematische schulden als een persoon voldoet aan ten minste één van de volgende criteria op het peilmoment:
- Volgt een Wet Schuldsanering Natuurlijke Personen (WSNP)-traject;
- Heeft ten minste zes maanden de zorgpremie niet betaald;
- Een betalingsachterstand van een Wet Mulder-boete bij het Centraal Justitieel Incassobureau (CJIB) heeft waarvan de tweede aanmaning ten minste twee maanden openstaat, of zich al in een ernstigere wanbetalersfase bevindt. Daarnaast moet het openstaande bedrag in totaal minimaal 50 euro zijn;
- Heeft langer dan 27 maanden een toeslagschuld van totaal minimaal 50 euro openstaan bij de Belastingdienst;
- Heeft langer dan 15 maanden een schuld van totaal minimaal 50 euro voor overige belastingaanslagen openstaan bij de Belastingdienst;
- Heeft een belastingschuld die in de 12 maanden voor het peilmoment oninbaar is geleden;
- Heeft een betalingsachterstand bij de DUO van 3 maanden of langer en van minimaal 270 euro.
Bovenstaande definitie is ook wel de ‘smalle definitie’ van problematische schulden, omdat in tegenstelling tot de volledige definitie de volgende voorwaarden niet zijn meegenomen:
- Volgt een bij BKR geregistreerd minnelijk traject;
- Heeft een bij BKR geregistreerde betalingsachterstand;
- Is in het Centraal Curatele en Bewindsregister (CCBR) opgenomen op grond van verkwisting en/of problematische schulden.
In het huidige onderzoek maken we onderscheid tussen schulden op persoons- en huishoudensniveau. Voor leerlingen op het voortgezet onderwijs kijken we alleen naar de schulden op huishoudensniveau, omdat de leerlingen te jong zijn om persoonlijke schulden te hebben en vaak onder de 18 jaar zijn. Op het mbo wordt er eerst gekeken of er persoonlijke schulden zijn. Is dat niet het geval, dan kijken we of iemand schulden in het huishouden heeft.
Categorieën voor het vo:
0 - Geen problematische schulden in jaar t0
1 - Problematische schulden in het huishouden in jaar t0
Categorieën voor het mbo:
0 - Geen problematische schulden in jaar t0
1 - Problematische schulden in het huishouden in jaar t0
2 - Problematische schulden op persoonsniveau in jaar t0
Omgevingskenmerken
Stedelijkheid van de buurt
Op basis van de BRP is bekend in welke gemeente en buurt een leerling of student woont. Op basis van de omgevingsadressendichtheid wordt de mate van stedelijkheid bepaald. Hierbij wordt een standaardindeling in 5 categorieën gebruikt:
1 - Zeer sterk (meer dan 2500 omgevingsadressen/km2)
2 - Sterk (1500 tot 2500 omgevingsadressen/km2)
3 - Matig (1000 tot 1500 omgevingsadressen/km2)
4 - Weinig (500 tot 1000 omgevingsadressen/km2)
5 - Niet (minder 500 omgevingsadressen/km2)
Lage welvaart in de buurt
Zie operationalisering van ‘Welvaart’. Om welvaart op buurtniveau te bepalen is het aantal mensen met een lage welvaart (laagste 20%) opgeteld per buurt en gedeeld door het buurttotaal van de populatie.
Jeugdwerkloosheid
Jeugdwerkloosheidspercentage (populatie 15 tot 25 jaar) op gemeenteniveau in jaar t0. Gebaseerd op de tabel Arbeidsdeelname; regionale indeling van Statline.
Onderwijsgerelateerde kenmerken voor het vo:
Onderwijssoort
Dit is een samengesteld kenmerk op basis van het onderwijssoort en het leerjaar van de leerling. Voor het vmbo is ook onderscheid gemaakt tussen de verschillende leerwegen.
00 - Leerjaar 1 en 2
05 - Vmbo-basisberoeps leerjaar 3 + 4
06 - Vmbo-kaderberoeps leerjaar 3 + 4
07 - Vmbo-gemengd leerjaar 3 + 4
08 - Vmbo-theoretisch leerjaar 3 + 4
09 - Havo leerjaar 3 – 5 en algemeen leerjaar 3
10 - Vwo leerjaar 3 – 6
11 – Vavo
In het databestand van DUO is een afwijkende operationalisering gehanteerd, te weten:
0 - Leerjaar 1 en 2
2 - Vmbo leerjaar 3 + 4
3 - Havo leerjaar 3 - 5 en algemeen leerjaar 3
4 - Vwo leerjaar 3 - 6
5 - Vavo
Vertraging
Om vast te stellen of er vertraging is in de schoolcarriere, is gekeken of de leeftijd van de leerling gelijk is aan de gemiddelde leeftijd in het betreffende leerjaar (= leerjaar + 11 jaar). Het aantal jaar dat de leerling ouder is dan deze gemiddelde leeftijd, wordt gezien als het aantal jaar opgelopen vertraging. Voor vavo-leerlingen kan vertraging niet berekend worden.
0 - Geen vertraging
1 - 1 jaar vertraging
2 - Tenminste 2 jaar vertraging
9 - Vavo leerling
Ongeoorloofd verzuim
Om ongeoorloofd verzuim binnen het vo te bepalen, is gekeken of een leerling verwezen is naar Bureau Halt voor overtreding van de leerplichtwet.
0 - Geen overtreding van de leerplichtwet in jaar t0
1 - Overtreding van de leerplichtwet in jaar t0
Onderwijsgerelateerde kenmerken voor het mbo:
Niveau
Niveau van de mbo-opleiding:
1 - Entreeopleiding
2 - Niveau 2 (Basisberoepsopleiding)
3 - Niveau 3 (Vakopleiding)
4 - Niveau 4 (Middenkader-/specialistenopleiding)
Leerweg
In het mbo kunnen twee leerwegen onderscheiden worden:
- Beroepsopleidende leerweg (BOL);
- Beroepsbegeleidende leerweg (BBL).
Bij de BOL nemen stages tussen de 20 en 60 procent van de totale opleidingsduur in, terwijl dit bij de BBL meer dan 60 procent is. Daarnaast is er een groep die uitsluitend examen doet, maar van wie de leerweg onbekend is omdat zij in het examenjaar niet als deelnemers staan ingeschreven. Zij worden extranei genoemd.
20 - BOL (voltijd)
22 - BBL
23 - Extranei
Studierichting (ISCED indeling)
Op basis van de ISCED (International Standard Classification of Education) classificeringen, is de volgende indeling in studierichtingen gemaakt:
01 - Overige richtingen
03 - Zorg en maatschappij
04 - Economisch en juridisch
05 - Technisch
08 - Landbouw, diergeneeskunde en -verzorging
99 - Onbekend
Niveau van vooropleiding
Om het niveau van de gevolgde vooropleiding te bepalen is gekeken naar de hoogst behaalde opleiding tot nu toe. Hiervoor is gebruik gemaakt van het opleidingsniveaubestand voor iedereen die een geregistreerd (DUO/UWV) diploma heeft behaald of waarvan dit bekend is uit de Enquête Beroepsbevolking (EBB). Op basis hiervan is bepaald wat de hoogstbehaalde opleiding (tot nu toe) van de student is.
Hierbij wordt onderscheid gemaakt tussen:
111 - Basisonderwijs
121 - Praktijkonderwijs, vmbo-b/k, mbo entreeopleiding
122 - Vmbo-g/t, havo-/vwo-onderbouw
Clustervariabelen in het multilevel model
RMC-regio
De regionale aanpak voortijdig schoolverlaten in Nederland is verdeeld in verschillende Regionaal Meld- en Coördinatiepunt (RMC)-regio’s. Aan de hand van de woonplaats wordt een persoon ingedeeld in zo’n RMC-regio. In totaal zijn er 39 RMC-regio’s.
Instellingsnummer
Elke onderwijsinstelling heeft een eigen nummer, een BRIN-nummer, om geïdentificeerd te kunnen worden.
Bijlage 4: Onderzoeksmethoden
Deze bijlage beschrijft aanvullende informatie over de gebruikte methodes in dit onderzoek en geeft met name achtergrondinformatie bij de aanpak zoals bespreken in paragraaf 2.7.
B4.1 Logistische regressie
B4.1.1 Het model
Voor jongere \( i \) in de populatie op 1 oktober van jaar t0 noteren we de doelvariabele als \( y_i = 1 \) wanneer de jongere vsv’er is op 1 oktober van jaar t1 en anders \( y_i = 0 \). Verder noteren we de kans dat jongere \( i \) vsv’er is op die datum als \( p_i = P(y_i = 1) \). Deze kans kan worden gemodelleerd als functie van achtergrondkenmerken via logistische regressie.
De algemene vorm van dit model is (Agresti, 2013, pp. 119-120):
\[ \ln \left( \frac{p_i}{1 - p_i} \right) = \beta_0 + \sum_{k=1}^{K} \beta_k x_{ki}, \]
waarbij \( x_{1i}, \ldots, x_{ki}, \ldots, x_{Ki} \) de waarden van jongere \( i \) zijn op de achtergrondkenmerken die zijn opgenomen in het model. De regressiecoëfficiënten \( \beta_0, \beta_1, \ldots, \beta_K \) beschrijven het verband tussen de achtergrondkenmerken en de kans om vsv’er te worden. In de meest eenvoudige variant bevat het model geen achtergrondkenmerken en blijft alleen de constante term \( \beta_0 \) over.
Uit het logistische regressiemodel volgt de volgende formule voor de kans om vsv’er te worden:
\[ p_i = \frac{ \exp (\beta_0 + \sum_{k=1}^{K} \beta_k x_{ki}) }{1 + \exp (\beta_0 + \sum_{k=1}^{K} \beta_k x_{ki}) }. \]
Nadat de regressiecoëfficiënten zijn geschat, zeg door \( \hat{\beta}_0, \hat{\beta}_1, \ldots, \hat{\beta}_K \), kan met deze formule een geschatte kans worden berekend om vsv’er te worden (\( \hat{p}_i \)) voor elke jongere in de populatie.
Voor de interpretatie van de coëfficiënt \( \beta_k \) is het handig om te kijken naar het bijbehorende effect op de zogenaamde kansverhouding (odds):
\[ \frac{p_i}{1 - p_i} = \exp \left( \beta_0 + \sum_{k=1}^{K} \beta_k x_{ki} \right) = \exp (\beta_0) \prod_{k=1}^{K} [\exp (\beta_k)]^{x_{ki}}. \]
De factoren \( \exp (\beta_k) \) in dit product worden ook wel odds ratio’s genoemd. In dit onderzoek werken we uitsluitend met categoriale achtergrondkenmerken, waarbij elke categorie apart is gecodeerd als \( x_{ki} \in \left\{ 0,1 \right\} \). Bij elk kenmerk wordt dan een van de categorieën aangewezen als referentiecategorie, met als bijbehorende coëfficiënt \( \beta_k = 0 \) [en dus als odds ratio \( \exp (\beta_k) = 1 \)]. Voor alle andere categorieën beschrijven de factoren \( \exp (\beta_k) \) de verwachte toename [als \( \beta_k > 0 \) en dus \( \exp (\beta_k) > 1 \)] of afname [als \( \beta_k < 0 \) en dus \( \exp (\beta_k) < 1 \)] van de kansverhouding om vsv’er te worden ten opzichte van de gekozen referentiecategorie, rekening houdend met alle andere kenmerken die zijn opgenomen in het model.
B4.1.2 Fitmaten voor logistische regressie
Schattingen voor de coëfficiënten van het logistische regressiemodel worden bepaald door de natuurlijke logaritme van de likelihood-functie van het model te maximaliseren. Deze functie heeft de volgende vorm, waarbij de som loopt over alle \( n \) leerlingen of studenten in de data waarop het model geschat wordt:
\[ \ln L = \sum_{i=1}^{n} \left\{ y_i \ln p_i + (1 - y_i) \ln (1 - p_i) \right\}. \]
Voor een geschat model \( M \) is \( H(M) = - \ln \hat{L}(M) \) de waarde van deze functie, vermenigvuldigd met \( -1 \), als de geschatte kansen \( \hat{p}_i \) worden ingevuld in plaats van de werkelijke kansen \( p_i \). De functie \( H(M) \) wordt ook wel de kruisentropie van model \( M \) genoemd.
In dit onderzoek gebruiken we een aantal fitmaten om te vergelijken hoe goed verschillende logistische regressiemodellen (met verschillende selecties van achtergrondkenmerken) passen bij de data. Ten eerste wordt dit geëvalueerd via het Bayesiaanse Informatie-Criterium (BIC):
\[ \mathrm{BIC}(M) = ( \ln n ) ( K + 1 ) + 2 H(M). \]
Hierbij is \( K + 1\) het aantal te schatten regressiecoëfficiënten uit model \( M \). Een model past beter bij de data naarmate de BIC-waarde lager is. In dit criterium zit een afweging tussen enerzijds de wens om een model te vinden dat zo goed mogelijk bij de data past (dat wil zeggen een model met een zo laag mogelijke waarde van \( H(M) \)) en anderzijds de wens om het model zo eenvoudig mogelijk te houden (dat wil zeggen een model met een klein aantal parameters \( K + 1 \)).
Vervolgens wordt bij elk geschat model een pseudo-R2-waarde berekend. Bij een lineair regressiemodel is R2 een getal tussen 0 en 1 dat aangeeft welke fractie van de totale variantie van de doelvariabele wordt verklaard door de achtergrondkenmerken in het model. Voor een logistisch regressiemodel bestaat geen maat die exact equivalent is aan R2, maar er bestaan wel diverse pseudo-R2-waarden met een enigszins vergelijkbare interpretatie. Hier gebruiken we een variant die is voorgesteld door McKelvey & Zavoina (1975):
\[ R^{2}_{MZ} = \frac{ \frac{1}{n} \sum_{i=1}^{n} \left( \hat{\eta}_i - \bar{\hat{\eta}} \right)^2 }{ \frac{1}{n} \sum_{i=1}^{n} \left( \hat{\eta}_i - \bar{\hat{\eta}} \right)^2 + \pi^2 / 3 }. \]
Hierbij is \( \hat{\eta}_i = \hat{\beta}_0 + \sum_{k=1}^{K} \hat{\beta}_k x_{ki} \) de geschatte waarde voor jongere \( i \) op de logistische schaal en \( \bar{\hat{\eta}} = \sum_{i=1}^{n} \hat{\eta}_i / n \). Bij een ‘leeg’ model \( M_0 \) zonder achtergrondkenmerken is \( \hat{\eta}_i = \bar{\hat{\eta}} = \hat{\beta}_0 \) voor alle jongeren en dus \( R^{2}_{MZ} = 0 \), net als bij de gewone R2 voor een lineair regressiemodel.
Een laatste maat die we gebruiken om verschillende modellen te vergelijken is de relatieve (verbetering van de) kruisentropie van model \( M \) ten opzichte van het ‘lege’ model \( M_0 \):
\[ \Delta(M) = \frac{ H(M_0) - H(M) }{ H(M_0) } = 1 - \frac{ H(M) }{ H(M_0) }. \]
Dit is een evaluatiemaat die ligt tussen 0 en 1, waarbij 1 wijst op een ideaal schattend model en 0 op een model dat niet beter schat dan het ‘lege’ model. Deze relatieve kruisentropie staat ook wel bekend als de pseudo-R2-waarde van McFadden (1974) en kan daarbij ook vergeleken worden met andere pseudo-R2-waarden.
B4.1.3 Geschat vsv-gedrag voor individuele leerlingen of studenten
Uit een geschat model volgt voor elke jongere een geschatte kans op vsv, \( \hat{p}_i \). Hiermee kan voor elke jongere worden geschat of deze wel of niet vsv’er wordt, door een bepaalde grenswaarde \( 0 \leq \tau \leq 1 \) te kiezen en te definiëren: \( \hat{y}_i = 1 \) als \( \hat{p}_i \geq \tau \) en anders \( \hat{y}_i = 0 \). Hoewel het model niet gebruikt zal worden om voor individuele leerlingen of studenten te schatten of zij wel of niet vsv’er worden, zegt de kwaliteit van zulke schattingen wel iets over de mate waarin het model bij de data past. We bekijken daarom, naast de eerder genoemde fitmaten, ook een aantal bekende maten waarin het geschatte aantal vsv’ers wordt vergeleken met het werkelijke aantal vsv’ers.
Deze evaluatiematen zijn gebaseerd op de volgende kruistabel van het werkelijke en geschatte aantal vsv’ers:
| Geschat = 1 | Geschat = 0 | |
|---|---|---|
| Werkelijk = 1 | True Positives (TP) | False Negatives (FN) |
| Werkelijk = 0 | False Positives (FP) | True Negatives (TN) |
De recall voor vsv’ers is gedefinieerd als de verhouding TP / (TP + FN). Dit is de fractie van alle werkelijke vsv’ers die correct worden geschat door het model. De precision voor vsv’ers is gedefinieerd als de verhouding TP / (TP + FP). Dit is de fractie van alle geschatte vsv’ers door het model die ook in werkelijkheid vsv’er zijn. Ten slotte is de F1-score voor vsv’ers gelijk aan het harmonisch gemiddelde van recall en precision. Idealiter zou het model een hoge score moeten hebben op alle drie deze maten. In de praktijk heeft een model met een hogere recall vaak een lagere precision en vice versa.
Bij een gegeven model hangen de waarden van recall, precision en F1-score af van de gekozen grenswaarde \( \tau \). In dit onderzoek is de ‘optimale’ grenswaarde \( \tau \) voor elk model apart bepaald, door de som van de recall voor vsv’ers en de recall voor niet-vsv’ers te maximaliseren. Hierbij is de recall voor niet-vsv’ers gegeven door: TN / (TN + FP).
B4.2 Multilevel analyse
B4.2.1 Het model
In dit onderzoek is alleen gekeken naar uitbreidingen van het logistische regressiemodel met een clustereffect in de constante term (random intercept). Voor leerlingen in het vo zijn multilevel-modellen getest van de volgende vormen:
\[ \ln \left( \frac{p_{isr}}{1 - p_{isr}} \right) = \beta_0 + \sum_{k=1}^{K} \beta_k x_{kisr} + \beta_{01s}, \quad \beta_{01s} \sim N(0, \sigma^{2}_{S}) \]
\[ \ln \left( \frac{p_{isr}}{1 - p_{isr}} \right) = \beta_0 + \sum_{k=1}^{K} \beta_k x_{kisr} + \beta_{01r}, \quad \beta_{01r} \sim N(0, \sigma^{2}_{R}) \]
\[ \ln \left( \frac{p_{isr}}{1 - p_{isr}} \right) = \beta_0 + \sum_{k=1}^{K} \beta_k x_{kisr} + \beta_{01s} + \beta_{02r}, \quad \beta_{01s} \sim N(0, \sigma^{2}_{1S}), \beta_{02r} \sim N(0, \sigma^{2}_{2R}). \]
Hierbij is \( p_{isr} \) de kans om vsv’er te worden voor leerling \( i \) op school \( s \) binnen RMC-regio \( r \). De constante term \( \beta_{01s} \) verschilt per school, de constante termen \( \beta_{01r} \) en \( \beta_{02r} \) verschillen per regio. Een aanname van het multilevel-model is dat deze variërende constante termen gemiddeld nul zijn en mogen worden opgevat als trekkingen uit een normale verdeling. Het eerste model bevat een clustering op schoolniveau, het tweede model een clustering op regionaal niveau en het derde model bevat beide typen clustering naast elkaar.
De grootte van de variantie van de geclusterde constante termen (voor de bovenstaande modellen respectievelijk \( \sigma^{2}_{S} \), \( \sigma^{2}_{R} \) en \( \sigma^{2}_{1S} \) en \( \sigma^{2}_{2R} \)) geeft aan in hoeverre clustering op school- of regionaal niveau voorkomt in de data. Anders dan bij een lineair regressiemodel is het bij een logistisch regressiemodel lastig om de grootte van deze variantie direct te interpreteren. Om te evalueren in hoeverre clustering voorkomt in de data – en daarmee in hoeverre een multilevel-model hier toegevoegde waarde heeft boven een gewoon logistisch regressiemodel – kijken we in dit onderzoek daarom naar een afgeleide maat, het mediane effect van de clustering op de kansverhoudingen (median odds ratio; MOR). De interpretatie van de MOR is vergelijkbaar met die van de eerder genoemde odds ratio’s \( \exp (\beta_k) \); zie de volgende paragraaf voor meer details.
B4.2.2 Median Odds Ratio (MOR)
Conceptueel is de MOR als volgt gedefinieerd: stel, we doen een gedachtenexperiment waarbij twee willekeurige clusters (d.w.z. scholen of regio’s) worden gekozen. Bij de ene cluster hoort een lagere constante term dan bij de andere. Stel nu dat we een jongere uit de cluster met de lagere constante term verplaatsen naar de cluster met de hogere constante term. Hierdoor neemt de kansverhouding op vsv van deze jongere, \( p_i / (1 - p_i) \), toe met een bepaalde factor. De MOR is nu gelijk aan de mediaan van deze factor wanneer we dit gedachtenexperiment zouden herhalen voor alle mogelijke paren van clusters. De MOR is per definitie groter dan of gelijk aan 1. Een hogere MOR wijst op een grotere rol van clustering bij vsv.
In de praktijk kan de MOR worden berekend met de volgende formule (Merlo et al., 2006):
\[ \mathrm{MOR} = \exp \left( q_{0,75} \sqrt{2 \sigma^2} \right). \]
Hierbij is \( q_{0,75} \approx 0,6745 \) het 75%-kwantiel van de verdelingsfunctie van de standaardnormale verdeling. Voor \( \sigma^2 \) wordt de variantie van een geclusterde constante term ingevuld (dat wil zeggen: een van de varianties \( \sigma^{2}_{S} \), \( \sigma^{2}_{R} \), \( \sigma^{2}_{1S} \) en \( \sigma^{2}_{2R} \)).
Een 95%-betrouwbaarheidsinterval rond geschatte waarden van \( \sigma^2 \) en/of MOR kan in de praktijk worden bepaald met de zogenaamde profile likelihood-methode; zie bijvoorbeeld Agresti (2013, pp. 79-80).
Bijlage 5: Resultaten logistische regressieanalyses
| Uitkomst | Coëfficient | Standaardfout | Z-score | P-waarde | Odds ratio |
|---|---|---|---|---|---|
| Constante1) | -8,279 | 0,083 | -99,185 | <0,001 | 0,000 |
| Leeftijd | |||||
| referentiecategorie: t/m 14 jaar | |||||
| 15 jaar | 1,355 | 0,066 | 20,680 | <0,001 | 3,877 |
| 16 jaar | 2,167 | 0,071 | 30,419 | <0,001 | 8,734 |
| 17 jaar | 3,424 | 0,078 | 43,856 | <0,001 | 30,689 |
| 18 jaar | 3,606 | 0,088 | 41,099 | <0,001 | 36,822 |
| 19 t/m 26 jaar | 4,085 | 0,092 | 44,619 | <0,001 | 59,468 |
| Onderwijssoort | |||||
| referentiecategorie: vwo leerjaren 3 t/m 6 | |||||
| leerjaren 1 en 2 | 1,377 | 0,074 | 18,626 | <0,001 | 3,962 |
| vmbo-basisberoeps: leerjaren 3 en 4 | 1,808 | 0,070 | 25,887 | <0,001 | 6,100 |
| vmbo-kaderberoeps: leerjaren 3 en 4 | 1,534 | 0,069 | 22,292 | <0,001 | 4,638 |
| vmbo-gemengd: leerjaren 3 en 4 | 1,349 | 0,097 | 13,893 | <0,001 | 3,853 |
| vmbo-theoretisch: leerjaren 3 en 4 | 1,719 | 0,064 | 26,954 | <0,001 | 5,580 |
| havo: leerjaren 3 t/m 5 en algemeen leerjaar 3 | 0,257 | 0,055 | 4,631 | <0,001 | 1,293 |
| vavo | 2,736 | 0,060 | 45,724 | <0,001 | 15,432 |
| Vertraging | |||||
| referentiecategorie: geen vertraging | |||||
| 1 jaar vertraging | 0,389 | 0,046 | 8,524 | <0,001 | 1,475 |
| tenminste 2 jaar vertraging | 1,288 | 0,061 | 21,128 | <0,001 | 3,624 |
| Ouderlijke structuur | |||||
| referentiecategorie: woont bij beide ouders | |||||
| woont bij 1 van de ouders (evt. + partner) | 0,444 | 0,028 | 15,950 | <0,001 | 1,560 |
| woont zonder ouders | 0,762 | 0,050 | 15,148 | <0,001 | 2,143 |
| Welvaartspercentiel | |||||
| referentiecategorie: 1 t/m 20 | |||||
| 21 t/m 40 | -0,176 | 0,040 | -4,393 | <0,001 | 0,839 |
| 41 t/m 60 | -0,303 | 0,043 | -7,129 | <0,001 | 0,738 |
| 61 t/m 80 | -0,350 | 0,045 | -7,730 | <0,001 | 0,704 |
| 81 t/m 100 | 0,316 | 0,041 | 7,750 | <0,001 | 1,371 |
| onbekend | 0,202 | 0,055 | 3,671 | <0,001 | 1,224 |
| Verdachte van een misdrijf | |||||
| referentiecategorie: geen | |||||
| wel | 0,959 | 0,061 | 15,808 | <0,001 | 2,610 |
| Problematische schulden huishouden | |||||
| referentiecategorie: geen | |||||
| wel | 0,340 | 0,040 | 8,527 | <0,001 | 1,404 |
| 1) De OR van de constante komt uit op 0 vanwege de afronding op drie decimalen. De OR met meer decimalen kan verkregen worden door de exponent van de coëfficient te nemen. Dit geldt ook voor alle andere OR's. | |||||
| Uitkomst | Coëfficient | Standaardfout | Z-score | P-waarde | Odds ratio |
|---|---|---|---|---|---|
| Constante1) | -8,189 | 0,082 | -99,354 | <0,001 | 0,000 |
| Leeftijd | |||||
| referentiecategorie: t/m 14 jaar | |||||
| 15 jaar | 1,341 | 0,065 | 20,550 | <0,001 | 3,821 |
| 16 jaar | 2,149 | 0,071 | 30,338 | <0,001 | 8,579 |
| 17 jaar | 3,393 | 0,078 | 43,702 | <0,001 | 29,763 |
| 18 jaar | 3,552 | 0,087 | 40,731 | <0,001 | 34,885 |
| 19 t/m 26 jaar | 4,025 | 0,091 | 44,220 | <0,001 | 56,004 |
| Onderwijssoort | |||||
| referentiecategorie: vwo leerjaren 3 t/m 6 | |||||
| leerjaren 1 en 2 | 1,355 | 0,073 | 18,442 | <0,001 | 3,877 |
| vmbo-basisberoeps: leerjaren 3 en 4 | 1,877 | 0,069 | 27,041 | <0,001 | 6,532 |
| vmbo-kaderberoeps: leerjaren 3 en 4 | 1,566 | 0,069 | 22,841 | <0,001 | 4,789 |
| vmbo-gemengd: leerjaren 3 en 4 | 1,354 | 0,097 | 13,975 | <0,001 | 3,873 |
| vmbo-theoretisch: leerjaren 3 en 4 | 1,729 | 0,064 | 27,181 | <0,001 | 5,634 |
| havo: leerjaren 3 t/m 5 en algemeen leerjaar 3 | 0,250 | 0,055 | 4,519 | <0,001 | 1,284 |
| vavo | 2,792 | 0,060 | 46,796 | <0,001 | 16,318 |
| Vertraging | |||||
| referentiecategorie: geen vertraging | |||||
| 1 jaar vertraging | 0,410 | 0,046 | 9,001 | <0,001 | 1,507 |
| tenminste 2 jaar vertraging | 1,333 | 0,061 | 21,915 | <0,001 | 3,792 |
| Ouderlijke structuur | |||||
| referentiecategorie: woont bij beide ouders | |||||
| woont bij 1 van de ouders (evt. + partner) | 0,469 | 0,028 | 16,912 | <0,001 | 1,598 |
| woont zonder ouders | 0,759 | 0,050 | 15,174 | <0,001 | 2,137 |
| Welvaartspercentiel | |||||
| referentiecategorie: 1 t/m 20 | |||||
| 21 t/m 40 | -0,199 | 0,040 | -4,998 | <0,001 | 0,819 |
| 41 t/m 60 | -0,359 | 0,042 | -8,512 | <0,001 | 0,699 |
| 61 t/m 80 | -0,411 | 0,045 | -9,195 | <0,001 | 0,663 |
| 81 t/m 100 | 0,249 | 0,040 | 6,230 | <0,001 | 1,283 |
| onbekend | 0,159 | 0,055 | 2,919 | 0,004 | 1,173 |
| 1) De OR van de constante komt uit op 0 vanwege de afronding op drie decimalen. De OR met meer decimalen kan verkregen worden door de exponent van de coëfficient te nemen. Dit geldt ook voor alle andere OR's. | |||||
| Uitkomst | Coëfficient | Standaardfout | Z-score | P-waarde | Odds ratio |
|---|---|---|---|---|---|
| Constante1) | -8,370 | 0,082 | -101,992 | <0,001 | 0,000 |
| Leeftijd | |||||
| referentiecategorie: t/m 14 jaar | |||||
| 15 jaar | 1,494 | 0,063 | 23,700 | <0,001 | 4,454 |
| 16 jaar | 2,196 | 0,069 | 31,700 | <0,001 | 8,986 |
| 17 jaar | 3,437 | 0,076 | 45,464 | <0,001 | 31,082 |
| 18 jaar | 3,634 | 0,085 | 42,927 | <0,001 | 37,873 |
| 19 t/m 26 jaar | 4,155 | 0,090 | 46,234 | <0,001 | 63,750 |
| Onderwijssoort | |||||
| referentiecategorie: vwo leerjaren 3 t/m 6 | |||||
| leerjaren 1 en 2 | 1,593 | 0,072 | 22,045 | <0,001 | 4,919 |
| vmbo-basisberoeps: leerjaren 3 en 4 | 1,857 | 0,068 | 27,285 | <0,001 | 6,403 |
| vmbo-kaderberoeps: leerjaren 3 en 4 | 1,441 | 0,069 | 20,759 | <0,001 | 4,225 |
| vmbo-gemengd: leerjaren 3 en 4 | 1,511 | 0,092 | 16,433 | <0,001 | 4,533 |
| vmbo-theoretisch: leerjaren 3 en 4 | 1,669 | 0,064 | 26,199 | <0,001 | 5,309 |
| havo: leerjaren 3 t/m 5 en algemeen leerjaar 3 | 0,311 | 0,055 | 5,627 | <0,001 | 1,365 |
| vavo | 2,775 | 0,059 | 46,659 | <0,001 | 16,036 |
| Vertraging | |||||
| referentiecategorie: geen vertraging | |||||
| 1 jaar vertraging | 0,377 | 0,044 | 8,565 | <0,001 | 1,458 |
| tenminste 2 jaar vertraging | 1,223 | 0,059 | 20,610 | <0,001 | 3,397 |
| Ouderlijke structuur | |||||
| referentiecategorie: woont bij beide ouders | |||||
| woont bij 1 van de ouders (evt. + partner) | 0,421 | 0,028 | 15,217 | <0,001 | 1,524 |
| woont zonder ouders | 0,734 | 0,047 | 15,525 | <0,001 | 2,083 |
| Welvaartspercentiel | |||||
| referentiecategorie: 1 t/m 20 | |||||
| 21 t/m 40 | -0,184 | 0,040 | -4,607 | <0,001 | 0,832 |
| 41 t/m 60 | -0,297 | 0,042 | -7,095 | <0,001 | 0,743 |
| 61 t/m 80 | -0,290 | 0,044 | -6,555 | <0,001 | 0,748 |
| 81 t/m 100 | 0,380 | 0,040 | 9,406 | <0,001 | 1,462 |
| onbekend | 0,205 | 0,050 | 4,102 | <0,001 | 1,228 |
| Verdachte van een misdrijf | |||||
| referentiecategorie: geen | |||||
| wel | 0,829 | 0,058 | 14,396 | <0,001 | 2,291 |
| Problematische schulden huishouden | |||||
| referentiecategorie: geen | |||||
| wel | 0,482 | 0,038 | 12,735 | <0,001 | 1,619 |
| 1) De OR van de constante komt uit op 0 vanwege de afronding op drie decimalen. De OR met meer decimalen kan verkregen worden door de exponent van de coëfficient te nemen. Dit geldt ook voor alle andere OR's. | |||||
| Uitkomst | Coëfficient | Standaardfout | Z-score | P-waarde | Odds ratio |
|---|---|---|---|---|---|
| Constante1) | -9,498 | 0,105 | -90,497 | <0,001 | 0,000 |
| Leeftijd | |||||
| referentiecategorie: t/m 14 jaar | |||||
| 15 jaar | 1,428 | 0,083 | 17,144 | <0,001 | 4,172 |
| 16 jaar | 2,748 | 0,085 | 32,460 | <0,001 | 15,612 |
| 17 jaar | 4,606 | 0,086 | 53,683 | <0,001 | 100,072 |
| 18 jaar | 4,885 | 0,092 | 52,834 | <0,001 | 132,342 |
| 19 t/m 26 jaar | 5,293 | 0,096 | 54,893 | <0,001 | 198,859 |
| Onderwijssoort | |||||
| referentiecategorie: vwo | |||||
| brugklassen/algemene leerjaren | 2,419 | 0,088 | 27,336 | <0,001 | 11,236 |
| vmbo | 2,476 | 0,075 | 33,170 | <0,001 | 11,888 |
| havo | 0,807 | 0,073 | 11,115 | <0,001 | 2,241 |
| vavo | 2,324 | 0,071 | 32,530 | <0,001 | 10,221 |
| Ouderlijke structuur | |||||
| referentiecategorie: woont bij beide ouders | |||||
| woont bij 1 van de ouders (evt. + partner) | 0,510 | 0,034 | 15,089 | <0,001 | 1,666 |
| woont zonder ouders | 0,761 | 0,061 | 12,540 | <0,001 | 2,139 |
| onbekend | 1,898 | 0,172 | 11,037 | <0,001 | 6,675 |
| Verdachte van een misdrijf | |||||
| referentiecategorie: geen | |||||
| wel | 1,106 | 0,068 | 16,304 | <0,001 | 3,022 |
| Vertraging | |||||
| referentiecategorie: geen vertraging | |||||
| 1 jaar vertraging | -0,153 | 0,049 | -3,106 | 0,002 | 0,858 |
| tenminste 2 jaar vertraging | 0,491 | 0,052 | 9,414 | <0,001 | 1,633 |
| Problematische schulden huishouden | |||||
| referentiecategorie: geen | |||||
| wel | 0,439 | 0,045 | 9,692 | <0,001 | 1,552 |
| Welvaartspercentiel | |||||
| referentiecategorie: 1 t/m 20 | |||||
| 21 t/m 40 | -0,185 | 0,046 | -4,064 | <0,001 | 0,831 |
| 41 t/m 60 | -0,392 | 0,050 | -7,889 | <0,001 | 0,676 |
| 61 t/m 80 | -0,447 | 0,053 | -8,367 | <0,001 | 0,640 |
| 81 t/m 100 | -0,405 | 0,055 | -7,423 | <0,001 | 0,667 |
| onbekend | 0,205 | 0,067 | 3,053 | 0,002 | 1,227 |
| 1) De OR van de constante komt uit op 0 vanwege de afronding op drie decimalen. De OR met meer decimalen kan verkregen worden door de exponent van de coëfficient te nemen. Dit geldt ook voor alle andere OR's. | |||||
| Uitkomst | Coëfficient | Standaardfout | Z-score | P-waarde | Odds ratio |
|---|---|---|---|---|---|
| Constante | -4,638 | 0,046 | -100,335 | <0,001 | 0,010 |
| Niveau | |||||
| referentiecategorie: niveau 4 | |||||
| entreeopleiding | 1,802 | 0,027 | 66,767 | <0,001 | 6,063 |
| niveau 2 | 0,664 | 0,017 | 38,306 | <0,001 | 1,943 |
| niveau 3 | 0,208 | 0,020 | 10,382 | <0,001 | 1,231 |
| Leeftijd | |||||
| referentiecategorie: t/m 16 jaar | |||||
| 17 jaar | 1,708 | 0,034 | 50,722 | <0,001 | 5,517 |
| 18 jaar | 1,645 | 0,034 | 48,115 | <0,001 | 5,182 |
| 19 jaar | 1,684 | 0,036 | 47,149 | <0,001 | 5,387 |
| 20 jaar | 1,824 | 0,038 | 47,502 | <0,001 | 6,195 |
| 21 jaar | 1,998 | 0,042 | 47,186 | <0,001 | 7,371 |
| 22 jaar | 1,981 | 0,049 | 40,408 | <0,001 | 7,250 |
| 23 jaar | 1,969 | 0,055 | 35,637 | <0,001 | 7,164 |
| 24 jaar | 1,903 | 0,061 | 30,978 | <0,001 | 6,708 |
| 25 jaar | 1,844 | 0,068 | 27,079 | <0,001 | 6,323 |
| 26 jaar | 1,821 | 0,075 | 24,385 | <0,001 | 6,180 |
| Ouderlijke structuur | |||||
| referentiecategorie: woont bij beide ouders | |||||
| woont bij 1 van de ouders (evt. + partner) | 0,375 | 0,016 | 24,100 | <0,001 | 1,455 |
| woont zonder ouders | 0,612 | 0,024 | 25,700 | <0,001 | 1,845 |
| Verdachte van een misdrijf | |||||
| referentiecategorie: niet | |||||
| wel | 0,853 | 0,027 | 31,495 | <0,001 | 2,347 |
| Geslacht | |||||
| referentiecategorie: man | |||||
| vrouw | -0,532 | 0,015 | -34,343 | <0,001 | 0,587 |
| Hoogst behaalde opleidingsniveau moeder | |||||
| referentiecategorie: middelbaar | |||||
| laag | 0,222 | 0,015 | 14,516 | <0,001 | 1,249 |
| hoog | -0,105 | 0,021 | -5,009 | <0,001 | 0,900 |
| onbekend | -0,351 | 0,037 | -9,366 | <0,001 | 0,704 |
| Problematische schulden | |||||
| referentiecategorie: student en huishouden zonder schulden | |||||
| student met schulden | 0,625 | 0,037 | 16,892 | <0,001 | 1,868 |
| huishouden met schulden | 0,363 | 0,020 | 18,456 | <0,001 | 1,438 |
| Leerweg | |||||
| referentiecategorie: BOL | |||||
| BBL | 0,607 | 0,019 | 32,510 | <0,001 | 1,835 |
| extranei | 0,437 | 0,043 | 10,219 | <0,001 | 1,548 |
| Studierichting | |||||
| referentiecategorie: zorg en maatschappij | |||||
| economisch en juridisch | 0,101 | 0,023 | 4,316 | <0,001 | 1,106 |
| technisch | -0,376 | 0,027 | -13,916 | <0,001 | 0,687 |
| landbouw, diergeneeskunde en -verzorging | -0,025 | 0,042 | -0,607 | 0,544 | 0,975 |
| overige richtingen | 0,022 | 0,022 | 0,990 | 0,322 | 1,022 |
| onbekend | -0,216 | 0,055 | -3,913 | <0,001 | 0,805 |
| Welvaartspercentiel | |||||
| referentiecategorie: 1 t/m 20 | |||||
| 21 t/m 40 | -0,095 | 0,019 | -4,915 | <0,001 | 0,909 |
| 41 t/m 60 | -0,225 | 0,022 | -10,423 | <0,001 | 0,799 |
| 61 t/m 80 | -0,309 | 0,024 | -12,980 | <0,001 | 0,734 |
| 81 t/m 100 | -0,420 | 0,028 | -15,068 | <0,001 | 0,657 |
| onbekend | 0,053 | 0,036 | 1,469 | 0,142 | 1,054 |
| Psychosociale problemen student | |||||
| referentiecategorie: geen | |||||
| wel | 0,502 | 0,034 | 14,644 | <0,001 | 1,652 |
| Stedelijkheid van de buurt | |||||
| referentiecategorie: niet stedelijk | |||||
| zeer sterk stedelijk | 0,309 | 0,024 | 12,830 | <0,001 | 1,362 |
| sterk stedelijk | 0,265 | 0,023 | 11,501 | <0,001 | 1,303 |
| matig stedelijk | 0,183 | 0,024 | 7,466 | <0,001 | 1,200 |
| weinig stedelijk | 0,090 | 0,026 | 3,497 | <0,001 | 1,094 |
| Uitkomst | Coëfficient | Standaardfout | Z-score | P-waarde | Odds ratio |
|---|---|---|---|---|---|
| Constante | -4,759 | 0,034 | -138,309 | <0,001 | 0,009 |
| Niveau | |||||
| referentiecategorie: niveau 4 | |||||
| entreeopleiding | 1,938 | 0,024 | 79,452 | <0,001 | 6,945 |
| niveau 2 | 0,818 | 0,016 | 50,657 | <0,001 | 2,267 |
| niveau 3 | 0,308 | 0,019 | 16,106 | <0,001 | 1,360 |
| Leeftijd | |||||
| referentiecategorie: t/m 16 jaar | |||||
| 17 jaar | 1,711 | 0,034 | 50,979 | <0,001 | 5,537 |
| 18 jaar | 1,664 | 0,034 | 48,835 | <0,001 | 5,282 |
| 19 jaar | 1,753 | 0,035 | 49,409 | <0,001 | 5,773 |
| 20 jaar | 1,936 | 0,038 | 50,903 | <0,001 | 6,928 |
| 21 jaar | 2,143 | 0,042 | 51,106 | <0,001 | 8,524 |
| 22 jaar | 2,145 | 0,049 | 44,098 | <0,001 | 8,544 |
| 23 jaar | 2,155 | 0,055 | 39,295 | <0,001 | 8,628 |
| 24 jaar | 2,091 | 0,061 | 34,208 | <0,001 | 8,093 |
| 25 jaar | 2,038 | 0,068 | 30,124 | <0,001 | 7,674 |
| 26 jaar | 2,042 | 0,074 | 27,559 | <0,001 | 7,707 |
| Ouderlijke structuur | |||||
| referentiecategorie: woont bij beide ouders | |||||
| woont bij 1 van de ouders (evt. + partner) | 0,490 | 0,015 | 33,111 | <0,001 | 1,632 |
| woont zonder ouders | 0,812 | 0,022 | 36,739 | <0,001 | 2,253 |
| Verdachte van een misdrijf | |||||
| referentiecategorie: niet | |||||
| wel | 0,888 | 0,027 | 32,916 | <0,001 | 2,431 |
| Geslacht | |||||
| referentiecategorie: man | |||||
| vrouw | -0,495 | 0,014 | -35,312 | <0,001 | 0,610 |
| Hoogst behaalde opleidingsniveau moeder | |||||
| referentiecategorie: middelbaar | |||||
| laag | 0,289 | 0,015 | 19,550 | <0,001 | 1,335 |
| hoog | -0,130 | 0,021 | -6,267 | <0,001 | 0,878 |
| onbekend | -0,477 | 0,037 | -12,862 | <0,001 | 0,621 |
| Problematische schulden | |||||
| referentiecategorie: student en huishouden zonder schulden | |||||
| student met schulden | 0,670 | 0,037 | 18,187 | <0,001 | 1,954 |
| huishouden met schulden | 0,436 | 0,019 | 22,510 | <0,001 | 1,546 |
| Uitkomst | Coëfficient | Standaardfout | Z-score | P-waarde | Odds ratio |
|---|---|---|---|---|---|
| Constante | -4,989 | 0,051 | -97,731 | <0,001 | 0,007 |
| Niveau | |||||
| referentiecategorie: 4 | |||||
| entreeopleiding | 1,827 | 0,029 | 63,152 | <0,001 | 6,217 |
| niveau 2 | 0,604 | 0,018 | 33,344 | <0,001 | 1,829 |
| niveau 3 | 0,228 | 0,020 | 11,140 | <0,001 | 1,256 |
| Leeftijd | |||||
| referentiecategorie: t/m 16 jaar | |||||
| 17 jaar | 1,925 | 0,038 | 50,137 | <0,001 | 6,852 |
| 18 jaar | 1,874 | 0,039 | 48,116 | <0,001 | 6,512 |
| 19 jaar | 1,873 | 0,041 | 46,178 | <0,001 | 6,511 |
| 20 jaar | 2,015 | 0,043 | 46,721 | <0,001 | 7,504 |
| 21 jaar | 2,143 | 0,047 | 45,222 | <0,001 | 8,526 |
| 22 jaar | 2,152 | 0,053 | 40,264 | <0,001 | 8,601 |
| 23 jaar | 2,207 | 0,059 | 37,344 | <0,001 | 9,088 |
| 24 jaar | 2,110 | 0,067 | 31,317 | <0,001 | 8,245 |
| 25 jaar | 2,070 | 0,074 | 27,858 | <0,001 | 7,921 |
| 26 jaar | 2,018 | 0,082 | 24,721 | <0,001 | 7,521 |
| Problematische schulden | |||||
| referentiecategorie: student en huishouden zonder schulden | |||||
| student met schulden | 0,839 | 0,031 | 26,977 | <0,001 | 2,315 |
| huishouden met schulden | 0,383 | 0,021 | 18,280 | <0,001 | 1,467 |
| Ouderlijke structuur | |||||
| referentiecategorie: woont bij beide ouders | |||||
| woont bij 1 van de ouders (evt. + partner) | 0,405 | 0,016 | 24,946 | <0,001 | 1,499 |
| woont zonder ouders | 0,605 | 0,025 | 24,498 | <0,001 | 1,830 |
| Verdachte van een misdrijf | |||||
| referentiecategorie: niet | |||||
| wel | 0,847 | 0,028 | 30,725 | <0,001 | 2,333 |
| Geslacht | |||||
| referentiecategorie: man | |||||
| vrouw | -0,502 | 0,016 | -31,188 | <0,001 | 0,605 |
| Hoogst behaalde opleidingsniveau moeder | |||||
| referentiecategorie: middelbaar | |||||
| laag | 0,199 | 0,016 | 12,588 | <0,001 | 1,220 |
| hoog | -0,149 | 0,022 | -6,675 | <0,001 | 0,861 |
| onbekend | -0,424 | 0,042 | -9,974 | <0,001 | 0,655 |
| Stedelijkheid van de buurt | |||||
| referentiecategorie: niet stedelijk | |||||
| zeer sterk stedelijk | 0,374 | 0,025 | 14,703 | <0,001 | 1,454 |
| sterk stedelijk | 0,307 | 0,024 | 12,603 | <0,001 | 1,360 |
| matig stedelijk | 0,226 | 0,026 | 8,750 | <0,001 | 1,253 |
| weinig stedelijk | 0,120 | 0,027 | 4,406 | <0,001 | 1,127 |
| Leerweg | |||||
| referentiecategorie: BOL | |||||
| BBL | 0,469 | 0,020 | 23,139 | <0,001 | 1,599 |
| extranei | 0,533 | 0,044 | 12,173 | <0,001 | 1,704 |
| Studierichting | |||||
| referentiecategorie: zorg en maatschappij | |||||
| economisch en juridisch | 0,124 | 0,024 | 5,070 | <0,001 | 1,132 |
| technisch | -0,242 | 0,028 | -8,556 | <0,001 | 0,785 |
| landbouw, diergeneeskunde en -verzorging | -0,162 | 0,045 | -3,581 | <0,001 | 0,850 |
| overige richtingen | 0,043 | 0,023 | 1,866 | 0,062 | 1,044 |
| onbekend | -0,178 | 0,057 | -3,138 | 0,002 | 0,837 |
| Welvaartspercentiel | |||||
| referentiecategorie: 1 t/m 20 | |||||
| 21 t/m 40 | -0,090 | 0,020 | -4,451 | <0,001 | 0,914 |
| 41 t/m 60 | -0,165 | 0,022 | -7,428 | <0,001 | 0,848 |
| 61 t/m 80 | -0,314 | 0,025 | -12,499 | <0,001 | 0,731 |
| 81 t/m 100 | -0,413 | 0,030 | -13,949 | <0,001 | 0,662 |
| onbekend | 0,059 | 0,037 | 1,587 | 0,112 | 1,060 |
| Psychosociale problemen student | |||||
| referentiecategorie: geen | |||||
| wel | 0,514 | 0,035 | 14,553 | <0,001 | 1,672 |
| Uitkomst | Coëfficient | Standaardfout | Z-score | P-waarde | Odds ratio |
|---|---|---|---|---|---|
| Constante | -4,877 | 0,052 | -93,474 | <0,001 | 0,008 |
| Niveau | |||||
| referentiecategorie: niveau 4 | |||||
| entreeopleiding | 1,480 | 0,031 | 47,667 | <0,001 | 4,394 |
| niveau 2 | 0,537 | 0,019 | 27,923 | <0,001 | 1,710 |
| niveau 3 | 0,248 | 0,022 | 11,468 | <0,001 | 1,281 |
| Leeftijd | |||||
| referentiecategorie: t/m 16 jaar | |||||
| 17 jaar | 1,878 | 0,038 | 49,045 | <0,001 | 6,539 |
| 18 jaar | 1,759 | 0,039 | 45,272 | <0,001 | 5,808 |
| 19 jaar | 1,770 | 0,040 | 43,768 | <0,001 | 5,871 |
| 20 jaar | 1,883 | 0,043 | 43,511 | <0,001 | 6,571 |
| 21 jaar | 2,040 | 0,047 | 43,058 | <0,001 | 7,687 |
| Ouderlijke structuur | |||||
| referentiecategorie: woont bij beide ouders | |||||
| woont bij 1 van de ouders (evt. + partner) | 0,414 | 0,017 | 24,629 | <0,001 | 1,513 |
| woont zonder ouders | 0,713 | 0,027 | 26,474 | <0,001 | 2,039 |
| onbekend | 1,046 | 0,177 | 5,909 | <0,001 | 2,848 |
| Verdachte van een misdrijf | |||||
| referentiecategorie: niet | |||||
| wel | 0,901 | 0,029 | 31,218 | <0,001 | 2,462 |
| Problematische schulden | |||||
| referentiecategorie: student en huishouden zonder schulden | |||||
| student met schulden | 0,780 | 0,052 | 15,076 | <0,001 | 2,182 |
| huishouden met schulden | 0,388 | 0,021 | 18,441 | <0,001 | 1,474 |
| Geslacht | |||||
| referentiecategorie: man | |||||
| vrouw | -0,518 | 0,017 | -30,142 | <0,001 | 0,596 |
| Hoogst behaalde opleidingsniveau moeder | |||||
| referentiecategorie: middelbaar | |||||
| laag | 0,199 | 0,017 | 11,797 | <0,001 | 1,220 |
| hoog | -0,093 | 0,023 | -4,076 | <0,001 | 0,911 |
| onbekend | -0,651 | 0,050 | -12,988 | <0,001 | 0,522 |
| Welvaartspercentiel | |||||
| referentiecategorie: 1 t/m 20 | |||||
| 21 t/m 40 | -0,105 | 0,022 | -4,857 | <0,001 | 0,901 |
| 41 t/m 60 | -0,240 | 0,024 | -10,099 | <0,001 | 0,787 |
| 61 t/m 80 | -0,337 | 0,026 | -12,855 | <0,001 | 0,714 |
| 81 t/m 100 | -0,496 | 0,031 | -16,019 | <0,001 | 0,609 |
| onbekend | 0,056 | 0,040 | 1,380 | 0,168 | 1,057 |
| Leerweg | |||||
| referentiecategorie: BOL | |||||
| BBL | 0,504 | 0,021 | 23,533 | <0,001 | 1,655 |
| extranei | 0,515 | 0,054 | 9,547 | <0,001 | 1,674 |
| Studierichting | |||||
| referentiecategorie: zorg en maatschappij | |||||
| economisch en juridisch | 0,133 | 0,026 | 5,138 | <0,001 | 1,143 |
| technisch | -0,313 | 0,030 | -10,364 | <0,001 | 0,731 |
| landbouw, diergeneeskunde en -verzorging | -0,107 | 0,047 | -2,272 | 0,023 | 0,898 |
| overige richtingen | 0,023 | 0,024 | 0,961 | 0,337 | 1,024 |
| onbekend | -0,060 | 0,065 | -0,926 | 0,354 | 0,942 |
| Stedelijkheid van de buurt | |||||
| referentiecategorie: niet stedelijk | |||||
| zeer sterk stedelijk | 0,359 | 0,027 | 13,449 | <0,001 | 1,433 |
| sterk stedelijk | 0,306 | 0,025 | 12,010 | <0,001 | 1,358 |
| matig stedelijk | 0,218 | 0,027 | 8,075 | <0,001 | 1,244 |
| weinig stedelijk | 0,102 | 0,028 | 3,585 | <0,001 | 1,107 |
| Psychosociale problemen student | |||||
| referentiecategorie: geen | |||||
| wel | 0,571 | 0,041 | 14,094 | <0,001 | 1,771 |
Bijlage 6: Literatuur
A. Agresti (2013), Categorical Data Analysis (2e editie). John Wiley & Sons, New York.
D. McFadden (1974), Conditional logit analysis of qualitative choice behavior. In: P. Zarembka (ed.), Frontiers in Econometrics, Academic Press, pp. 105-142.
R.D. McKelvey & W. Zavoina (1975), A Statistical Model for the Analysis of Ordinal Level Dependent Variables. Journal of Mathematical Sociology, 4, 103–112.
J. Merlo, B. Chaix, H. Ohlsson, A. Beckman, K. Johnell, P. Hjerpe, L. Råstam & K. Larsen (2006), A Brief Conceptual Tutorial of Multilevel Analysis in Social Epidemiology: Using Measures of Clustering in Multilevel Logistic Regression to Investigate Contextual Phenomena. Journal of Epidemiology and Community Health, 60, 290–297.
D.B. Rubin (1987), Multiple Imputation for Nonresponse in Surveys. John Wiley & Sons, New York.
Bijlage 7: Privacy
Het CBS verzamelt gegevens van natuurlijke personen, bedrijven en instellingen. Dit is wettelijk vastgelegd in de CBS-wet en de Algemene Verordening Gegevensbescherming (AVG). Identificerende persoonskenmerken worden na ontvangst direct gepseudonimiseerd. Hierdoor kan het onderzoek alleen worden uitgevoerd op gegevens met een pseudosleutel. Bij publicatie zorgt het CBS er bovendien voor dat natuurlijke personen of bedrijven niet herkenbaar of herleidbaar zijn. Ook hanteert het CBS diverse maatregelen tegen diefstal, verlies of misbruik van persoonsgegevens. Het CBS levert geen herkenbare gegevens aan derden, ook niet aan andere overheidsinstellingen. Wel kunnen sommige (wetenschappelijke) instellingen onder strenge voorwaarden toegang krijgen tot gegevens met pseudosleutel op persoons- of bedrijfsniveau. Dit noemen we microdata.
Voor meer informatie, zie onze website: www.cbs.nl/privacy.